|
|
КСП для 8; 10 класса. Предел функции в точке и на бесконечности
Раздел:
|
|
ФИО педагога
|
Лаган Н.Д.
|
Дата:
|
|
Класс: 10 б
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Критические точки и точки экстремума
|
Цели обучения в соответствии
с учебной программой
|
10.3.1.16 - знать определения критических точек и точек экстремума функции, условие существования экстремума функции;
10.3.1.17 - находить критические точки и точки экстремума функции;
|
Цели урока
|
- знает определения критических точек и точек экстремума функции, условие существования экстремума функции;
-умеет находить критические точки и точки экстремума функции;
|
Ход урока
|
Этап урока/ Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
|
Организационный момент.
Создать благоприятный психологический настрой на работу, подготовка к уроку необходимых принадлежностей
|
Приготовиться к уроку, настроиться на работу
|
|
|
Середина урока
|
Задание на повторение.
№4 (а) с.4
Устная работа
Найдите производные функций.
а) y = 2x2+ x ;
б) f(x) = 3x2– 7x + 5;
в) f(x) =3х+12;
г) f(x) = 1/2x2;
д) f(x) = (2x – 5)(x + 3).
Изучение нового материала и отработки навыка применения.
Сегодня на уроке мы научимся определять критических точек и точки экстремума функции, узнаем условие существования экстремума функции.
Работа с п.20 с.110-113
1) определение критических точек;
2) определение экстремума функции;
3) алгоритм нахождения критических точек и точек экстремума функции.
Рассмотреть примеры на с.112
|
Выполняют краткий тезисный конспект в тетради,
работают с учебником;
|
|
учебник
|
Парная работа
|
№20.2
Используем алгоритм с.111
|
работа в парах, взаимопомощь
|
похвала учителя
взаимопроверка
|
|
Индивидуальная работа
|
№20.5(а,б)
Используем алгоритм с.111
|
работают самостоятельно
|
|
|
Конец урока
|
Рефлексия:
1.С какими новыми понятиями вы сегодня познакомились на уроке?
2.Довольны ли вы результатом? Что удивило или заинтересовало на уроке?
Домашнее задание №20.3(в,г)
|
Оценивают свою работу на уроке(самооценивание)
|
Оценка учителя.
|
|
Раздел:
|
|
ФИО педагога
|
Лаган Н.Д.
|
Дата: 22.02.22
|
|
Класс: 8в
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Решение текстовых задач. СОР
|
Цели обучения в соответствии
с учебной программой
|
8.4.2.3
использовать квадратичную функцию для решения прикладных задач;
|
Цели урока
|
используют квадратичную функцию для решения прикладных задач;
|
Ход урока
|
Этап урока/ Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
|
Организационный момент.
Создать благоприятный психологический настрой на работу, подготовка к уроку необходимых принадлежностей
|
Приготовиться к уроку, настроиться на работу
|
|
|
Середина урока
|
Проверка пройденной темы. С помощью метода «Толстые и тонкие вопросы» проверяет пройденную тему.
1)Какая функция называется квадратичной?
Выясните вверх или вниз направлены ветви параболы? у=4х2-5х+1 у=-3х2+6х-4 у=12х -5 х2-1 у= 7+8х+9х2
2)Не выполняя построения графика функции у=-3х2 -6х+1, ответьте на вопросы:
-Каковы координаты вершины параболы? (-1;4)
-Определите наибольшее или наименьшее значение имеет функция:
1) у=25х2- 30х +8
2) у=х2+ 4х+11
3) у = - 4х2+ 2х +1
4) у = 2 – 5х -3х2
-От чего зависит имеет ли функция свое наибольшее или наименьшее значение?
-Как определить направление ветвей параболы?
3)Алгоритм построения графика:
Найти координаты вершины параболы, отметить ее на координатной плоскости.
Провести ось симметрии параболы.
Найти нули функции, если они есть, и построить их на осиOx.
Построить еще несколько точек, принадлежащих параболе.
Провести через построенные точки параболу.
Задание на повторение :повторить алгоритм решения неравенства и решить неравенство.
4(x − 1) ≥ 5 + x
4x − 4 ≥ 5 + x
4x − x ≥ 5 + 4
3x ≥ 9 | (:3)
3x (:3) ≥ 9 (:3)
x ≥ 3
 Ответ: x ≥ 3 Ответ: x ≥ 3
|
Отвечают на вопросы
|
|
учебник
|
Парная работа
|
|
|
|
|
Индивидуальная работа
|
Выполнить СОР
|
Решают
|
|
карточки
|
Конец урока
|
Сдача работ.
|
|
|
|
Раздел:
|
|
ФИО педагога
|
Лаган Н.Д.
|
Дата:
|
|
Класс: 10 б
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Исследование функции с помощью производной и построение её графика
|
Цели обучения в соответствии
с учебной программой
|
10.3.1.18 - исследовать свойства функции с помощью производной и
строить её график;
|
Цели урока
|
исследуют свойства функции с помощью производной и
строят её график;
|
Ход урока
|
Этап урока/ Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
|
Организационный момент.
Создать благоприятный психологический настрой на работу, подготовка к уроку необходимых принадлежностей
|
Приготовиться к уроку, настроиться на работу
|
|
|
Середина урока
|
Задание на повторение.
№4 (а) с.4
Устная работа.Актуализация опорных знаний учащихся.
Повторить алгоритм с.115
Применение.
Исследуйте функцию f(x)= x3-3х2и постройте ее график
Решение:
Область определения данной функции - множество действительных чисел: D (f) =R.
Данная функция непрерывна на множестве действительных чисел как многочлен.
Найдем критические точки функции: f '(x)=3х2-6х = 3х (х-2),
f '(x)=0, 3х (х-2)=0, х=0 или х=2.
Составляем таблицу :
х
|
(-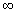 ; 0) ; 0)
|
0
|
(0; 2)
|
2
|
(2; 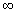 ) )
|
f ''(х)
|
+
|
0
|
-
|
0
|
+
|
f (х)
|
возрастает
|
0
|
убывает
|
-4
|
возрастает
|
|
|
max
|
|
min
|
|
Критические точки разбивают координатную прямую на три промежутка: (-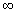 ; 0), (0; 2), (2; ; 0), (0; 2), (2; 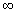 ). ).
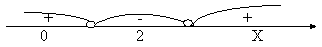
На рисунке указаны знаки производной f '(x) на каждом из этих промежутков.
Найдем нули функции: x3-3х2= 0, x2(х-3) = 0, x = 0 или x = 3.
Найдем координаты еще одной точки графика: если x =-1, то f (-1) = (-1)3- 3 * (-1)2= -4.
6) Строим график данной функции .
|
Отвечают на вопросы
|
|
учебник
|
Парная работа
|
№22.8
Используем алгоритм
|
работа в парах, взаимопомощь
|
похвала учителя
взаимопроверка
|
|
Индивидуальная работа
|
|
работают самостоятельно
|
|
|
Конец урока
|
Рефлексия:
1.С какими новыми понятиями вы сегодня познакомились на уроке?
2.Довольны ли вы результатом? Что удивило или заинтересовало на уроке?
Домашнее задание №22.10 б
|
Оценивают свою работу на уроке(самооценивание)
|
Оценка учителя.
|
|
Раздел:
|
|
ФИО педагога
|
Лаган Н.Д.
|
Дата:
|
|
Класс: 8в
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Площади четырёхугольников и треугольников
|
Цели обучения в соответствии
с учебной программой
|
8.1.3.13 выводить и применять формулы площади трапеции
|
Цели урока
|
Применяет формулу площади трапеции для решения задач
|
Ход урока
|
Этап урока/ Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
|
Начало урока
|
Организационный момент.
Создать благоприятный психологический настрой на работу, подготовка к уроку необходимых принадлежностей
|
Приготовиться к уроку, настроиться на работу
|
|
|
Середина урока
|
Повторение. с.40
1.Что называется трапецией?
2.Как называются стороны трапеции?
3.Какие виды трапеций вам известны?
4. Что известно про углы трапеции, которые прилегают к боковой стороне?
5. Что называется средней линией трапеции?
6. Чему равна средняя линия трапеции?
7. Что называется высотой трапеции?
Постановка проблемы.
Предложите пути решения задачи.
Стратегия: «Мозговой штурм».
Актовый зал школы имеет форму прямоугольной трапеции с основанием 20 м и 10 м высотой 8 м. Хватит ли 9 кг краски, чтобы покрасить пол актового зала, если расход краски составляет
1 кг/10 м2?

Учитель наблюдает за работой, отмечает достижения каждого.
Молодцы!
А можно ли вычислить площадь трапеции без деления её на части?
Как вы думаете, что мы сегодня узнаем и чему научимся?
Формула для вычисления площади трапеции.
Площадь трапеции равна произведению полусуммы длин оснований на высоту.

|
Отвечают на вопросы
Чертят прямоугольную трапецию, вычисляют площадь
Дескрипторы:
-выполнен чертёж прямоугольной трапеции
-отмечены измерения
-разделение на прямоугольник и треугольник
-вычислена площадь прямоугольника
-вычислена площадь треугольника
-вычислена площадь трапеции
-вычислено необходимое количество краски
- записан(дан) ответ
|
|
|
Парная работа
|
Решение задач.
Уровень А с.103
|
работа в парах, взаимопомощь
|
похвала учителя
взаимопроверка
|
|
Индивидуальная работа
|
|
работают самостоятельно
|
|
|
Конец урока
|
Рефлексия:
1.С какими новыми понятиями вы сегодня познакомились на уроке?
2.Довольны ли вы результатом? Что удивило или заинтересовало на уроке?
Домашнее задание №6 с.103 выучить формулу
|
Оценивают свою работу на уроке(самооценивание)
|
Оценка учителя.
|
|
Раздел:
|
10.3А Угол в пространстве. Расстояние в пространстве
|
ФИО педагога
|
Лаган Н.Д.
|
Дата
|
|
Класс: 10 б
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Расстояние между двумя точками
|
Цели обучения в соответствии
с учебной программой
|
10.4.2 - уметь находить расстояние между двумя точками в пространстве;
|
Цели урока
|
находят расстояние между двумя точками в пространстве;
|
Ход урока
|
Этап урока/ Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
|
Организационный момент.
Создать благоприятный психологический настрой на работу, подготовка к уроку необходимых принадлежностей
|
Приготовиться к уроку, настроиться на работу
|
|
|
Середина урока
|
Актуализация опорных знаний. Повторить
Расстояние между точками на плоскости;
Деление отрезка пополам на плоскости.
Применить к пространству
|
работают с учебником;
|
|
учебник
|
Парная работа
|
|
работа в парах, взаимопомощь
|
похвала учителя
взаимопроверка
|
|
Индивидуальная работа
|
|
работают самостоятельно
|
|
|
Рефлекция
|
Рефлексия:
1.С какими новыми понятиями вы сегодня познакомились на уроке?
2.Довольны ли вы результатом? Что удивило или заинтересовало на уроке?
|
Обобщают изученный материал.
Делают вывод.
Оценивают свою работу на уроке(самооценивание) о
|
Оценка учителя.
|
|
Домашнее задание
|
|
Записывают в дневники домашнее задание.
|
|
|
Раздел:
|
|
ФИО педагога
|
Лаган Н.Д.
|
Дата:
|
|
Класс: 10 а
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Правила нахождения производных
|
Цели обучения в соответствии
с учебной программой
|
10.4.1.21 - знать и применять правила дифференцирования;
|
Цели урока
|
находит производные постоянной функции и степенной функции; применяет правила дифференцирования;
|
Ход урока
|
Этап урока/ Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
|
Организационный момент.
Создать благоприятный психологический настрой на работу, подготовка к уроку необходимых принадлежностей
|
Приготовиться к уроку, настроиться на работу
|
|
|
Середина урока
|
Устная работа
Дайте определение производной функции.
Что такое приращение аргумента, приращение функции?
Как называют функцию, имеющую производную в некоторой точке?
Как называется процесс вычисления производной?
Изучение темы. п.41 с.67-69
Правила нахождения производных
Производная суммы равна сумме производных
(u + v)`= u` + v`
Производная произведения равна
(u • v)`= u`v + u v`
Следствие из второго правила
Постоянный множитель можно выносить за знак производной
(Cu)`= Cu`
Производная частного равна
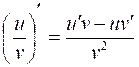
Производная степенной функции
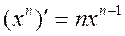
Устно.
Найти производные следующих функций:
а) y=x5+9x20+1;
б) y=x7-4x16-3;
в) y=x2-15x+6;
|
Выполняют краткий тезисный конспект в тетради,
работают с учебником;
|
|
учебник
|
Парная работа
|
№41.2(4,5)
|
работа в парах, взаимопомощь
|
похвала учителя
взаимопроверка
|
|
Индивидуальная работа
|
Найдите производную функции: 1)f(x)= 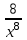 +12 +12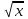
2) у=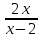 -12 -12
|
работают самостоятельно
|
|
|
Конец урока
|
Рефлексия:
1.С какими новыми понятиями вы сегодня познакомились на уроке?
2.Довольны ли вы результатом? Что удивило или заинтересовало на уроке?
Домашнее задание №41.9(1,2)
|
Оценивают свою работу на уроке(самооценивание)
|
Оценка учителя.
|
|
Раздел:
|
|
ФИО педагога
|
Лаган Н.Д.
|
Дата:
|
|
Класс: 10 б
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Наибольшее и наименьшее значения функции на отрезке
|
Цели обучения в соответствии
с учебной программой
|
10.3.1.19 - находить наибольшее и наименьшее значения функции на отрезке;
10.3.3.3 - решать прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции;
|
Цели урока
|
- находит наибольшее и наименьшее значения функции на отрезке;
- решает прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции;
|
Ход урока
|
Этап урока/ Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
|
Организационный момент.
Создать благоприятный психологический настрой на работу, подготовка к уроку необходимых принадлежностей
|
Приготовиться к уроку, настроиться на работу
|
|
|
Середина урока
|
Устная работа
Дайте определение производной функции.
Что такое приращение аргумента, приращение функции?
Как называют функцию, имеющую производную в некоторой точке?
Как называется процесс вычисления производной?
Найти производные следующих функций:
а) y=x5+9x20+1;
б) y=x7-4x16-3;
в) y=x2-15x+6;
Изучение темы. п.22 с.118-120
Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции у=f(x) на отрезке [a;b]
1. Найти производную f`(x)
2. Найти стационарные и критические точки функции, лежащие внутри отрезка [a;b]
3. Вычислить значения функции у=f(x) в точках, отобранных на втором шаге, и в точках a и b выбрать среди этих значений наименьшее ( это будет Унаим.) и наибольшее (это будет Унаиб.).
Пошагово разобрать примеры из учебника.
|
Выполняют краткий тезисный конспект в тетради,
работают с учебником;
|
|
учебник
|
Парная работа
|
№22.1-22.3
Используем алгоритм
|
работа в парах, взаимопомощь
|
похвала учителя
взаимопроверка
|
|
Индивидуальная работа
|
Найдите производную функции: 1)f(x)= 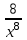 +12 +12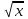
2) у=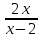 -12 -12
|
работают самостоятельно
|
|
|
Конец урока
|
Рефлексия:
1.С какими новыми понятиями вы сегодня познакомились на уроке?
2.Довольны ли вы результатом? Что удивило или заинтересовало на уроке?
Домашнее задание №22.7
|
Оценивают свою работу на уроке(самооценивание)
|
Оценка учителя.
|
|
Раздел:
|
|
ФИО педагога
|
Лаган Н.Д.
|
Дата:
|
|
Класс: 8в
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Полигон частот, гистограмма частот
|
Цели обучения в соответствии
с учебной программой
|
8.3.3.1представлять результаты выборки в виде интервальной таблицы частот;
8.3.3.2представлять данные интервальной таблицы частот в виде гистограммы частот;
8.3.3.3знать определение накопленной частоты;
|
Цели урока
|
-представляет результаты выборки в виде интервальной таблицы частот;
-представляет данные интервальной таблицы частот в виде гистограммы частот;
-знает определение накопленной частоты;
|
Ход урока
|
Этап урока/ Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
|
Организационный момент.
Создать благоприятный психологический настрой на работу, подготовка к уроку необходимых принадлежностей
Мотивация:
Поднимите руки те, кто знает математику;
Поднимите руки те, кто любит математику;
Поднимите руки те, кто хочет знать математику;
Постановка цели и плана урока, учитель озвучивает критерии оценивания, определяет «зону ближайшего развития» учащихся, ожидания к концу урока.
|
Приготовиться к уроку, настроиться на работу
|
|
|
Середина урока
|
Статистика — это раздел математики в котором изучаются вопросы сбора, измерения и анализа информации, представленной в числовой форме. Происходит слово статистика от латинского слова status (состояние или положение дел).
Так, с помощью статистики мы можем узнать свое положение дел, касающихся финансов. С начала месяца можно вести дневник расходов и по окончании месяца, воспользовавшись статистикой, узнать сколько денег в среднем мы тратили каждый день или какая потраченная сумма была наибольшей в этом месяце либо узнать какую сумму мы тратили наиболее часто.
На основе этой информации можно провести анализ и сделать определенные выводы: следует ли в следующем месяце немного сбавить аппетит, чтобы тратить меньше денег, либо наоборот позволить себе не только хлеб с водой, но и колбасу.
Повторить следующие понятия:
Выборка. Объем. Размах
Среднее арифметическое
Мода и медиана
Частота
Относительная частота
С этой целью учащимся необходимо выполнить задание, обсуждая решение со всем классом, тем самым учащиеся повторят выше указанные понятия.
Среди учащихся восьмого класса проведен опрос о том, из скольки человек состоит их семья. В результате опроса была получена следующая выборка: 4, 4, 5, 5, 6, 6, 4, 3, 7, 7, 2, 3, 6, 3 ,4, 2, 7, 4, 5, 4, 3, 3, 2, 4, 5.
Каждое число в выборке означает количество человек в семье каждого опрошенного учащегося. Представьте данную выборку в виде частотной таблицы.
Количество человек в семье
|
2
|
3
|
4
|
5
|
6
|
7
|
Абсолютная частота
|
|
|
|
|
|
|
Относительная частота
|
|
|
|
|
|
|
После того, как учащиеся заполнят таблицу, учитель предлагает им найти среднее арифметическое, моду, медиану числового ряда.
|
Выполняют краткий тезисный конспект в тетради,
работают с учебником;
|
|
учебник
|
Парная работа
|
№ 15.4
Критерии оценивания
верно записывает интервалы;
представляет данные в виде интервальной таблицы.
|
работа в парах, взаимопомощь
|
похвала учителя
взаимопроверка
|
|
Индивидуальная работа
|
|
работают самостоятельно
|
|
|
Конец урока
|
Рефлексия:
1.С какими новыми понятиями вы сегодня познакомились на уроке?
2.Довольны ли вы результатом? Что удивило или заинтересовало на уроке?
Домашнее задание №15.6
|
Оценивают свою работу на уроке(самооценивание)
|
Оценка учителя.
|
| |
|
|
 Скачать 437.19 Kb.
Скачать 437.19 Kb.