Предмет математика. Счёт предметов. Один, два, три порядковые числительные первый, второй, третий
 Скачать 2.59 Mb. Скачать 2.59 Mb.
|
|
Тема: Закрепление и обобщение знаний ПО ТЕМЕ «ЧИСЛА 1–5. СОСТАВ ЧИСЕЛ 2–5» Педагогические цели: проверить знание состава изученных чисел, навык прямого и обратного счёта (от 1 до 5, от 5 до 1); учить чертить многоугольники по линейке, пользоваться линейкой. Планируемые результаты (предметные): знать состав изученных чисел; уметь выполнять прямой и обратный счёт (от 1 до 5, от 5 до 1); различать многоугольники, чертить многоугольники по линейке, пользоваться линейкой. Универсальные учебные действия (метапредметные): Регулятивные: уметь самостоятельно ставить цель предстоящей практической работы, планировать способы достижения поставленной учебной (практической) задачи и оценивать результат своей работы. Коммуникативные: уметь рассуждать и анализировать условие задания. Познавательные: стремиться к расширению своей познавательной сферы, стараться производить логические мыслительные операции (анализ, сравнение) для решения познавательной задачи. Личностные:проявляют основы самоорганизации – организации исследовательского пространства ученика. Сценарий урока I. Закрепление и обобщение знаний учащихся о числах 1–5 и составе чисел 2–5. 1. Игра «Путаница». На доске (или наборном полотне) записаны числа: 4 1 3 2 5 – Что заметили? Расположите числа по порядку. Учащиеся могут расположить числа двумя способами. (1 2 3 4 5; 5 4 3 2 1.) – Как называется порядок, когда числа расположены от меньшего к большему? – Порядок увеличения можно назвать и по-другому: порядок возрастания. Порядок, в котором числа расположены от большего к меньшему, называется порядком уменьшения. Данный порядок можно назвать и по-другому: порядок убывания. 2. Игра «Назови соседа». 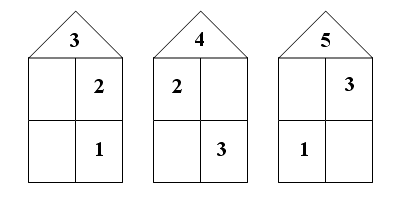 Данная игра позволяет учителю проверить, как учащиеся усвоили состав изученных чисел, а ученикам – закрепить знание состава этих чисел.  3. Упражнение в умении соотносить число и цифру. Работа в тетради (с. 14). – Рассмотрите задания 1, 2, 3. – Как вы думаете, какую работу необходимо выполнить в данных заданиях? (В задании 1 записать соответствующей цифрой количество изображённых предметов, в задании 2 для каждого рисунка найти свою схему и запись, в задании 3 нарисовать такое количество фигур, которое соответствует написанной цифре). Самостоятельная работа учащихся. Взаимопроверка.  II. Фронтальная работа по учебнику (с. 38–39). III. Пропедевтика темы «Задача» (задание 1, с. 51 учебника). Учащиеся, выполняя задание, по рисункам составляют краткие рассказы, содержащие вопрос, и соотносят числовые выражения с рисунками и составленными рассказами. IV. Итог урока. Вопросы: Что нового узнали на уроке? Как оцениваете свою работу на уроке? Урок 18 Тема: ТОЧКА. КРИВАЯ ЛИНИЯ. ПРЯМАЯ ЛИНИЯ. ОТРЕЗОК Педагогические цели: дать первичные представления о кривой и прямой линиях, отрезке; продолжить работу по усвоению состава чисел 2–5; учить чертить геометрические фигуры по линейке, правильно пользоваться линейкой; прививать аккуратность. Планируемые результаты (предметные): уметь распознавать геометрические фигуры: точку, кривую и прямую линии, отрезок; знать состав чисел 2–5. Универсальные учебные действия (метапредметные): Регулятивные:уметь организовывать своё рабочее место под руководством учителя; определять цель выполнения заданий на уроке, во внеурочной деятельности, в жизненных ситуациях под руководством учителя; определять план выполнения заданий на уроках, внеурочной деятельности, жизненных ситуациях под руководством учителя; использовать в своей деятельности простейшие приборы: линейку, треугольник и т. д. Коммуникативные: уметь с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации. Познавательные: уметь моделировать – преобразовывать объекты из чувственной формы в модели, где выделены существенные характеристики объекта (пространственно-графическая или знаково-символическая); преобразовывать модели с целью выявления общих законов, определяющих данную предметную область. Личностные:обеспечивают ценностно-смысловую ориентацию в отношении к школе, учению и поведению в процессе учебной деятельности; соблюдают организованность, дисциплинированность на уроке, действуют согласно памятке обращения с учебными пособиями, наглядным и счётным материалами, инструментами для построения геометрических фигур и правил работы. Сценарий урока I. Изучение нового материала. 1. Знакомство с новыми понятиями. На доске изображено несколько разных линий. 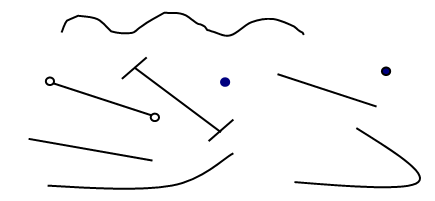 – Посмотрите на доску и скажите, что заметили. – Разделите все изображённые на доске объекты на 4 группы. (Точки, кривые линии, прямые линии, отрезки.) 2. Графическое изображение изученных линий. Выводы. – Чем прямая линия отличается от кривой? Каким чертёжным инструментом нужно воспользоваться, чтобы начертить прямую линию? (Линейкой.) – Как вы думаете, почему линейку так назвали? – Про линейку даже есть стихотворение: Я – линейка, Прямота – моя главная черта. – Начертите в ваших тетрадях одну прямую линию и одну кривую. – Нужна ли линейка, для того чтобы начертить кривую линию? – Поставьте в ваших тетрадях точку. – Как вы думаете, сколько прямых линий можно провести через одну точку? – Проведите одну прямую линию. – Можно ли провести ещё? Проведите. – А ещё можно провести прямую линию через эту же точку? Проведите. – А ещё можно? Проведите. – Какой вывод можно сделать? (Через одну точку можно провести бесконечно много прямых линий.) – Как вы думаете, можно ли через одну точку провести бесконечно много кривых линий? – Попробуйте это сделать. Какой вывод из этого следует? – А теперь поставьте в ваших тетрадях две точки. Сколько через них можно провести прямых линий? – Проведите прямую линию. – Проведите ещё одну прямую через эти же точки. (Пытаются выполнить задание и приходят к выводу, что это сделать невозможно.) – Получилось ли у вас это сделать? Какой вывод из этого следует? (Через две точки можно провести только одну прямую линию.) – Поставьте ещё две точки в ваших тетрадях. – Сколько кривых можно провести через них? – Проведите одну кривую линию. – Можно ли провести ещё одну кривую линию через эти же две точки? Попробуйте это сделать. – А ещё одну? Проведите. – Какой вывод из этого следует? (Через две точки можно провести много кривых линий.) – Проведите прямую линию. Поставьте на ней две точки. – Часть прямой от одной точки до другой выделите цветным карандашом. – Посмотрите внимательно на доску и найдите линии, похожие на полученную вами. – Как называются эти линии? (Отрезки.) – Чем отрезок отличается от прямой линии? Вывод: отрезок – это часть прямой линии. Отрезок имеет начало и конец, то есть ограничен с двух сторон точками, в отличие от прямой линии, которая не имеет ни начала, ни конца, то есть бесконечна. – Начертите в ваших тетрадях два отрезка. Взаимопроверка.  II. Пропедевтика темы «Задача» (задание 2, с. 41 учебника). – Как вы думаете, какое задание предстоит выполнить? – Составьте рассказы и поставьте к ним вопросы. – Какое числовое выражение соответствует первому (второму) рисунку? – Какие числовые выражения оказались «лишними»? – Составьте по ним рассказы.  III. Составление и чтение равенств. Работа по учебнику (задание 3, с. 41). – Составьте выражения в соответствии с рисунками. Выражения могут записываться учащимися в тетрадях с комментированием, а могут быть записаны только на доске. –Прочитайте выражения разными способами. Работа в тетради (задание 1, с. 15). Дано выражение: 3 + 2 = 5. Учащиеся закрашивают 3 квадрата синим цветом, а 2 квадрата – зелёным. Вся работа выполняется фронтально. IV. Итог урока. Вопросы: Какие открытия сделали? Какая линия называется прямой? Что такое «отрезок»? Сколько прямых линий можно провести через одну точку? А через две? Урок 19 Тема: ЛОМАНАЯ ЛИНИЯ. ЗВЕНО ЛОМАНОЙ Педагогические цели: создать условия для усвоения понятий «ломаная линия», «звено ломаной»; формирования первичных представлений о ломаной; учить чертить ломаные линии по линейке, правильно пользоваться линейкой; прививать аккуратность. Планируемые результаты (предметные): знать понятия «ломаная линия», «звено ломаной»; уметь чертить ломаные линии. Универсальные учебные действия (метапредметные): Регулятивные: уметьразличать способ и результат действия, принимать и выполнять практической задачи. Коммуникативные:уметь доносить свою позицию до других: оформлять свою мысль в устной (на уровне одного предложения или небольшого текста); слушать и понимать речь других; демонстрировать своё понимание высказывания партнера по общению. Познавательные: уметь разделять объекты (модели) на составные части в практической деятельности, соединять различные элементы, стороны объектов в единое целое в практической деятельности. Личностные:устанавливают связи между целью учебной деятельности и её мотивом, другими словами, между результатом учения и тем, что побуждает к деятельности, ради чего она осуществляется; умеют задавать себе вопрос: какое значение и какой смысл имеет для меня учение? – и отвечать на него. Сценарий урока I. Закрепление и повторение изученного о прямой линии, отрезке, кривой линии. Данную работу можно провести по рисункам в заданиях на с. 42, 43 учебника либо по рисункам, подобранным учителем. – Покажите на рисунках прямые линии. Докажите, что это прямые линии. – Найдите на рисунках отрезки. Обоснуйте ваше мнение. – Какие линии – кривые? Почему так считаете? II. Изучение нового материала. 1. Знакомство с новыми понятиями. На доске изображены различные линии:  – Что хотите сказать? – На какие группы можно разделить данные линии? Как бы вы их назвали? – Такая линия называется ломаной. Учитель может также продемонстрировать учащимся наглядно, как из прямой линии получить ломаную. – Рассмотрите несколько ломаных линий. Что заметили? – Из каких линий состоят ломаные? (Из отрезков.) – Каждый такой отрезок (часть ломаной) – звено ломаной. Работа с учебником (с. 42). – Сравните две группы линий на рисунках, данные на полях учебника. Что увидели? – Ломаные линии на первом рисунке называются незамкнутыми, а ломаные на втором рисунке – замкнутыми линиями.  2. Формирование умения выполнять чертежи по линейке. Работа в тетради (заданиям 2, 3, с. 16 – 17). – Соедините данные в заданиях точки линиями. Учитель оказывает индивидуальную помощь детям. – Что получилось? (Ломаные.) – Есть ли среди данных ломаных замкнутые ломаные? А незамкнутые? Покажите их. – Сколько звеньев в первой ломаной (во второй, в третьей)? III. Составление и чтение равенств. Работа ведётся по заданию 1 (с. 16 тетради). – Рассмотрите рисунки. Составьте равенства, соответствующие рисункам. (Дано 5 квадратов, 2 из них зачёркнуто, значит, было 5, из 5 вычли 2, осталось 3, получаем равенство 5 – 2 = 3.) Аналогичная работа проводится с заданием учебника.  Самостоятельная работа с использованием счётного материала. – Решите равенства, данные в задании 3 (с. 43 учебника). IV. Фронтальная проверка и самопроверка. Один из учащихся читает равенства, называя полученный ответ. Ученики могут это делать по очереди, остальные ученики, если у них такой же (правильный) ответ, ставят около него «плюс» карандашом. V. Пропедевтика темы «Задача». По рисункам, данным в задании 1 (с. 43 учебника), учащиеся составляют короткие (математические) рассказы, содержащие вопрос, и подбирают равенства, соответствующие каждому рассказу. Найдя лишнее равенство, ученики придумывают по нему рассказ. VI. Итог урока. Вопросы: Чему учились на уроке? Что нового узнали? Что такое «звено ломаной»? Как вы работали на уроке? Урок 20 Тема: СОСТАВ ЧИСЕЛ 2–5 Педагогические цели: создать условия для закрепления навыков счёта от 1 до 5 и от 5 до 1; развития умения получать изученные числа разными способами; закрепления знаний об отрезке, прямой линии, ломаной; продолжить работу по составлению и чтению равенств, подготовительную работу к изучению темы «Задача»; прививать аккуратность. Планируемые результаты (предметные): знать состав чисел 2–5; уметь считать от 1 до 5 и от 5 до 1; производить классификацию предметов, математических объектов по одному основанию (цвет, форма, размер, материал); выбирать единицу измерения для данной величины. Универсальные учебные действия (метапредметные): Регулятивные:уметь выполнять оценку – выделение и осознание того, что уже усвоено и что ещё нужно усвоить, осознание качества и уровня усвоения; оценку результатов работы; проявлять саморегуляцию как способность к мобилизации сил и энергии, к волевому усилию (к выбору в ситуации мотивационного конфликта) и преодолению препятствий. Коммуникативные: Уметь с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации. Познавательные: уметь самостоятельно выделять и формулировать познавательную цель, делать умозаключения и выводы в словесной форме. Личностные:стремятся к повышению культуры речевого общения, к овладению приёмами творческого самовыражения с осознанием общественной полезности своего труда и своей жизни в целом; стараются проявить по назначению приобретённые математические способности. Сценарий урока I. Работа над составом чисел 2–5. 1. Составление и чтение равенств. – Предлагаю «сходить» в магазин игрушек. Помогут в этом рисунки из задания 1 (с. 45 учебника). – Пользуясь рисунками и схемами, составьте равенства и запишите их на доске. «Записывают» равенства цифрами и знаками кассы цифр. На доске: 4 – 1 = 3 4 + 1 = 5 4 – 2 = 2 3 + 2 = 5 4 – 3 = 1 2 + 3 = 5 1 + 4 = 5 – Рассмотрите рисунки из геометрических фигур и составьте по ним равенства. Полученные равенства запишите в тетрадях с комментированием. Запись в тетради: 4 – 2 = 2 4 + 1 = 5  2. Игра «Домино». Учащиеся под руководством учителя сначала разбирают задание 2 (с. 44 учебника), проговаривая хором состав записанных чисел: «Три – это два и один. Три – это один и два. Пять – это четыре и один. Пять – это один и четыре. Пять – это три и два. Пять – это два и три». Затем учащиеся выполняют задание 2 (поля с. 45 учебника) : самостоятельно вставляют пропущенное число, пользуясь кубиком «домино». Данная работа проводится фронтально. Так же, как и в предыдущем задании, учащиеся проговаривают хором состав чисел, предварительно вставив нужное число. II. Закрепление навыков счёта. Работа в тетради (задание 4, с. 17). – Посчитав количество предметов в каждой рамке, соедините линией каждую рамку с соответствующей цифрой. После этого задания учащиеся прописывают числа от 1 до 5 и от 5 до 1 в порядке увеличения и в порядке уменьшения (задание 5, с. 16). Взаимопроверка.  III. Пропедевтика темы «Задача». По рисункам задания 1 (с. 44 учебника) учащиеся составляют короткие (математические) рассказы, содержащие вопрос, подбирают из равенств, записанных ниже, соответствующие рассказам и рисункам, а к оставшимся равенствам придумывают свои рассказы. IV. Работа с геометрическим материалом (задание 3, с. 45 учебника). Данное задание лучше вынести на доску. – Рассмотрите рисунки. Что хотите сказать? – Как называются линии на первом рисунке? – Можно ли про линии на втором рисунке сказать, что они тоже ломаные? Почему? – Сколько звеньев в первой ломаной? А во второй? – Сколько всего отрезков изображено на втором рисунке? – Сравните длины отрезков при помощи данной в учебнике мерки. – Что можно сказать о длине отрезков? – Как вы узнали, что зелёный отрезок длиннее розового? (Зелёный отрезок длиннее розового, так как в нём помещается 4 мерки, а в розовом 3; 4 больше 3, значит, зелёный отрезок длиннее.) V. Итог урока. Вопросы: Чему научились на уроке? Какими знаниями, приобретёнными сегодня, вам бы хотелось поделиться с друзьями, со старшими? Урок 21 |
