Лекции по теории автоматов. Прикладная теория цифровых автоматов. Методы анализа и синтеза комбинационных схем
 Скачать 3.39 Mb. Скачать 3.39 Mb.
|
2.
1, a6
2, a4
2, a2 |
| am | K(am) | as(Y) | K(as) | X | ФВ |
| a6 | 110 | a1(-) | 001 | x4 | D3 |
| a7 | 100 | | | 1 | D3 |
 a1 a1 | 001 | a2(y1y2) | 000 | x1 | - |
 a2 a2 | 000 | | | x3x2 | |
| a6 | 110 | | | x4  | |
| a1 | 001 | a3(y3y4) | 010 | x1 | D2 |
| a4 | 011 | | | 1 | D2 |
| a3 | 010 | a4(y1y4) | 011 | x2 | D2D3 |
| a2 | 000 | a5(y2y3) | 101 | x3  | D1D3 |
| a2 | 000 | a6(y4) | 110 | x3x2 | D1D2 |
| a3 | 010 | a7(y2) | 100 | x2  | D1 |
| a5 | 101 | | | 1 | D1 |
Построение таблицы выполняется аналогично автомату Мили.
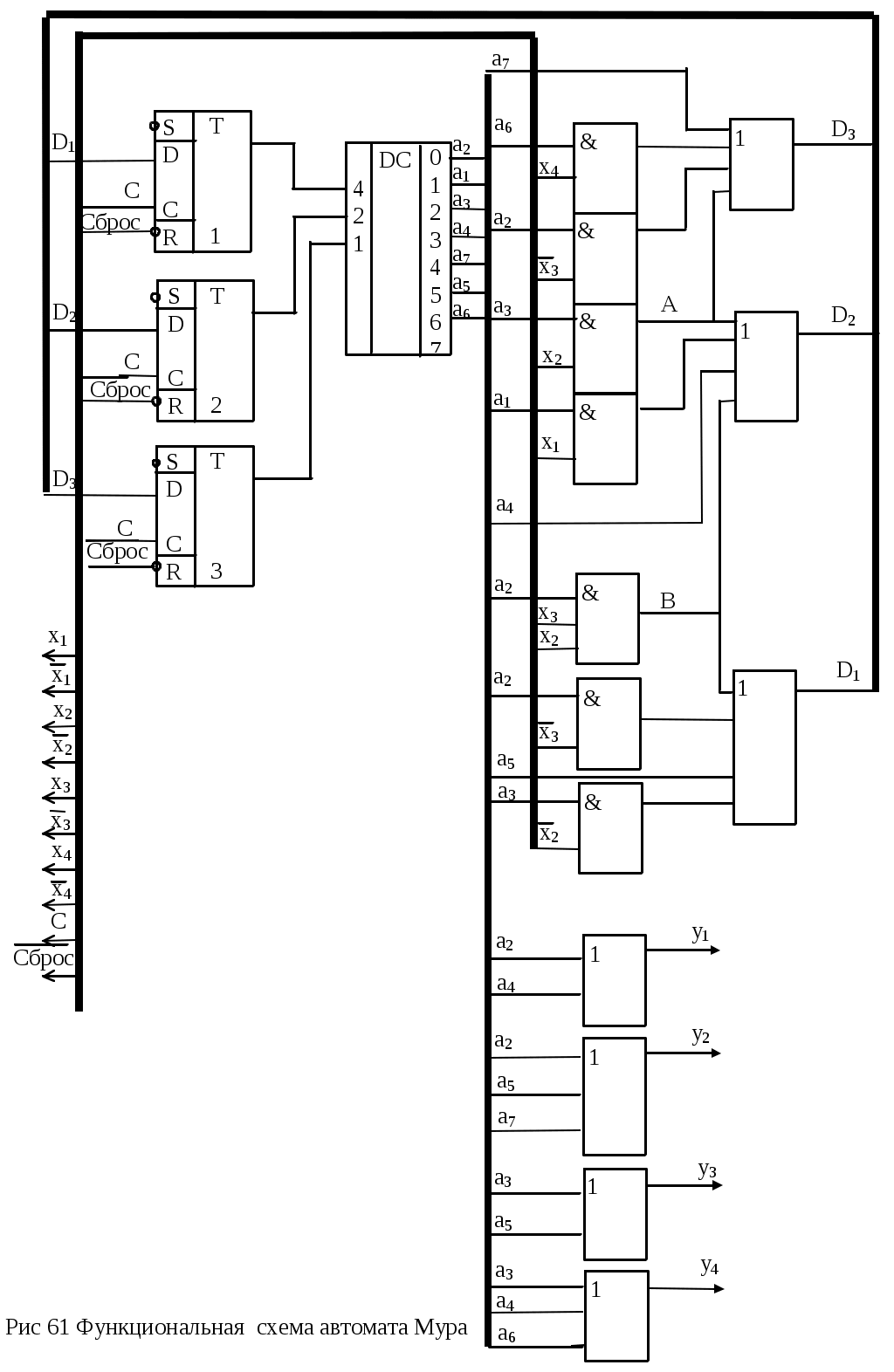
4. Выражения для функций возбуждения получаются в виде суммы произведений aiх, где ai-исходное состояние, х - условие перехода.
D

 1 = a2x3 + a2x3x2 + a3x2 + a5
1 = a2x3 + a2x3x2 + a3x2 + a5D2 = a1x1 + a4 + a3x2 + a2x3x2
D
 3 = a6x4 + a7 + a3x2 + a2x3
3 = a6x4 + a7 + a3x2 + a2x3или
A = a3x2
B = a2x3x2
D

 1 = a2x3 + B + a3x2 + a5
1 = a2x3 + B + a3x2 + a5D2 = a1x1 + a4 + A + B
D
 3 = a6x4 + a7 + A + a2x3
3 = a6x4 + a7 + A + a2x35. Выражения для выходных сигналов автомата Мура получаем, исходя из того, что эти сигналы определяются только внутренним состоянием автомата.
y1 = a2 + a4
y2 = a2 + a5 + a7
y3 = a3 + a5
y4 = a3 + a4 + a6
6. Для построения функциональной схемы автомата как и в предыдущем случае используем дешифратор состояний. Схема представлена на рис. 61 .
ЗАМЕЧАНИЯ.
1. При синтезе микропрограммных автоматов изложенным методом получаемые выражения для функций возбуждения не всегда являются минимальными и в некоторых случаях могут быть упрощены. В частности, можно доопределить функции возбуждения на некоторых наборах единичным значением (а не нулевым, как было ранее) и выполнить все операции склеивания. Например, в синтезированном ранее автомате Мили таким образом можно получить значение k1=1. Рекомендуется в этом убедиться самостоятельно.
Для упрощения схем автоматов можно также предварительно упростить ГСА, уменьшив количество вершин или узлов методами, изложенными в / /.
Автомат Мили в течении такта сохраняет свое состояние и лишь в конце его переходит в новое. Пока автомат находится в данном состоянии Ai он вырабатывает выходные сигналы y=f(Ai,x), где х - сигналы, подаваемые на вход автомата в течение данного такта. В связи с этим автомат Мили может интерпретировать микропрограмму корректно только в том случае, если для любого перехода выполняется условие независимости логических условий от результатов выполнения микроопераций на данном переходе.
Условие независимости нарушается, если на некотором переходе из аm в аs под действием сигнала х с выработкой уi наблюдается функциональная зависимость х = f(уi). В таком случае выполнение микрооперации уi может привести к изменению значения х и автомат, находясь в состоянии аm, и, реагируя на набор входных сигналов, сформирует набор выходных сигналов, не соответствующий микропрограмме. Чтобы избежать этого, можно использовать следующие способы:
1) запомнить значение сигналов х на промежуток времени, равный длительности такта;
2) ввести в автомат дополнительные состояния;
3) реализовать автомат по схеме Мура.
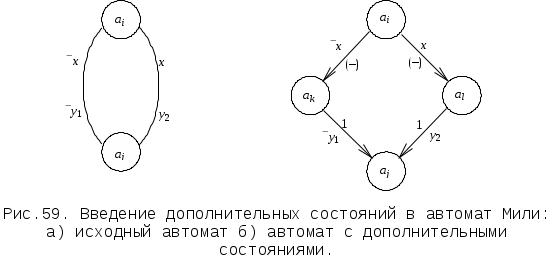
Запоминание значений сигналов х в течение такта осуществляется операционным автоматом с помощью дополнительных элементов памяти – триггеров. Интерпретация микропрограммы автоматом Мура рассматривалась ранее. Введение дополнительных состояний иллюстрируется рис. 59 .
В исходном автомате (рис. 59.а) есть переходы из аi в аj под действием сигналов х и х с выработкой y1 и y2 соответственно и имеет место х = f(y1, y2). Действительно, введение вспомогательных состояний аk и аl позволяет устранить возможную ошибку в выдаче выходных сигналов. На переходах аi аk или аiаl выходные сигналы не вырабатываются. Переходы аi аk или аiаl являются безусловными с выработкой y1 или y2 соответственно. В таком случае изменение значения х, в результате выполнения микроопераций y1 или y2, не повлияет на выходной сигнал, вырабатываемый автоматом, так как на переходах аi аk или аiаl выходной сигнал уже не зависит от х.
Синтез управляющего автомата Мура
на базе регистра сдвига.
Кроме рассмотренного ранее канонического метода, существуют и другие методы синтеза управляющих автоматов, среди которых наиболее широко используется синтез на базе регистра сдвига. Этот метод позволяет при построении схемы отказаться от дешифратора, т.к. состояния кодируются унитарным кодом. В автомате количество элементов памяти выбирается равным количеству внутренних состояний. В каждый момент времени только один триггер находится в 1, остальные в 0. Обычно при синтезе на базе регистра сдвига используются D-триггеры. Очень эффективен данный метод для так называемых линейных микропрограмм, т.е. микропрограмм без ветвлений (отсутствует логические условия). Рассмотрим пример синтеза управляющего автомата Мура данным методом. Пусть закодированная ГСА микропрограммы имеет вид рис. 60. Разметив данную ГСА для автомата Мура, получаем семь состояний. Следовательно число триггеров m=7. Выполним синтез с использованием D-триггеров. Закодируем состояния унитарным кодом: a1=1000000, a2=0100000,..., a7=0000001. Обратная структурная таблица переходов-выходов для данного автомата представлена в таблице.
-
am
Kam
as(y)
Kas
x
ФВ
а6
0000010
а1(-)
1000000
1
D1
а7
0000001
1
D1
а1
1000000
а2(y1 y2)
0100000
1
D2
а2
0100000
а3( y2)
0010000
1
D3
а3
0010000
а4(y3 y4)
0001000
1
D4
а4
0001000
а5( y2)
0000100
D5
а5
0000100
а6(y3)
0000010
1
D6
а4
0001000
а7(y4)
0000001
x
D7

На основании структурной таблицы записываем выражения для выходных сигналов yi и функций Di :
D1 = a6 + a7 y1 = a2
D2 = a1 y2 = a2 + a3 + a5
D3 = a2 y3 = a4 + a6
D4 = a3 y4 = a4 + a7
D5 = a4
D6 = a5
D7 = a4x
Т.к. состояния автомата закодированы унитарным кодом, то можно отождествить каждое состояние с выходом соответствующего триггера, т.е. принять аi=Qi. Для принятого способа кодирования переход из одного состояния в другое как бы сопровождается сдвигом кода, за-
писанного в семиразрядном регистре. Этим и объясняется название метода. Функциональная схема автомата Мура, построенная по полученным уравнениям, приведена на рисунке 62. При определенных навыках синтез автомата Мура на базе регистра сдвига выполняется непосредственно по отмеченной ГСА без построения структурной таблицы переходов-выходов.