Лекции по теории автоматов. Прикладная теория цифровых автоматов. Методы анализа и синтеза комбинационных схем
 Скачать 3.39 Mb.
|
|
1.3. Системы (серии) логических элементов и их основные характеристики. При построении КС устройств вычислительной техники используются различные логические элементы, которые должны согласоваться по входным и выходным сигналам, напряжению питания и т.д. Для этой цели логические элементы объединяют в серии. Серией (системой, комплексом) логических элементов ЭВМ называется предназначенный для построения цифровых устройств функционально полный набор логических элементов, объединяемый общими электрическими, конструктивными и технологическими параметрами, использующий одинаковый способ представления информации, одинаковый тип межэлементных связей. Система элементов чаще всего избыточна по своему функциональному составу, что позволяет строить схемы более экономичные по количеству использованных элементов. В состав серии входят элементы для выполнения логических операций, запоминающие элементы, элементы, реализующие функции узлов ЭВМ, а также специальные элементы для усиления, восстановления и формирования сигналов стандартной формы. Конструктивно логические элементы представляют собой микроминиатюризованные интегральные электронные схемы (микросхемы), сформированные в кристалле кремния с помощью специальных технологических процессов. В большинстве современных серий элементов имеются микросхемы малой степени интеграции (ИС до 100 элементов на кристалл), средней степени (СИС – до 1000 элементов на кристалл), большой степени интеграции (БИС – до 10000 элементов на кристалл) и сверхбольшой степени интеграции (СБИС – более 10000 элементов на кристалл). Логические элементы в виде ИС реализуют совокупность простых логических операций: И, ИЛИ, И-ИЛИ, И-НЕ, ИЛИ-НЕ и т.д. Логические элементы на СИС и БИС реализуют узлы ЭВМ, на СБИС – микроЭВМ. Основными параметрами серии логических элементов являются: - питающие напряжения и сигналы для представления логического 0 и логической 1; - коэффициенты объединения по входу; - нагрузочная способность (коэффициент разветвления по выходу); - помехоустойчивость; - рассеиваемая мощность; - быстродействие. Серия элементов характеризуется количеством используемых питающих напряжений и их номинальными значениями. Обычно логическому 0 соответствует низкий уровень напряжения, а логической 1 – высокий. Для наиболее часто используемых серий напряжение питания составляет +5В, уровень логической единицы 2,4-5В, уровень логического 0 – 0-0,4В. Коэффициент объединения по входу (Коб) определяет максимально возможное число входов логического элемента, иными словами, функцию скольких переменных может реализовать этот элемент. Обычно Коб принимает значение от 2 до 4, реже Коб=8. Увеличение числа входов связано с усложнением схемы элементов и приводит к ухудшению других параметров – помехоустойчивости, быстродействия и т.д. Коэффициент разветвления по выходу (Краз) показывает на сколько логических входов может быть одновременно нагружен выход данного логического элемента. Обычно Краз для наиболее часто используемых серий равен 10. Иногда вместо Краз задается предельно допустимое значение выходного тока логического элемента в состоянии 0 или 1. Помехоустойчивость – это способность элемента правильно функционировать при наличии помех. Она определяется максимально допустимым напряжением помехи, при котором не происходит сбоя в его работе. Обычно это напряжение порядка 0,6-0,9 В. Быстродействие логических элементов является одним из важнейших параметров и характеризуется временем задержки распространения сигнала. Этот параметр существенно зависит от технологии изготовления микросхем и лежит в диапазоне от единиц до сотен наносекунд. Наиболее часто употребляемые типы интегральных микросхем – это потенциальные элементы транзисторно-транзисторной логики (ТТЛ) - серии К155, К555, К531, К1533 и т.д., транзисторной логики с эмиттерными связями (ЭСТЛ) – это серии К500,К1500, элементы на КМОП транзисторах - серии К176, К561,К564 и т.д. При синтезе КС на реальных логических элементах необходимо обязательно учитывать ограничения на Коб и Краз. 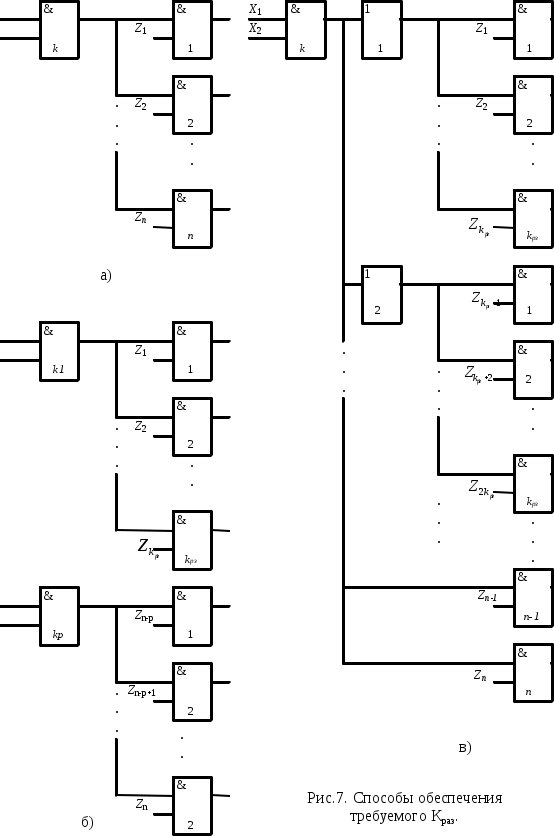 1.4. СИНТЕЗ КС С УЧЕТОМ ОГРАНИЧЕНИЙ НА  .При построении КС может оказаться, что выход k - го логического элемента нагружен  входов других ЛЭ (рис.7а). Это означает, что k - тый логический элемент перегружен и необходимо принять меры, устраняющие указанное явление. Существуют два способа обеспечения заданного :использование дополнительных развязывающих усилителей; дублирование перегруженного элемента. Схема с использованием дополнительных развязывающих усилителей представлена на рис.7.б. Количество p дополнительных усилителей, необходимых для обеспечения заданного , определяется по формуле: Недостаток рассматриваемого способа в том, что в цепь распространения сигнала вносится дополнительная задержка, что не всегда допустимо. Схема с использованием дублирования перегружаемого элемента представлена на рис.7.в. Количество p дополнительных элементов, выполняющих ту же функцию, что и К-тый элемент, определяется по формуле:  При таком способе обеспечения дополнительная задержка не вносится, но увеличивается нагрузка на элементы, формирующие сигналы  и  , что может привести к перегрузке этих элементов и введению дополнительных элементов для обеспечения заданного Краз.1.5. СИНТЕЗ КС С УЧЕТОМ ОГРАНИЧЕНИЯ НА  .Представлению функции в виде ДНФ соответствует двухуровневая КС (если считать, что на ее вход могут поступать как прямые так и инверсные входные сигналы), на первом уровне которой элементы И , а их выходы объединяются на втором уровне элементом ИЛИ . Такое построение КС обеспечивает ее максимальное быстродействие, так как ранг схемы минимален. Однако, не всегда возможно на первом уровне и, особенно, на втором выбрать логические элементы с требуемым , т.к. может оказаться, что ЛЭ с таким не выпускаются промышленностью. В этом случае необходимо с помощью нескольких элементов с меньшим получить эквивалент с большим либо, что предпочтительней, преобразовать БФ, перейдя от ДНФ к скобочной форме. Этот переход сопровождается уменьшением логических элементов, требуемого для построения схемы. Осуществить такой переход можно с помощью факторного алгоритма, суть которого рассмотрим на примере.Пусть задана некоторая булева функция в виде  Для реализации этой функции по приведенному выражению необходимо использовать 3 логических элемента 4И, один логический элемент 5И, один логический элемент 4ИЛИ. С помощью факторного алгоритма получим скобочную форму для заданной функции. Для этого обозначим все конъюнкции буквами:    и будем рассматривать их как некоторые множества. Находим попарные пересечения множеств:  ,  ,  ,  ,  ,  .Полученные пересечения показывают общие части отдельных конъюнкций. Выбираем пересечение, которое имеет наибольшую длину (если такое отсутствует, то выбирают то, которое чаще всего встречается). В данном случае это  . Поэтому из конъюнкций А и В выносим общую часть . Тогда имеем: .Обозначим F =  и находим пересечения: ,  , .Следовательно, для исходной функции имеем:  .Обозначим  ,Пересечение 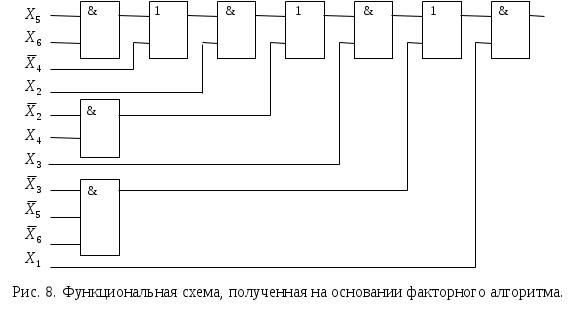 . Следовательно, окончательно имеем:   Для реализации функции по последнему выражению необходимо 5 элементов 2И, 1 элемент 3И, 3 элемента 2ИЛИ ( рис.8 ). Как видно из полученной схемы для ее реализации необходимы элементы с  = 2 или 3 (в отличие от исходной с = 4 или 5). Однако ранг схемы увеличился до 7, что приводит к увеличению задержки срабатывания схемы.1.6. Анализ комбинационных схем. Задачи анализа КС возникают при необходимости проверить правильность синтеза (на этапе проектирования) или определить БФ, реализуемую КС (при анализе или ремонте схем). Все существующие методы анализа делятся на прямые и косвенные. В результате анализа КС прямым методом получается множество наборов входных переменных, обеспечивающих заданное значение на выходе, что позволяет записать в алгебраическом виде БФ, реализуемую схемой. К прямым методам относится метод - алгоритма. Применение косвенных методов дает возможность определить реакцию схемы на заданный набор входных переменных в статике или проанализировать переходный процесс смены одного входного набора на другой. Примерами косвенных методов анализа, являются методы синхронного и асинхронного моделирования. Все упомянутые методы анализа являются машинoориентированными, что позволяет выполнить анализ схемы на ЭВМ. Для всех методов анализа необходимо описать схему в виде схемного списка, в который включается в общем случае следующие данные: номер ЛЭ в схеме; логическая функция, реализуемая ЛЭ; входные переменные для данного ЛЭ. Например, схема представленная на рис.9, может быть описана следующим списком: 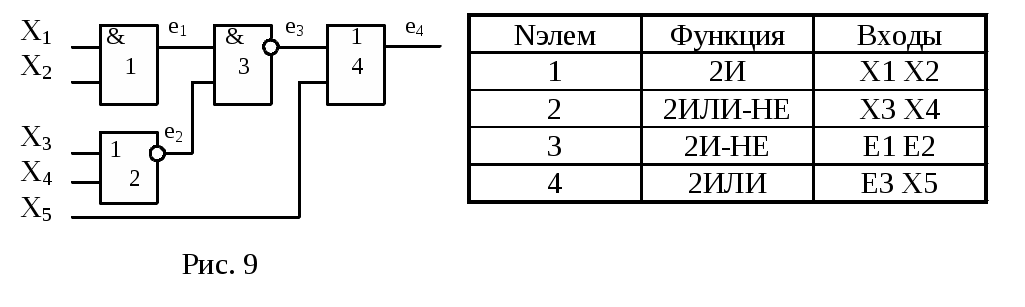 1.7. Анализ комбинационных схем методом -алгоритма. При данном методе, как упоминалось выше, ищутся наборы входных переменных, обеспечивающих заданное значение на выходе КС. Наборы, обеспечивающие на выходе КС логическую 1, образуют так называемое единичное покрытие  . Аналогично, входные наборы, обеспечивающие на выходе КС логический 0, образуют нулевое покрытие  . Рассмотрим покрытия и для простейшего логического элемента 2И, выполняющего функцию Y=X1X2. Таблица истинности для этой функции:Табл.3 Таблица истинности функции Y=X1X2 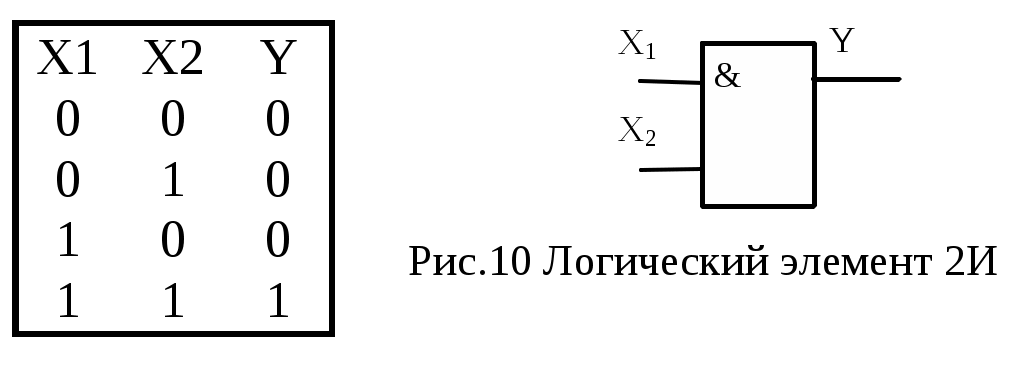 Как видно из приведенной таблицы только при единственном наборе X1=1 и X2=1 на выходе ЛЭ будет 1, т.е. единичное покрытие включает только один набор ={1 1}. На выходе ЛЭ будет 0 при трех наборах, образующих нулевое покрытие: Это покрытие можно упростить, заметив, что первый набор склеивается со вторым и третьим, т.е.  Т.о. для ЛЭ 2И можно сказать, что 1 на его выходе будет только при обеих единицах на входах, а для обеспечения 0 на выходе достаточно подать хотя бы на один вход 0. Рассуждая аналогично, получим таблицу покрытий и для основных ЛЭ, представленных ниже в табл. 4.Таблица 4. ЛЭ Y Y Y Y Y Y Y НЕ 2И 2И – НЕ 2ИЛИ 2ИЛИ–НЕ ИСК. ИЛИ 3И – НЕ X X1 X2 X1 X2 X1 X2 X1 X2 X1 X2 X1 X2 X3  1 0 X 1 1 0 0 1 X 0 0 1 1 1 X 0 X 1 1 1 0 1 1 0 X 1 X 0 0 0 1 0 X X X 0 X 1 1 0 X 0 X X X 0 При анализе схемы методом - алгоритма, задавшись определенным значением на выходе, заменяют его соответствующим покрытием элемента, формирующего выходной сигнал. В результате этого определяется, какие должны быть сигналы на выходах элементов, подключенных к выходному ЛЭ. В свою очередь, сигналы на выходах этих элементов можно заменить соответствующими покрытиями, т.е. определить значения выходных сигналов для других ЛЭ и т.д. Этот процесс продолжается до тех пор, пока не получатся покрытия, состоящие только из входных переменных, называемых опорными. Совокупность таких покрытий и дает соответствующее покрытие схемы. Пример анализа КС (рис 9. ) методом - алгоритма представлен в табл. 5. В последней колонке этой таблицы приведен оператор подстановки, в результате работы которого сигнал на выходе ЛЭ заменяется соответствующим покрытием. Необходимо обратить внимание, что все значения переменных, записанные в одной строке, должны одновременно быть в наличии для обеспечения заданного значения выходного сигнала. По- этому, при замене одного из значений в строке соответствующим покрытием, все остальные значения для других переменных в этой строке должны присутствовать совместно с этим покрытием. На основании полученного единичного покрытия можно записать БФ, реализуемую схемой:  Таблица 5 Анализ схемы методом – алгоритма.  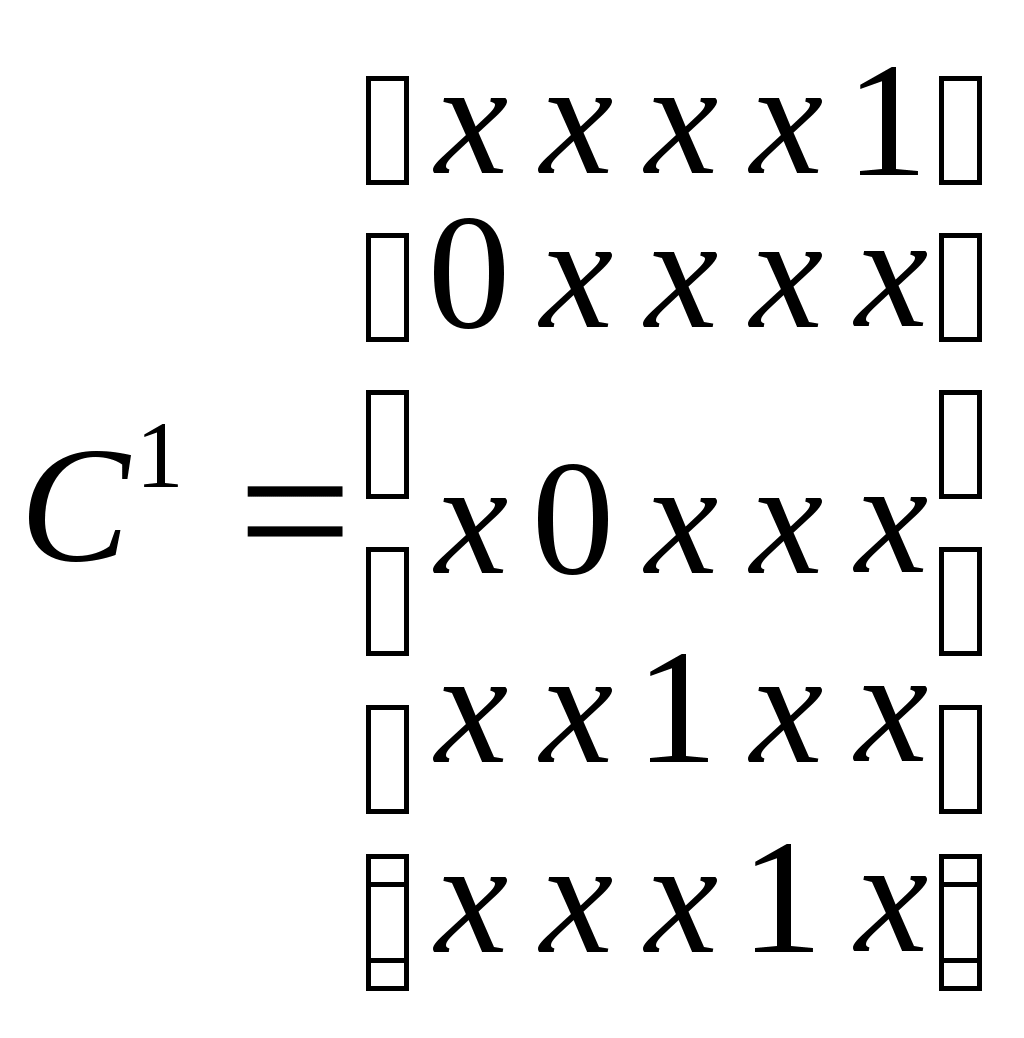 а) Получение первого покрытия  б) Получение нулевого покрытия В дальнейшем можно сравнить полученную БФ с той, по которой строилась схема и проверить правильность ее построения. При анализе схемы может оказаться, что некоторая переменная, получившая на одном из предыдущих шагов некоторые значения на данном шаге должна принять противоположное значение. Возникшее противоречие говорит о том, что данный путь является тупиковым и его необходимо исключить из дальнейшего рассмотрения. Если ни при одной комбинации входных переменных не обеспечивается значение 1(0) на выходе, то это означает, что схема реализует константу 0(1) соответственно. |