Лекции по теории автоматов. Прикладная теория цифровых автоматов. Методы анализа и синтеза комбинационных схем
 Скачать 3.39 Mb.
|
|
.
ереход автомата из одного состояния в другое осуществляется за счет изменения состояний элементов памяти. Если автомат переходит из состояния с кодом 010 в состояние с кодом 100, то это означает, что триггер V1 переходит из состояния 0 в состояние 1, V2 – из 1 в 0, V3 – сохраняет свое состояние.
ри функционировании автомата могут появиться так называемые состязания. Это явление возникает вследствие того, что элементы памяти имеют различные, хотя и достаточно близкие, времена срабатывания. Различны также задержки сигналов возбуждения, поступающих на входные каналы элементарных автоматов по логическим цепям неодинаковой длины.
, где R-количество элементов памяти. | | a1 | a2 | a3 | a4 | a5 | | | a1 | a2 | a3 | a4 | a5 |
| Z1 | a1 | a1 | a5 | a3 | a1 | | Z1 | w1 | w2 | w1 | w1 | w1 |
| Z2 | a2 | a3 | a2 | a3 | a3 | | Z2 | w1 | w3 | w4 | w2 | w2 |
| Z3 | a3 | a4 | a2 | a4 | a2 | | Z3 | w2 | w2 | w2 | w1 | w3 |
a1 N1 = 3 N3 a3 = 000
a2 N2 = 4 N2 a2 = 001
a3 N3 = 5 N1 a1 = 010
a4 N4 = 5 N4 a4 = 100
a5 N5 = 1 N5 a5 = 011
Аналогично кодированию внутренних состояний для D-триггеров можно кодировать выходные сигналы для любого типа триггеров, т.е. чем чаще вырабатывается данный выходной сигнал wi, тем меньше единиц в его коде. Так для автомата (рис.41.) имеем:
w1 N1 = 6 N1 w1 = 00
w2 N2 = 5 N2 w2 = 01
w3 N3 = 2 N3 w3 = 10
w4 N4 = 2 N4 w4 = 11
Предполагается самостоятельно окончить синтез автомата при данном кодировании и при любом другом. Результаты сравнить.
Эвристический алгоритм кодирования.
Данный алгоритм минимизирует суммарное число переключений элементов памяти на всех переходах автомата и используется для кодирования состояний автомата при синтезе на базе T, RS, JK-триггеров. Для данных типов триггеров (в отличие от D-триггеров!) на каждом переходе, где триггер меняет свое значение на противоположное, одна из функций возбуждения обязательно равна 1. Уменьшение числа переключений триггеров приводит к уменьшению количества единиц соответствующих функций возбуждения, что при отсутствии минимизации однозначно приводит к упрощению комбинационной схемы автомата.
Введем некоторые определения.
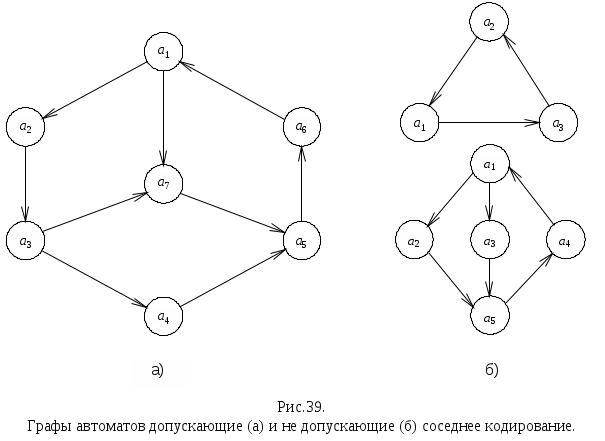
Пусть Г(S) – неориентированный граф переходов автомата S. Вершины графа отождествляются с состояниями автомата. Вершины i и j соединены ребром, если есть переход из аi и аj или наоборот.
Обозначим q(i, j) число всевозможных переходов автомата из аi в аj. Каждому ребру (i, j) графа Г(S) поставим в соответствие вес ребра р(i, j) = q(i, j) + q(j, i).
Введем функцию w(i, j) = р(i, j)d(i, j), где d(i, j) – число компонентов, которыми коды состояний аi в аj отличаются друг от друга (т.е. кодовое расстояние между кодами аi в аj).
Функция w(i ,j) имеет простой физический смысл. Перход автомата из аi в аj (или наоборот) сопровождается переключением стольких триггеров, сколькими компонентами отличаются коды этих состояний, т.е. их число равно w(i ,j). Следовательно, при переходе автомата по всем ребрам, соединяющим состояниям аi и аj (их число p(i, j)!) всего переключится количество триггеров, равное p(i, j)d(i ,j) =w(i ,j).
Но тогда функция
показывает, сколько всего переключается триггеров при прохождении автомата по всем возможным переходам. Функция w показывает, сколько всего единиц в функции возбуждения, т.е. позволяет оценивать сложность комбинационной схемы автомата. Wможно рассматривать как некую целевую функцию, минимум которой определит такое кодирование, при котором комбинационная схема наиболее простая. Кстати, миинмальное кодовое расстояние между различными состояниями равно 1 и если удается закодировать все состояния соседним кодированием, то очевидно, что w будет минимально возможным и равным 
, т.е. суммарному числу переходов для автомата.Из выражения для w следует, что переход из аi в аi, для которого d(i,i)=0, не влияет на w (что вполне очевидно, если учесть, что на этом переходе ни один триггер не переключается).
Рассмотрим применение эвристического алгоритма на конкретном примере автомата, заданного таблицами переходов и выходов (рис.41. ). Для данного автомата можно построить ориентированный граф (без учета петель), представленный на рис.42. На каждом ребре указан его вес.
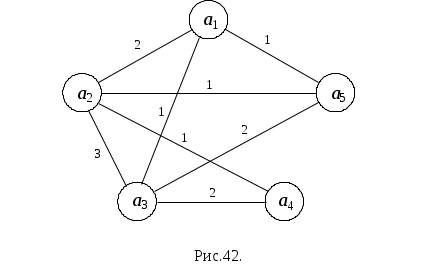
Эвристический алгоритм состоит из следующих шагов.
1. Строим матрицу
, состоящую из всех пар номеров (i, j), для которых р(i, j) 0 (т.е. в автомате есть переход из аi в аj или наоборот) и i<j. Для каждой пары в матрице указываем ее вес р(i, j), совпадающий с весом ребра соединяющего аi и аj.-
i
j
p(i,j)
1
2
2
1
3
1
T
=
1
5
1
2
3
3
2
4
1
2
5
1
3
4
2
3
5
2
2. Упорядочим строки матрицы
, для чего построим матрицу 
следующим образом. В первую строку матрицы поместим пару (,) с наибольшим весом р(,). В нашем случае (,) = (2,3), р(2,3) = 3. Из всех пар, имеющих общий компонент с парой (,) выбирается пара (,) с наибольшим весом и заносится во вторую строку матрицы . Ясно, что {,}{,}0. Затем из всех пар, имеющих общий компонент хотя бы с одной из внесенных уже в матрицу пар выбирается пара с наибольшим весом и заносится в матрицу и т.д.. В случае равенства весов пар вычисляются суммы весов компонентов пар (весом р() компонента называется число появлений в матрице ) и в матрицу заносится пара с наибольшей суммой весов. В рассматриваемом автомате на второе место вслед за парой (2,3) претендуют пары: (1,2) с р(1,2) = 2; (3,4) с р(3,4) = 2, (3,5) с р(3,5) = 2.Для определения того, какая пара займет второе место в матрице
находим веса компонентов пар:р(1) = 3 р(2) = 3 р(1) + р(2) = 6
р(3) = 4 р(4) = 2 р(3) + р(4) = 6
р(3) = 4 р(5) = 2 р(3) + р(5) = 6
В данном случае для всех пар совпадают и их веса и веса их компонентов. Поэтому на второе место матрицы
может быть поставлена любая из пар (1,2), (3,4), (3,5). Но тогда на 3-м и 4-м будут остальные две. Выполнив упорядочивание всех пар, получим матрицу в виде: -
i
j
p(i,j)
2
3
3
1
2
2
M
=
3
4
2
3
5
2
1
3
1
1
5
1
2
4
1
2
5
1
3. Определяем разрядность кода для кодирования состояний автомата (количество элементов памяти – триггеров). Всего состояний M=5. Тогда
R = ]log2M[ = ]log25[ =3.
Закодируем состояния из первой строки матрицы следующим образом: K2 = K(а2) = 000; K3 = K(а3) = 001.
Для удобства кодирования будем иллюстрировать этот процесс картой Карно:
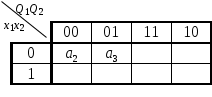
Вычеркнем из матрицы
первую строку, соответствующую закодированным состояниям а2 и а3. Получим матрицу .-
i
j
p(i,j)
1
2
2
3
4
2
M’
=
3
5
2
1
3
1
1
5
1
2
4
1
2
5
1
5. В силу упорядочивания п.2 в первой строке закодирован ровно один элемент. Выберем из первой строки незакодированный элемент и обозначим его . (В нашем случае = 1).
6. Строим матрицу
, выбрав из 
строчки, содержащие .-
i
j
p(i,j)
1
2
2
M
=
M’
=
1
3
1
1
5
1
Пусть B = {1,...,F} – множество элементов из матрицы
, которые уже закодированы. Их коды К1,..., KFсоответственно. В нашем случае:B = B3 = {2,3} K2 = 000 K3 = 001.
7. Для каждого Kf (f=1, ..., F) найдем
– множество кодов, соседних с 
и еще не занятых для кодирования состояний автомата. (Для соседних кодов кодовое расстояние d=1).K2 = 000
= {100, 010}K3 = 001
= {011, 101}.Построим множество
Если оказывается, что
, то строим новое множество 
, где 
– множество кодов, у которых кодовое расстояние до кода равно 2 и т.д..8. Для каждого кода из множества D находим кодовое расстояние до кода
.K2 = 000 K3 = 001
d(100, 000) = 1 d(100, 001) = 2
d(010, 000) = 1 d(010, 001) = 2
d(011, 000) = 2 d(011, 001) = 1
d(101, 000) = 2 d(100, 001) = 1
9. Находим значение функции w для каждого кода из множества D.
10. Из множества D выбираем код K, у которого получилось минимальное значение w в п.9. Выбираем код для состояния a1 К1 =100.
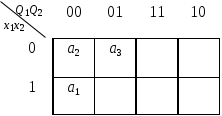
11. Из матрицы
вычеркиваем строки, в которых оба элемента уже закодированы, в результате чего получим новую матрицу . Если в новой матрице не осталось ни одной строки, то кодирование закончено. В противном случае возвращаемся к п.5. В нашем случае имеем:-
i
j
p(i,j)
3
4
2
3
5
2
M’
=
1
5
1
2
4
1
2
5
1
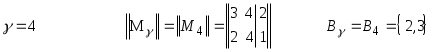
К2 = 000
= {010}K3 = 001
= {011, 101}
K2 = 000 K3 = 001
d(010, 000) = 1 d(010, 001) = 2
d(011, 000) = 2 d(011, 001) = 1
d(101, 000) = 2 d(101, 001) = 1
Выбираем К4 = 101.
К1 = 100
= {110}K2 = 000
= {010}К3 = 001
= {011}
К1 = 100 K2 = 000 K3 = 001
d(110, 100) = 1 d(110, 000) = 2 d(110, 001) = 3
d(010, 100) = 2 d(010, 000) = 1 d(010, 001) = 2
d(011, 100) = 3 d(011, 000) = 2 d(011, 001) = 1
Выбираем К5 = 011.
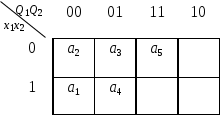
Т.к. все состояния автомата закодированы, то работа алгоритма заканчивается. Общее количество переключений триггеров:
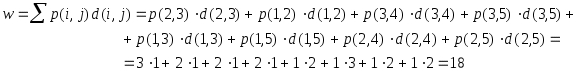
Минимально возможное количество переключений (если бы состояния были закодированы соседним кодированием)
Коэффициент эффективности кодирования:
Рассмотренный алгоритм кодирования является машино-ориентированным, существуют программы, реализующие этот алгоритм.
Необходимо отметить в заключении, что использование алгоритма кодирования для D-триггеров или эвристического алгоритма для других типов триггеров обеспечивает наиболее простую с точки зрения реализации схему, но при этом возможны гонки. Для радикального устранения последних используют аппаратные методы – триггеры с двойной памятью: триггеры, управляемые фронтом и т.д..
Управляющие и операторные автоматы.
Принцип микропрограммного управления.
ЭВМ перерабатывает информацию, выполняя над ней какие-то операции. Для выполнения операций над информацией используются операционные устройства – процессоры, каналы ввода-вывода, устройства управления внешними устройствами и т.д. Функцией операционного устройства является выполнение заданного множества операций F={f1,...,fG} над входными словами D={d1,...,dH} c целью вычисления слов R={r1,...,rQ}, которые представляют результаты операций R=fg(D), где g=1,2,...,G.
Функциональная и структурная организация операционных устройств базируется на принципе микропрограммного управления, который состоит в следующем:
1. Любая операция fg(g=1,...,G), реализуемая устройством, рассматривается как сложное действие, которое разделяется на последовательность элементарных действий над словами информации. Эти элементарные действия называются микрооперациями.
2. Для управления порядком следования микроопераций используются логические условия, которые в зависимости от значений слов, преобразуемых микрооперациями, принимают значения "ложь" или "истина" (1 или 0).
3. Процесс выполнения операций в устройстве описывается в форме алгоритма, который представляется в терминах микроопераций и логических условий и называется микропрограммой. Микропрограмма определяет порядок проверки значений логических условий и следования микроопераций, необходимый для получения требуемых результатов.
4. Микропрограмма используется как форма представления функции устройства, на основе которой определяется структура и порядок функционирования устройства во времени.
Т.о. из принципа микропрограммного управления следует, что структура и порядок функционирования операционных устройств предопределяется алгоритмом выполнения операции F={f1,...,fG}.
К элементарным действиям над словами информации микрооперациям относятся: передача информации из одного регистра в другой, взятие обратного кода, сдвиг и т.д.
Понятие операционного и управляющих автоматов.
Как показал академик В.М. Глушков в любом устройстве обработки цифровой информации можно выделить два основных блока – операционный автомат (ОА) и управляющий автомат (УА).
Операционный автомат (ОА) служит для хранения слов информации, выполнения набора микроопераций и вычисления значений логических условий, т.е. операционный автомат является структурой, организованной для выполнения действий над информацией. Микрооперации, выполняемые ОА, задаются множеством управляющих сигналов Y={y1,....,yM}, с каждым из которых отождествляется определенная микрооперация.
Значения логических условий, вычисляемые в операционном автомате, отображаются множеством осведомительных сигналов X={x1,...,xL}, каждый из которых отождествляется с определенным логическим условием.
Управляющий автомат (УА) генерирует последовательность управляющих сигналов, предписанную микропрограммой и соответствующую значениям логическим условий. Иначе говоря, управляющий автомат задает порядок выполнения действий в ОА, вытекающий из алгоритма выполнения операций. Наименование операции, которую необходимо выполнить в устройстве, определяется кодом g операции, поступающим в УА извне. По отношению к УА сигналы g1,...,gh, посредством которых кодируется наименование операции и осведомительные сигналы x1,...,xL, формируемые в операционном автомате, играют одинаковую роль: они влияют на порядок выработки управляющих сигналов Y. Поэтому сигналы g1,...,gh и x1,...,xL относятся к одному классу – к классу осведомительных сигналов, поступающих на вход УА.
Т.о. любое операционное устройство – процессор, канал ввода-вывода и т.д. – является композицией операционного и управляющего автоматов. Операционный автомат, реализуя действия над словами информации, является исполнительной частью устройства, работой которого управляет управляющий автомат, генерирующий необходимые последовательности управляющих сигналов.
Операционный и управляющий автоматы могут быть определены своими функциями – перечнем выполняемых ими действий.
Функция ОА определяется следующей совокупностью сведений:
1) множеством входных слов D={d1,...,dH}, вводимых в автомат в качестве операндов;
2) множеством выходных слов R={r1,...,rQ}, представляющих результаты операций;
3) множеством внутренних слов S={s1,...,sN}, используемых для представления информации в процессе выполнения операций. Можно считать, что входные и выходные слова совпадают с определенными внутренними DS, RS.
4) множеством микроопераций Y={ym}, реализующих преобразование S=m(s) над словами информации, где m – вычисляемая функция;
5) множеством логических условий X={xi}, где xi=i(si) и i – булева функция;
T.o. функция ОА задана, если заданы (определены) множества D, R, S, Y, X. Время не является аргументом функции ОА. Функция устанавливает список действий-микроопераций и логических условий, которые может выполнять автомат, но никак не определяет порядок следования этих действий во времени. Т.е. функция ОА характеризует средства, которые могут быть использованы для вычислений, но не сам вычислительный процесс.
Порядок выполнения действий во времени определяется в форме функций управляющего автомата.
Функция управляющего автомата – это операторная схема алгоритма ( микропрограммы), функциональными операторами которой являются символы у1,...,уm, отождествляемые с микрооперациями, и в качестве логических условий используются булевы переменные х1,...,хL. Операторная схема алгоритма наиболее часто представляется в виде граф-схемы алгоритма (ГСА). ГСА определяет вычислительный процесс последовательно во времени, устанавливая порядок проверки логических условий х1-хL и порядок следования микроопераций у1-уm.
СПОСОБЫ ОПИСАНИЯ АЛГОРИТМОВ И МИКРОПРОГРАММ
Наиболее наглядно изображать микропрограммы и алгоритмы в виде ориентированного графа, т.н. граф схемы алгоритма (ГСА). Кроме наглядности это дает возможность использовать для анализа и преобразования микропрограмм эффективные методы теории графов. При графическом описании отдельные функции алгоритмов (микрооперации) отображаются в виде условных графических изображений, т.н. вершин. В ГСА обычно используют вершины следующих типов:
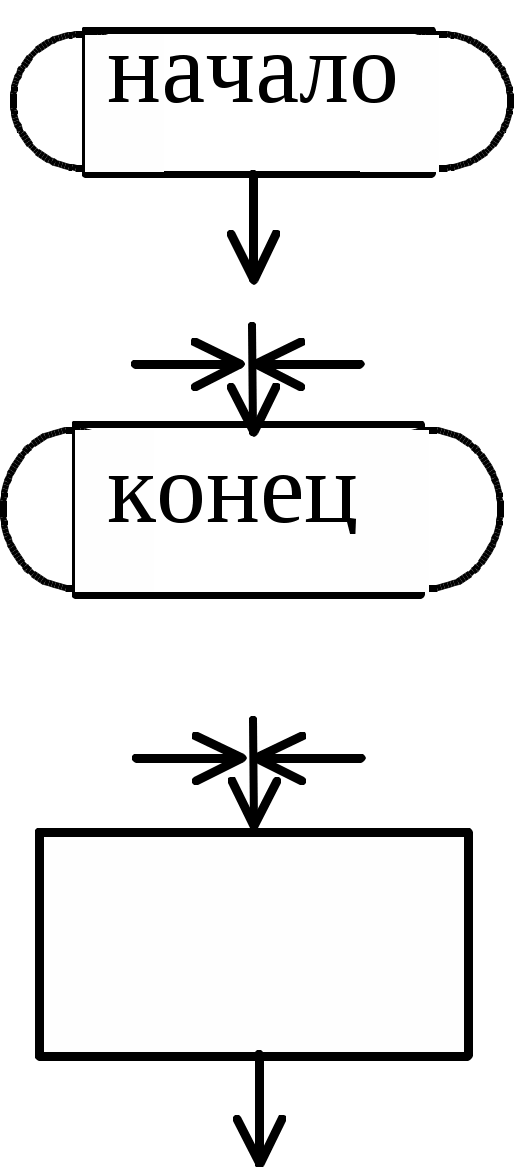
- вершина «начало» имеет один выход, входов не имеет. Обозначает начало микропрограммы.
- вершина «конец» имеет любое число входов, выходов не имеет. Обозначает конец микропрограммы.
- операторная вершина имеет любое число входов, один выход. Внутри операторной вершины записывается одна микрокоманда - совокупность микроопераций, допускающих совместное (т.е. одновременное) выполнение.
- условная вершина имеет любое число входов и 2 выхода. Внутри условной вершины записывается булевое выражение, в зависимости от значения которого осуществляется выбор направления дальнейшего выполнения микропрограммы.
- особый вид условной вершины - ждущая - имеет множество входов, 2 выхода, 1 из которых заведен на вход. При попадании в ждущую вершину выход из нее возможен только при выполнении условия Х.
Граф микропрограммы состоит из совокупности перечисленных вершин и дуг, соединяющих выходы одних вершин с входами других. Соединение вершин и направление дуг графа определяют исходя из алгоритма операции, описываемого графом, и структуры операционного автомата.
Сама микропрограмма и ее граф должны быть корректны, т.е. отвечать следующим условиям:
1. В графе должна быть только одна начальная и одна конечная вершина.
2. В любую вершину графа должен вести по крайней мере один путь из начальной вершины.
3. Из каждого выхода любой вершины графа должен существовать по
крайней мере один путь в конечную вершину.
4. При всех возможных значениях логических условий и используемых слов должен существовать путь из начальной вершины в конечную.
Пример ГСА представлен на рисунке:
ГСА на рис.43 называется содержательной, т.к. внутри вершин записаны в явном виде микрооперации и логические условия. Если же каждую микрооперацию обозначить символами Yi, a логические условия через Xi, то получится так называемая кодированная ГСА (рис.44 ). Для правильного восприятия микропрограммы, заданной в виде кодированной ГСА, необходимо знать соответствия между Yi, Xi и содержанием соответствующих микроопераций и логических условий.
Для записи микроопераций внутри вершин используется так называемый Ф-язык. Подробно с зтим языком можно ознакомиться в последующих курсах «Схемотехника ЭВМ», «Теория и проектирование ЭВМ». Здесь же мы рассмотрим только основные положения этого языка.
В этом языке существуют двоичные константы и переменные: 0010 - константа, A(1:4) - четырехразрядное слово - четырехразрядная двоичная переменная. Например, A(1:4)=1010 означает, что в первом разряде слова A будет 1, во втором - 0 и т.д. A(2:3) - часть слова A, размещенная во втором и третьем разрядах.
Наиболее употребительные операции Ф-языка:
присваивание - A( 0:3 ): = 1000, B( 1:4 ): = A( 5:8 ) и т.д.
инвертирование - A( 0:3 ): = ^ B( 1:4 )
конкатенации - С( 0:6 ): = A( 0:3 ). B( 1:3 )
Пример 1. A( 0:3 ): = 1100 B( 1:4 ): = A( 0:3 ) B( 1:4 ): = 1100
2. B( 1:4 ): = 0101 A( 0:3 ): = ^B( 1:4 ) A( 0:3 ): = 1010
3. A( 0:3 ): = 1101 B( 1:3 ): = 110 C( 0:6 ): = A( 0:3 ). B( 1:3 ) C(0:6):=1101110
Запись вида A(2) означает, что здесь рассматривается второй разряд слова A, т.е. это бит, записанный во втором разряде слова A.
При выполнении операций присваивания необходимо соблюдать равенство разрядов в словах слева и справа от знака присваивания. Операции сложения, логического сложения и т.д. в Ф-языке записываются обычным способом через оператор присваивания:
C(0:n):=A(0:n)+B(0:n)
D(0:n):=A(0:n)vB(0:n) и т.д.