Лекции по теории автоматов. Прикладная теория цифровых автоматов. Методы анализа и синтеза комбинационных схем

• Название: Прикладная теория цифровых автоматов. Методы анализа и синтеза комбинационных схем
• Дата: 10.01.2023
• Размер: 3.39 Mb.
• Имя файла: Лекции по теории автоматов.doc
• Тип: Документы; #880461
• страница: 3 из 10

1. 8 Анализ КС методом синхронного моделирования.
При данном методе считается, что все ЛЭ переключаются одновременно, без задержки. В результате применения метода определяется установившееся значение сигнала на выходе схемы.

Рассмотрим метод синхронного моделирования на примере схемы ( рис.9 ).

На первом этапе схему разбиваем на уровни и записываем в порядке возрастания уровня уравнения, описывающие функционирование ЛЭ:

№уровня	№элемента	уравнение
1	1 2	e1 = X1 X2 e2 =
2	3	e3 =
3	4	Y = e4 = e3 + X5

Проанализируем схему при подаче на вход набора X₁=0, Х₂=0, Х₃=0, Х₄=1, Х₅=1. Для этого решаем записанные уравнения в порядке возрастания уравнения. Имеем:
;

;

;

.

Следовательно, при подаче на вход набора {00011}, на выходе будет Y=1. Аналогично можно промоделировать работу схемы при подаче на вход любого другого набора.

1.9 Анализ КС методом асинхронного моделирования.
Реальный ЛЭ переключается за какое-то конечное время, зависящее от технологии изготовления, условий эксплуатации, емкостей нагрузки и т.д. Прохождение сигнала последовательно через несколько ЛЭ будет приводить к накоплению времени задержки и возникновению сдвига во времени выходного сигнала по отношению ко входному. Наличие задержки и порождаемого ею временного сдвига сигналов может приводить к появлению на выходе отдельных ЛЭ и всей схемы в целом кратковременных сигналов, не предусмотренных БФ, реализуемой схемой. Как иллюстрацию, рассмотрим схему рис.11, а .





Рис. 11 а)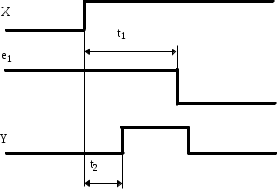





Рис. 11 . Статический риск сбоя.

а)- схема, б)- временные диаграммы.

t₁-время задержки инвертора

t₂-время задержки элемента 2И
Данная схема реализует функцию , т.е. константу 0 независимо от входного сигнала X. Однако в переходном процессе в результате задержки срабатывания ЛЭ возможна ситуация, когда на обоих входах элемента 2И будут логические единицы, что может привести к появлению на выходе схемы логической 1 (см. рис.11 б). Рассмотренный случай возможен при задержке срабатывания второго элемента больше, чем первого. Такое явление называется риском сбоя. Различают статистический и динамический риски сбоя.

При статическом риске сбоя до и после переходного процесса состояние выходного сигнала одно и то же, а во время переходного процесса возможно кратковременное появление противоположного сигнала.

При динамическом риске сбоя до и после переходного процесса состояния выходного сигнала противоположные, но в переходном процессе выходной сигнал несколько раз меняет свое значение. Динамический риск сбоя возможен в схеме (рис.12 а) при смене набора (Х₁=0, Х₂=1, Х₃=1) на набор (Х₁=1, Х₂=0, Х₃=0) и иллюстрируется диаграммами (рис.12 б).

В данном примере динамический риск сбоя на выходе КС сопровождается статическим на выходе элемента 1. Как видно из временных диаграмм риск сбоя имеет место при наличии определенного временного сдвига между сигналами, поступающими на вход ЛЭ. Нежелательные сигналы на выходе могут и отсутствовать при другом соотношении временных сигналов, однако принципиальная возможность их появления является фактором снижающим надежность работы схемы. Поэтому очень важно уметь обнаруживать и устранять такие явления.



Для анализа процесса переключения КС при смене входных наборов и обнаружения рисков сбоя используется метод асинхронного моделирования. При этом методе считается, что каждый элемент переключается с одинаковой задержкой. Анализ включает такие этапы:

1.Каждому элементу схемы присваивается уровень, причем уровень 1 имеют элементы, все входы которых являются независимыми входами схемы.

2.Записываются уравнения, описывающие каждый ЛЭ в порядке убывания уровня.

3.Для исходного входного набора А(X₁, X₂, … , X_n ) определяется значение сигналов на выходах всех ЛЭ схемы. Пусть данный набор А заменяется набором В(X₁, X₂, … , X_n ).

4.Помечаются те уравнения, в правой части которых хотя бы одна из переменных изменила свое значение.

5.Решаются помеченные уравнения в порядке их записи в схеме . После решения уравнение считается непомеченным.

6.Если после решения всех уравнений системы переменные, входящие в левые части уравнений, изменили свои значения, то вновь помечаются те уравнения, в правые части которых входят эти переменные. Затем осуществляется переход к п.5. В противном случае моделирование данного входного набора считается законченным. Выполнение п.5 называется тактом моделирования.

Анализ схемы (рис.13) методом асинхронного моделирования приведен ниже. Для данной схемы входной набор А(1011110) заменяется набором В(1101011).





Рис. 13. Комбинационная схема для метода асинхронного моделирования.
Уравнения, описывающие ЛЭ:

	1-ый такт	2-ой такт	3-ий такт
Y= e6 = e4 + e5 + X5 e5 = e3 X7 e3=X5 X6 e2=X5 X4 e1=X1 X2	* * - * * *	* * * - - -	* - - - - -

Табл. 6 Таблица моделирования схемы

Выходы Такты моделирования Прим.

0 1 2 3
e₆ 1 0 1 0 дин.
e₅ 0 1 0 0 стат.
e₄ 0 0 0 0
e₃ 1 0 0 0
e₂ 1 0 0 0




e₁ 0 1 0 1

Как следует из результатов моделирования, при смене набора А набором В на выходе элемента 4 имеет место статический риск сбоя, а на выходе схемы - динамический риск сбоя.

Радикальным способом устранения рисков сбоя является введение стробирования для снятия выходного сигнала КС. Стробирующий импульс подается после окончания переходного процесса в КС (т.е. когда на выходе КС уже установилось необходимое значение выходного сигнала), что исключает влияние возможных сбоев на вырабатываемый схемой сигнал.

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ АБСТРАKТНЫХ АВТО­МАТОВ.

Ознакомившись в курсах "Программирование" и "Машинная арифметика" с принципами работы ЭЦВМ, можно ука­зать на две основные особенности таких вычислительных машин: оперирование данными, представленными в цифровой форме и автоматическая работа по заранее составленной программе. Эти особенности показывают, что любая ЭЦВМ является цифровым автоматом (ЦА). Понятие ЦА служит обобщением для всех видов устройств обработки цифровой информации, имеющих программное управление.

Цифровой автомат - устройство, характеризующееся набором внутренних состояний в которое оно попадет под воз­действием команд заложенной в него программы. Переход автомата из одного состояния в другое осуществляется в определенный момент времени.

Математической моделью ЦА (а в общем случае любого дискретного устройства) является так называемый абстракт­ный автомат, определенный как 6-компонентный кортеж: S=(A,Z,W,,,а₁) у которого:

1. A={a₁, a₂, ... ,a_m} - множество состояний (внутренний алфавит)

2. Z={z₁, z₂, ... ,z_f} - множество входных сигналов (входной алфавит)

3. W={w₁, w₂, ..., w_g} - множество выходных сигналов (выходной алфавит)

4.  : AZA - функция переходов, реализующая отображение D_ АZ в А. Иными словами функция  некоторым парам состояние - входной сигнал (а_m, z_f) ставит в соответствие состояния автомата а_s=  (a_m, z_f), a_sA.

5.  : AZW - функция выходов, реализующая отображение D_ АZ на W. Функция  некоторым парам состояние - входной сигнал (а_m, z_f) ставит в соответствие выходные сигналы автомата Wg=(а_m, z_f) , WgW.

6. a_i A - начальное состояние автомата.

Под алфавитом здесь понимается непустое множество попарно различных символов. Элементы алфавита называются буквами, а конечная упорядоченная последовательность букв - словом в данном алфавите.





Абстрактный автомат (рис.14) имеет один вход и один выход. Автомат работает в дискретном времени, принимающем целые неотрицательные значения t = 0,1,2,... В каждый момент t дискретного времени автомат находится в некотором состоянии a(t) из множества состояний автомата, причем в начальный момент t = 0 он всегда находится в начальном со­стоянии a(0)=a1. В момент t, будучи в состоянии a(t), автомат способен воспринять на входе букву входного алфавита z(t)  Z. В соответствии с функцией выходов он выдаст в тот же момент времени t букву выходного алфавита W(t)=(a(t), z(t)) и в соответствии с функцией переходов перейдет в следующее состояние a(t+1)=[a(t), z(t)], a(t) A, w(t) W.

Смысл понятия абстрактного автомата состоит в том, что он реализует некоторое отображение множества слов вход­ного алфавита Z во множество слов выходного алфавита W. Т.е. если на вход автомата, установленного в начальное состояние a1, подавать буква за буквой некоторую последовательность букв входного алфавита z(0), z(1),... - входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита w(0), w(1),... - выходное слово. Т.о. выходное слово = (входное слово), где  - отображение, осуществляемое абстрактным автоматом.

На уровне абстрактной теории понятие "работа автомата" понимается как преобразование входных слов в выходные. Можно сказать, что в абстрактном автомате отвлекаемся от его структуры - содержимого прямоугольника (рис. 14 ), рассматривая его как "черный ящик", т.е. основное внимание уделяем поведению автомата относительно внешней среды.

Понятие состояния в определении автомата введено в связи с тем, что часто возникает необходимость в описании пове­дения систем, выходы которых зависят не только от состояния входов в данный момент времени, но и от некоторой пре­дыстории, т.е. от сигналов, которые поступали на входы системы ранее. Состояния как раз и соответствуют некоторой памяти о прошлом, позволяя устранить время как явную переменную и выразить выходной сигнал как функцию со­стояния и входа в данный момент времени.

На практике наибольшее распространение получили два класса автоматов - автоматы Мили (Mealy) и Мура (Moore).

Закон функционирования автомата Мили задается уравнениями:

a(t+1) = (a(t), z(t)); w(t) = (a(t), z(t)), t = 0,1,2,...

Закон функционирования автомата Мура задается уравнениями:

a(t+1)=(a(t), z(t)); w(t) = (a(t)), t = 0,1,2,...

Из сравнения законов функционирования видно, что, в отличие от автомата Мили, выходной сигнал в автомате Мура зависит только от текущего состояния автомата и в явном виде не зависит от входного сигнала. Для полного задания автомата Мили или Мура дополнительно к законам функционирования, необходимо указать начальное состояние и оп­ределить внутренний, входной и выходной алфавиты.

Кроме автоматов Мили и Мура иногда оказывается удобным пользоваться совмещенной моделью автомата, так на­зываемым С- автоматом.

Под абстрактным С- автоматом будем понимать математическую модель дискретного устройства, определяемую восьми­компонентным вектором S=( A, Z, W, U, , ₁, ₂, а₁ ), у которого:

1. A={a₁, a₂, ... ,a_m} - множество состояний;

2. Z={z₁, z₂, ... ,z_f} - входной алфавит;

3. W={w₁, w₂, ..., w_g} - выходной алфавит типа 1;

4. U={u₁, u₂,...,u_h} - выходной алфавит типа 2;

5.  : A  Z  A - функция переходов, реализующая отображение D_ АZ в А;

6. ₁ : A  Z  W - функция выходов, реализующая отображение D_1 АZ в W;

7. ₂ : A  U - функция выходов, реализующая отображение D_2  А в U;

8. а₁  А - начальное состояние автомата.

Абстрактный С- автомат можно представить в виде устройства с одним входом, на который поступают сигналы из входного алфавита Z, и двумя выходами, на которых появляются сигналы из алфавитов W и U. Отличие С - автомата от моделей Мили и Мура состоит в том, что он одновременно реализует две функции выходов ₁ и ₂, каждая из которых характерна для этих моделей в отдельности. Закон функционирования С- автомата можно описать следующими уравнениями:

а( t + 1) = ( a( t ), z( t )); w( t ) = ₁( a ( t ), z( t )); u( t ) = ₂( a( t )); t = 0, 1, 2, ...
Выходной сигнал U_h=₂( a_m ) выдается все время, пока автомат находится в состоянии a_m. Выходной сигнал Wg=₁( a_m, z_f ) выдается во время действия входного сигнала Z_f при нахождении автомата в состоянии a_m.

Рассмотренные выше абстрактные автоматы можно разделить на:

1. 
   полностью определенные и частичные;
   
2. 
   детерминированные и вероятностные;
   
3. 
   синхронные и асинхронные;
   

Полностью определенным называется абстрактный цифровой автомат, у которого функция переходов и функция выходов определены для всех пар ( a_i, z_j ).

Частичным называется абстрактный автомат, у которого функция переходов или функция выходов, или обе эти функ­ции определены не для всех пар ( a_i, z_j ).

К детерминированным относятся автоматы, у которых выполнено условие однозначности переходов : автомат, находя­щийся в некотором состоянии a_i, под действием любого входного сигнала z_j не может перейти более, чем в одно состоя­ние.

В противном случае это будет вероятностный автомат, в котором при заданном состоянии a_i и заданном входном сиг­нале z_j возможен переход с заданной вероятностью в различные состояния.

Для определения синхронных и асинхронных автоматов вводится понятие устойчивого состояния. Состояние a_s автомата называется устойчивым, если для любого состояния a_i и входного сигнала z_j таких, что ( a_i, z_j ) = a_s имеет место ( a_s, z_j ) = a_s, т.е. состояние устойчиво, если попав в это состояние под действием некоторого сиг­нала zj, автомат выйдет из него только под действием другого сигнала z_k, отличного от z_j.

Автомат, у которого все состояния устойчивы - асинхронный.

Автомат называется синхронным, если он не является асинхронным.

Абстрактный автомат называется конечным, если конечны множества А = {a₁, a₂, ..., a_m}, Z = {z₁, z₂, ..., z_f}, W = {w₁, w₂, ..., w_g}. Автомат носит название инициального, если в нем выделено начальное состояние a₁.