Лекции по теории автоматов. Прикладная теория цифровых автоматов. Методы анализа и синтеза комбинационных схем
 Скачать 3.39 Mb.
|
ОПЕРАЦИОННЫЕ ЭЛЕМЕНТЫСогласно принципа микропрограммного управления, любая сложная операция распадается на ряд микроопераций, которые выполняются ОА. Различные микрооперации выполняются элементарными ОА - так называемыми операционными элементами (ОЭ), которые являются составными частями основного ОА. Под операционным элементом понимают устройство, реализующее одну из следующих функций или их произвольную комбинацию: хранение слова информации С; выполнение некоторых микроопераций, в результате которых вычисляется новое значение слова С; вычисления логического условия, зависящего от слова С; Т.о. функция ОЭ определена, если заданы: описание хранимого или вычисляемого слова; описание множества микроопераций, выполняемых этим элементом; описание вычисляемых этим элементом логических условий. Для построения ОА ОЭ соединяются между собой с помощью цепей передачи слов информации от выходов одних элементов к входам других. В зависимости от выполняемых микроопераций ОЭ делятся на разновидности: шина, регистр, счетчик, сумматор, схема сравнения, дешифратор, шифратор и т.д. Шина - это совокупность цепей, предназначенных для передачи слова информации. Условное обозначение шины представлено на рис.45. 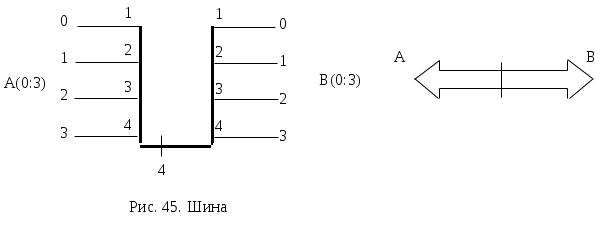 Шины, изображенные на рис.45 называются неуправляемыми шинами. Управляемые шины представлены на рис.46. 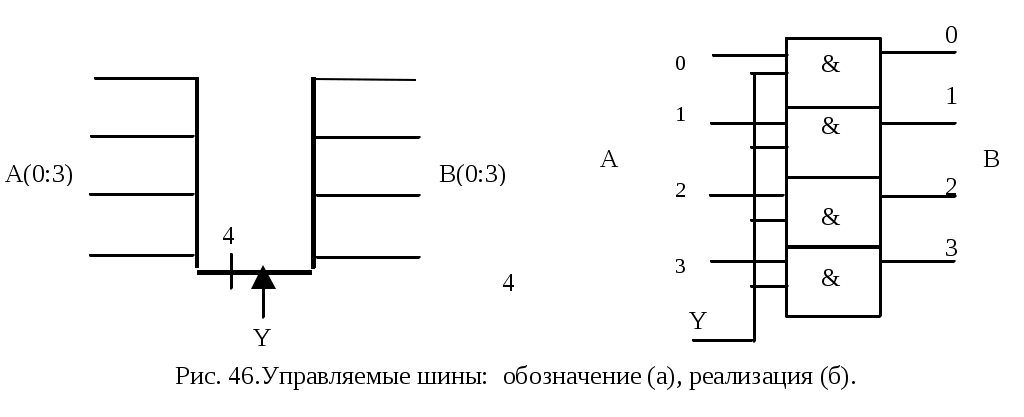 Под действием управляющего сигнала у управляемая шина выполняет микрооперации: у=0 : B(0:3):=0 , y=1 : B(0:3):=A(0:3) Т.е. при y=1 осуществляется операция передачи. Разрядность шины может быть произвольная, но обычно это 8, 12, 16, 24, 32 и т.д. Регистр - это операционный элемент, служащий для запоминания слов и обеспечивающий в общем случае выполнение следующих микроопераций: установка регистра в 0 (сброс); прием слова из другого регистра, шины и т.д.; передача слова на другой регистр, шину и т.д.; преобразование кодов хранимых слов в инверсные коды; сдвиг хранимого слова влево или вправо на требуемое число разрядов.  Регистр, выполняющий такие микрооперации, называется многофункциональным. Т.к. регистр предназначен для хранения информации, то он содержит элементы памяти, в качестве которых используются триггеры. Количество триггеров определяет разрядность регистра. Будем обозначать регистр в виде прямоугольника с указанием разрядности (рис.47 ). Регистр может состоять из отдельных подрегистров, имеющих самостоятельное значение (рис.48.). На рис.48 представлен регистр, хранящий число в форме с плавающей запятой. В этом регистре три подрегистра: для хранения знака Рг(0), характеристики Рг(1:7), мантиссы Рг(8:31) числа. Регистр может выполнять ряд микроопераций, например: 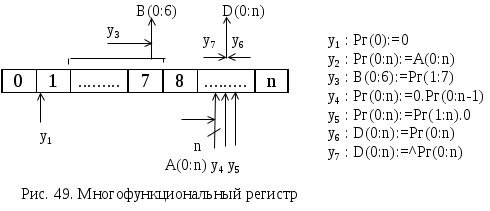 Регистр, который выполняет микрооперацию у4 (сдвиг вправо) или у5 (сдвиг влево) называются регистром сдвига. Сумматор - операционный элемент, выполняющий суммирование кодов чисел. В зависимости от кодов чисел различают сумматоры прямого, обратного, дополнительного кодов. Кроме того, сумматоры бывают комбинационными и накапливающими. Комбинационный сумматор вырабатывает выходные сигналы суммы и переноса, определяемые комбинацией цифр слагаемых, одновременно поданных на входы сумматора. Данный сумматор не обладает памятью и после снятия сигналов с входов выходные сигналы также исчезают. Условное обозначение комбинационного сумматора представлено на рис.50. 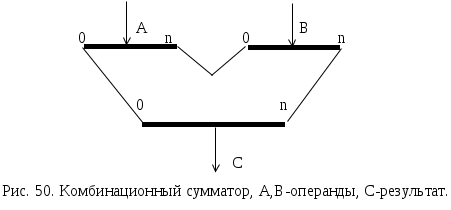 Накапливающим называется сумматор, который осуществляет сложение слов A и B при подаче их на сумматор одного за другим. В накапливающем сумматоре имеется дополнительный регистр для хранения результата. 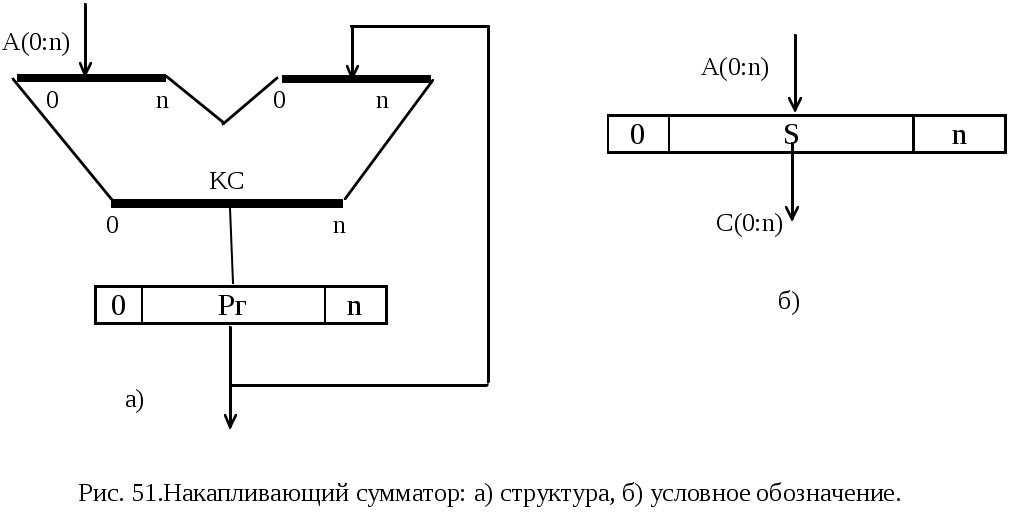 Структура и условное обозначение накапливающего сумматора представлены на рис. 51. Счетчик - операционный элемент, который реализует микрооперацию счета. Микрооперация счета состоит в изменении состояния счетчика (значения хранимого слова) на 1. Кроме того счетчик может выполнить и такие микрооперации: установка в 0 и прием произвольного числа. Т.е. полный набор возможных микроопераций для счетчика: 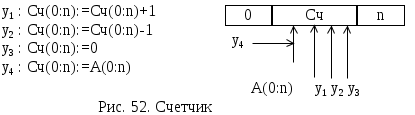 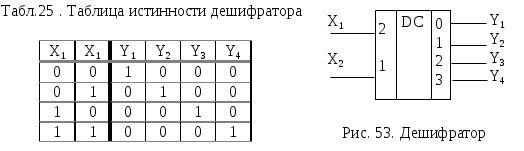 Счетчик, выполняющий микрооперацию у1 называется суммирующим, микрооперацию у2 - вычитающим, обе микрооперации - реверсивный. Дешифратор - операционный элемент, выполняющий функцию преобразования некоторого n-разрядного двоичного кода в унитарный код «один из N». Если N=2n - то такой дешифратор называется полным, если N<2n - то частичным. Таблица истинности простейшего полного дешифратора (n=2) и его условное обозначение приведены в табл. 25. и на рис. 53. Промышленность может выпускать дешифраторы с инверсными выходами. Для такого дешифратора таблица истинности и условное обозначение имеют вид (табл. 26., рис. 54.) 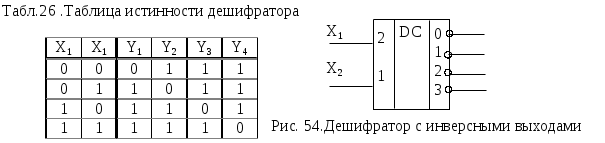 СИНТЕЗ МИКРОПРОГРАММНЫХ АВТОМАТОВ ПО ГРАФ-СХЕМЕ АЛГОРИТМА Граф-схема алгоритма есть форма представления микропрограммы, которую должно выполнить операционное устройство (ОУ). При построении операционного устройства, как состоящего из операционного (ОА) и управляющего (УА) автоматов, необходимо уметь выделить функции ОА и УА из ГСА. Обычно микропрограмма представляется в виде содержательной ГСА. В этом случае для задания функций ОА необходимо перечислить все выполняемые микрооперации и все проверяемые логические условия данной микропрограммы, а также описать разрядность слов, обрабатываемых операционным устройством. На основании этих данных можно построить ОА методами, которые будут изложены в курсе «Схемотехника ЭВМ». Для инициализации выполнения той или иной микрооперации на ОА должны поступать в нужный согласно ГСА момент времени управляющие сигналы Yi. Обычно при проектировании ОУ принимают определенный способ кодирования микроопераций (чаще всего кодом, содержащим столько разрядов, сколько всего различных микроопераций) и для разработки ОА считают, что УА выдает код микроопераций, которые должны выполниться в данный момент времени. Для УА важна последовательность выдачи соответствующих кодов микроопераций в зависимости от логических условий, вырабатываемых ОА и анализируемых УА в нужные моменты времени. Если принят способ кодирования микроопераций, то функции УА задаются кодированной ГСА. Поэтому для различных содержательных ГСА , имеющих одинаковую кодированную ГСА, ОА будут различны, но УА будет одним и тем же. В дальнейшем будем рассматривать синтез только УА и только кодированной ГСА. Конечный автомат, интерпретирующий микропрограмму работы дискретного устройства, называется микропрограммным автоматом. Одну и ту же ГСА можно интерпретировать как автоматом Мили, так и автоматом Мура. Абстрактный синтез микропрограммного автомата по ГСА осуществляется в два этапа: 1. Получение отмеченной ГСА. 2. Построение графа автомата или таблиц переходов и выходов. СИНТЕЗ АВТОМАТА МИЛИ На этапе получения отмеченной ГСА входы вершин, следующих за операторными, отмечают символами a1, a2,.. по следующим правилам: 1) символом а1 отмечают вход вершины, следующей за начальной, а также вход конечной вершины; 2) входы всех вершин следующих за операторными, должны быть отмечены; 3) входы различных вершин, за исключением конечной, отмечаются различными символами; 4) если вход вершины отмечается, то только одним символом. Ясно, что для проведения отметок потребуется конечное число символов а1,...,am. Результатом первого этапа является отмеченная ГСА, которая служит основой для второго этапа - перехода к графу или таблицам переходов-выходов. Пример ГСА, отмеченной для автомата Мили, представлен на рис. 55. 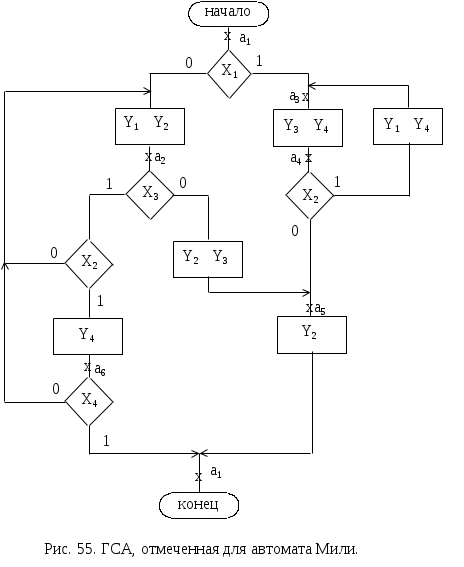 На втором этапе, из отмеченной ГСА, строят граф автомата или таблицы переходов-выходов. Для этого полагают, что в автомате будет столько состояний сколько символов ai понадобилось при отметке ГСА. На плоскости рисунка отмечаем все состояния автомата ai. Для каждого из состояний ai определяем по отмеченной ГСА все пути, ведущие в другие состояния и проходящие обязательно только через одну операторную вершину. Например, из состояния а1(рис.55.) есть переход в состояние a2 (путь проходит через операторную вершину y1 y2) и в состояние a4 (путь проходит через вершину y3 y4). Перехода из a1 в a3 нет, так как на этом пути нет ни одной операторной вершины. Будем считать, что автомат осуществляет переход, например, из a1 в a2 при условии x1 = 0 или x1 (см.ГСА, рис.55. ) и вырабатывает на этом переходе выходные сигналы у1 у2 (то, что записано в проходимой операторной вершине ГСА, рис.55.). Значение условий х2, х3, х4 на этом переходе не оказывает влияния на автомат. И  сключение составляет только путь, ведущий в конечную вершину, он может не содержать ни одной операторной вершины (например, переход из а6 в а1), т.е. не сопровождается выработкой выходных сигналов.Отмечаем на графе все указанные пути для всех состояний в виде дуг, которым приписываем условия перехода и выходной сигнал, вырабатываемый на этом переходе. Получим граф автомата (рис.55. ). 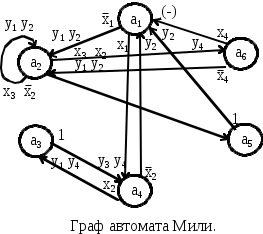 На этом графе переходам типа а3 a4, a5 a1 приписывается условие перехода 1, т.к. эти переходы являются безусловными и выполняются всегда, когда автомат попадает в состояние а3 (или а5). На основании отмеченной ГСА или графа автомата можно построить таблицу переходов-выходов. Для микропрограммных автоматов таблица переходов-выходов строится в виде списка и различаются прямая и обратная таблицы. Для данного автомата прямая таблица представлена в табл. 27., обратная - в табл. 28. Табл. 27.Прямая таблица переходов- Табл. 28.Обратная таблица перехо- выходов автомата Мили дов - выходов автомата Мили
В приведенных таблицах am - исходное состояние, aS - состояние перехода, Х - условие (входной сигнал), обеспечивающий переход из состояния am в состояние as, Y - выходной сигнал, вырабатываемый автоматом при переходе из am в aS. СИНТЕЗ АВТОМАТА МУРА. Для автомата Мура на этапе получения отмеченной ГСА разметка производится согласно следующим правилам: 1) символом а1 отмечается начальная и конечная вершины; 2) различные операторные вершины отмечаются различными символами; 3) все операторные вершины должны быть отмечены; Пример ГСА, отмеченной для автомата Мура, представлен на рис. 56. 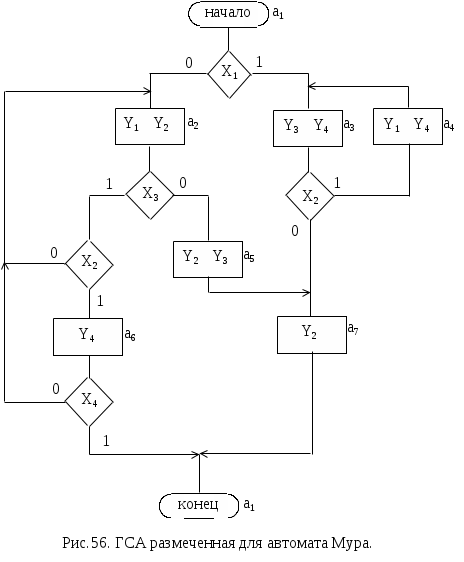 Граф автомата Мура, соответствующий отмеченной ГСА (рис. ), представлен на рис. . Построение его аналогично построению графа для автомата Мили. |