Глава 2.Ненаправленные графы, часть 1. Простые графы (графы) Способы задания графа Основные способы задания графов графический

• Название: Простые графы (графы) Способы задания графа Основные способы задания графов графический
• Анкор: Глава 2.Ненаправленные графы, часть 1.doc
• Дата: 04.09.2018
• Размер: 1.28 Mb.
• Имя файла: Глава 2.Ненаправленные графы, часть 1.doc
• Тип: Глава; #24055
• страница: 6 из 14

2.3.4. Граф звезда

Определения

Граф звезда является деревом на (n+1) вершине, из которых одна является смежной n вершинам, а остальные вершины имеют степень 1. Граф звезда имеет специальное обозначение S_n.

Пример

Рис.2.3.5. Примеры графов звезда

2

Определения

.3.5. Граф шина


Шина - граф G, имеющий n вершин и (n-1) ребер, при этом n-2 вершины имеют степень 2, а две вершины – степень 1.

Пример

Рис.2.3.6. Граф шина

2.3.6. Граф цикл

Определения

Г

Пример

раф с n вершинами степени 2 и n рёбрами (имеет специальное обозначение C_n) такой, что вершина i соединена с двумя вершинами i+1 и i-1.








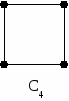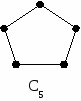
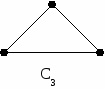
Рис.2.3.7. Пример графов цикл (кольцо)

1.3.7. Граф колесо

Определения

Граф колесо порядка n (обозначается W_n) имеет одну вершину степени n-1, а остальные вершины имеют степени 3. (Вершина степени n-1 часто называется хабом (hub)).

Пример

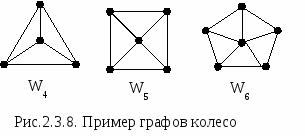
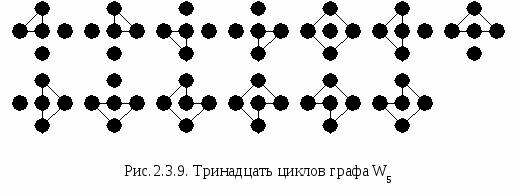
Данные графы интересны тем, что число циклов в графе W_n равно n²-3n+3. Например, для W₄ число циклов равно 13.

Пример

2.4. Изоморфизм графов

Определения

Два графа могут быть одинаковыми во всем, кроме имен вершин (например, G₁=(V,E), G₂=(U,E), |V|=|U|). В этом случае говорят об изоморфизме графов.

Формально, графы G и H являются изоморфными, если существует соответствие один к одному вида

f: V(G)  V(H) такое, что

{ V_j,V_k }E(G)  f{V_j}f{V_k}E(H)

Функция f называется изоморфизмом.

Пример

1


2

1





3

5

3





4


4

2


5


6


6

Рис.2.4.1. Два изоморфных графа

Класс сложности

Неизвестен алгоритм нахождения изоморфизма графов общего вида в полиномиальное время, но не доказано, что проблема является NP-полной. Некоторые авторы выделяют отдельный класс сложности изоморфизма графов.

Алгоритмы полиномиального времени

Существуют алгоритмы нахождения изоморфизма в полиномиальное время для частных случаев графов (планарных графов, графов с ограниченными степенями вершин и некоторых других).

Классификация алгоритмов

Алгоритмы распознавания изоморфизма графов:

• 
  прямые переборные алгоритмы;
  
• 
  алгоритмы направленного перебора;
  
• 
  непереборные алгоритмы.
  

Перебор убыстряется с использованием:

• 
  инвариантов;
  
• 
  системы инвариантов.