Глава 2.Ненаправленные графы, часть 1. Простые графы (графы) Способы задания графа Основные способы задания графов графический
 Скачать 1.28 Mb. Скачать 1.28 Mb.
|
2.2.3. Унарные операции над графами Для графа G=(V,E) частью графа называется такой граф H=(V’,E’), у которого V’(H)V(G) и E’(H)E(G). Другими словами, этот граф, порожденный ребрами графа G. Частью графа является путь, цикл и т.п. Вместо термина «часть графа» часто используют термин «подграф (в слабом смысле)». Подграф ( в сильном смысле)- для графа G=(V,E) такой граф H=(W,U), у которого множество вершин W Если G1G и G1 содержит все вершины графа G, тогда G1 называют каркасным подграфом. Каркасных подграфов может быть несколько. Дополнением графа G=(V,E) называется граф G’=(V,E’), у которого:
Пример 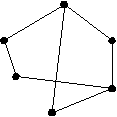 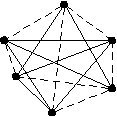 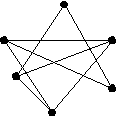 G G’ Рис.2.2.5. Граф G и его дополнение G’ Определение Операцией декомпозиции графа G(V,E) называется представление его в виде последовательности графов G1,…, GS таких, что:
E(G)= Замечания
Определение Операция построения реберного графа L(G)=(U,F) графа G=(V,E) состоит в следующем:
 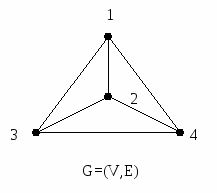 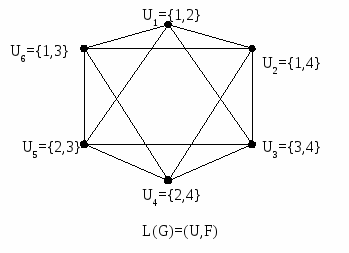 е1 е6 е2 е4 е5 е3 Вершины L(G): U1={1,2}, U2={1,3}, U3={1,4}, U4={2,3}, U5={2,4}, U6={3,4} Ребра L(G) (определяются в соответствии со вторым условием): 1 ребро L(G) ребра {1,2}и{1,3} смежны в G: U1 соединена ребром с U2 2 ребро L(G) ребра {1,2}и{1,4} смежны в G: U1 соединена ребром с U3 3 ребро L(G) ребра {1,2}и{2,4} смежны в G: U1 соединена ребром с U5 4 ребро L(G) ребра {1,2}и{2,3} смежны в G: U1 соединена ребром с U4 5 ребро L(G) ребра {1,2}и{1,3} смежны в G: вариант был 6 ребро L(G) ребра {1,3}и{1,4} смежны в G: U2 соединена ребром с U3 7 ребро L(G) ребра {1,3}и{2,3} смежны в G: U2 соединена ребром с U4 8 ребро L(G) ребра {1,3}и{3,4} смежны в G: U2 соединена ребром с U6 9 ребро L(G) ребра {1,4}и{1,2} смежны в G: вариант был 10 ребро L(G) ребра {1,4}и{1,3} смежны в G: вариант был 11 ребро L(G) ребра {1,4}и{2,4} смежны в G: U3 соединена ребром с U5 12 ребро L(G) ребра {1,4}и{3,4} смежны в G: U3 соединена ребром с U6 13 ребро L(G) ребра {2,3}и{1,3} смежны в G: вариант был 14 ребро L(G) ребра {2,3}и{1,2} смежны в G: вариант был 15 ребро L(G) ребра {2,3}и{2,4} смежны в G: U4 соединена ребром с U5 16 ребро L(G) ребра {2,3}и{3,4} смежны в G: U4 соединена ребром с U6 17 ребро L(G) ребра {3,4}и{1,3} смежны в G: вариант был 18 ребро L(G) ребра {3,4}и{2,3} смежны в G: вариант был 19 ребро L(G) ребра {3,4}и{1,4} смежны в G: вариант был 20 ребро L(G) ребра {3,4}и{2,4} смежны в G: U5 соединена ребром с U6                 Определения Срединный граф M(G) получается из графа G выполнением следующих операций:
Тотальный граф T(G) графа G строится следующим образом:
k-ой степенью Gkграфа G=(V,E) является граф с тем же множеством вершин V(G) и ребром между двумя вершинами тогда и только тогда, когда между ними имеется путь длиной самое большее k. 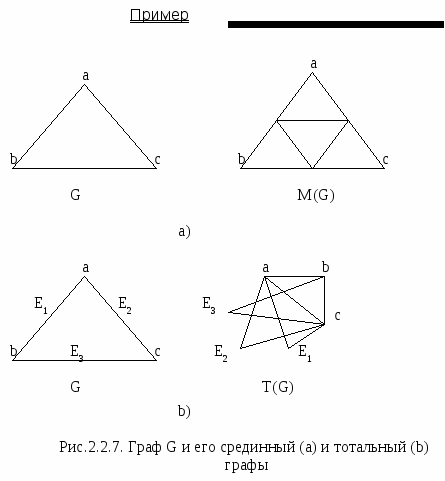 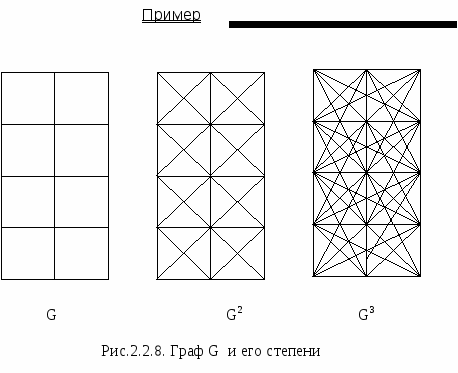 |

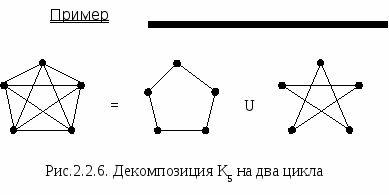 перация объединения раздельных графов является операцией, обратной операции декомпозиции.
перация объединения раздельных графов является операцией, обратной операции декомпозиции.