Глава 2.Ненаправленные графы, часть 1. Простые графы (графы) Способы задания графа Основные способы задания графов графический

• Название: Простые графы (графы) Способы задания графа Основные способы задания графов графический
• Анкор: Глава 2.Ненаправленные графы, часть 1.doc
• Дата: 04.09.2018
• Размер: 1.28 Mb.
• Имя файла: Глава 2.Ненаправленные графы, часть 1.doc
• Тип: Глава; #24055
• страница: 2 из 14

2.1.4. Последовательность степеней вершин графа

Определения

Последовательностью степеней вершин графа G является последовательность его степеней, записанная в порядке возрастания степеней с повторами.

С помощью последовательности степеней графа можно задавать сам граф, но не всегда однозначно.

Определения

Последовательность d₁,d₂,…,d_n неотрицательных целых чисел называется графической, если она представляет последовательность степеней графа.

Из леммы рукопожатий следует, что если последовательность неотрицательных чисел является графической, то сумма элементов в этой последовательности четна. Для простых графов наибольший элемент графической последовательности неотрицательных чисел равен n-1.

Теорема Havel - Hakimi

П

Замечания

оследовательность d₁≥ d₂≥ …≥d_n≥0 неотрицательных целых чисел является графической тогда и только тогда, когда последовательность d₂ –1, d₃ – 1, …, d_k+1, d_k+2, d_k+3,…,d_n (k=d₁) является графической.



1. Важно отметить, что описатели d_i являются только описателями последовательности. Запись последовательности в таком виде не означает, что вершины есть {1,2,..,n} и что d₁ является степенью вершины 1 и т.д.

2. Теорема говорит, что если заданная последовательности является графической, то она может быть реализована в виде графа, в котором вершина степени d₁ смежна с вершинами степени d₂, d₂,…, d_k+1 (k= d₁). Это утверждение задает правило построения графа по последовательности:

если был построен граф с n-1 вершинами и последовательностью степеней d₂ –1, d₃ – 1, …, d_k+1, d_k+2, d_k+3,…,d_n (k=d₁), то добавляется новая вершина и соединяется с вершинами степени d₂ –1, d₃ – 1, …, d_k+1-1, (k=d₁).

2.1.5. Матричный способ задания графов

Определения

Матрица инциденций

Простому графу G можно сопоста­вить матрицу инциденций [B]: прямоугольную матрицу размерности mxn, строки которой соответствуют вершинам, а столбцы - рёбрам графа.

Элемент матрицы инцидентности в i-ой строке и j-ом столбце равен числу раз инцидентности i-ой вершины и j-ого ребра.

Для простого графа матрица инциденций имеет вид:






Строки матрицы инциденций [B] называют векторами инциденций графа G.

Свойства матрицы инциденций:

1. Количество единиц в строке равно степени deg (V_i);

2. Количество единиц в столбце графа равно 2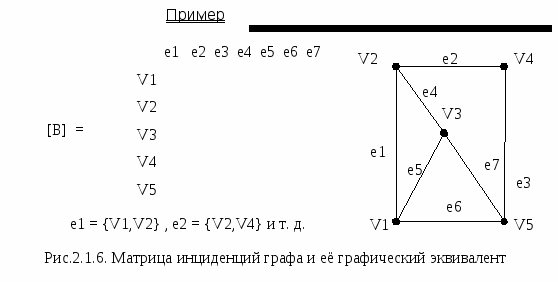

Матрица смежности

Матрица смежности вершин графа (или просто матрица смежности) [A] – квадратная матрица n×n, строки и столбцы которой соответствуют вершинам графа.

Элемент матрицы смежности для i-ой строки и j-го столба равен числу ребер между i-ой и j-ой вершинами.

Элементы матрицы [A] простого графа равны:

[A] =

Свойства матрицы смежности:

1. Для простого графа матрица смежности симметрична относительно главной диагонали

2. 
   Для простого графа главная диагональ - нулевая.
   

С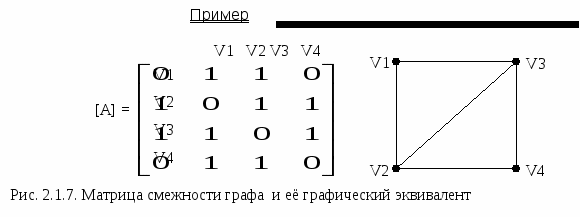праведливо следующее ут­верждение: Любой симметричной матрице с элементами множества {0,1} можно поставить в соответствие граф.

Матрица Лапласа (Кирхгоффа)

Матрицей Лапласа графа G является квадратная матрица [L] порядка [nn], где n – число вершин.

Элементы матрицы [L] равны:



Матрица Лапласа [L] и матрица смежности [A] графа G связаны между собой:

[L] = [D] - [A],

где [D] – диагональная матрица, элементы d_ii которой равны степеням вершин V_i.

Пример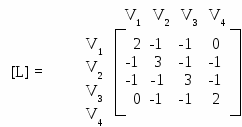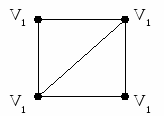

Рис.2.1.8. Матрица Лапласа графа G