|
Глава 2.Ненаправленные графы, часть 1. Простые графы (графы) Способы задания графа Основные способы задания графов графический
2.5.1.Вершинно- и реберно-независимые пути
Определения

Пути между двумя заданными вершинами u и v графа G называются:
вершинно-независимыми(вершинно-разделенными), если они не имеют общих вершин, за исключением u и v;
р Меры еберно-независимыми (реберно-разделенными), если они не имеют общих ребер.

Расстояние аварии (ошибки) – длина вершинно-независимого пути в графе.
Диаметр аварии (ошибки) – максимальный среди всех вершинно-независимых путей между двумя вершинами.
Между двумя различными вершинами графа G(V,E) имеется по крайней мере (G) вершинно-независимых путей и по крайней мере (G) реберно-независимых путей.
2.6. Связность
Определения

Непустой граф G называется связным, если любые его вершины могут быть соединены путем.

(G) – вершинная связность. Измеряется наименьшим числом вершин, удаление которых приведет к несвязному или одновершинному графу.
(G) – реберная связность: наименьшее число ребер, удаление которых приводит к несвязному графу.

2
5
4
8
6
1
7
3
Рис.2.6.1. Связный граф
Теорема Уитни

Если (G) – минимальная степень вершин графа G, то справедливо неравенство
(G) (G) (G)
Определения

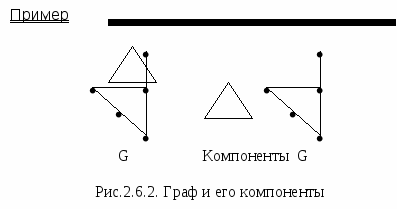
Пусть G=(V,E) будет графом. Тогда максимальный (т.е. имеющий наибольшее число вершин и/или ребер) связный подграф графа G называется компонентой графа G.
Заметим, что компонента, будучи связной, всегда является не пустой; пустой граф вообще не имеет компонент.
Теоремы
 Теорема 1

Любой граф с n вершинами, имеющий более чем (n-1)(n-2)/2 ребер, связан.
Теорема 2

Граф будет связным тогда и только тогда, когда он имеет одну компоненту. Граф будет не связным тогда и только тогда, когда он имеет по меньшей мере две компоненты.
Теорема 3

Пусть G=(V,E) будет графом с n вершинами и k компонентами. Тогда число m его ребер удовлетворяет условию
n-k m (n-k)(n-k+1)/2
Класс сложности

Определение связности графа требует линейного времени.
Алгоритмы

Алгоритм обхода графа в глубину (DFS) позволяет ответить на вопрос, является ли граф связным. Для этого необходимо:
Установить, что все вершины не маркированы (являются белыми);
Начиная с любой вершины, выполнить алгоритм обхода в глубину (DFS);
Если после выполнения алгоритма поиска в глубину остались немаркированными вершины, то граф является несвязным. В противном случае – граф связный.
Алгоритм обхода графа в ширину также отвечает на вопрос о связности графа в линейное время.
|
|
|
 Скачать 1.28 Mb.
Скачать 1.28 Mb.