Глава 2.Ненаправленные графы, часть 1. Простые графы (графы) Способы задания графа Основные способы задания графов графический

• Название: Простые графы (графы) Способы задания графа Основные способы задания графов графический
• Анкор: Глава 2.Ненаправленные графы, часть 1.doc
• Дата: 04.09.2018
• Размер: 1.28 Mb.
• Имя файла: Глава 2.Ненаправленные графы, часть 1.doc
• Тип: Глава; #24055
• страница: 11 из 14

2.7. Деревья. Каркасные деревья.

Множество фундаментальных циклов

Определения

Граф G называется деревом, если он связан и не содержит циклов.

Существует несколько эквивалентных определений дерева.

Теорема

Пусть G(V,E) будет деревом с |V| = n. Тогда следующие определения эквивалентны:

• 
  G является деревом, если он связан и не содержит циклов.
  
• 
  G является деревом, если он не содержит циклов и имеет n-1 ребер.
  
• 
  G является деревом, если он связан и раждое ребро является ребром разреза (мостом).
  
• 
  G является деревом, если две любые вершины G соединены между собой точно одним путем.
  
• 
  G является деревом, если граф не имеет циклов, но добавление одного ребра создает ровно один цикл.
  

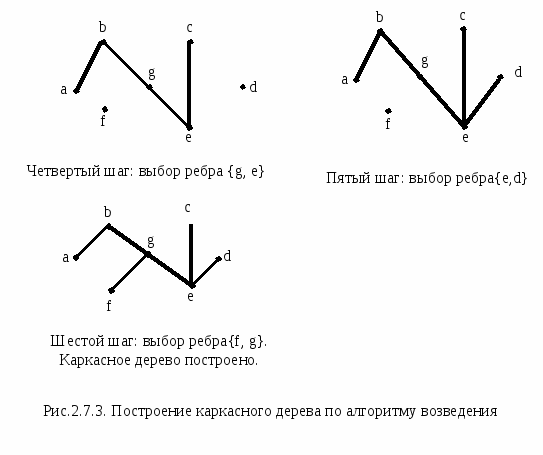
Примеры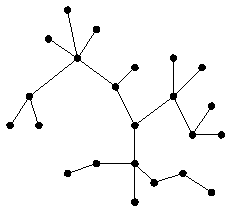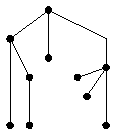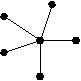

Рис.2.7.1. Деревья

Определения

Вершины дерева степени 1 являются его листьями.

Граф без циклов будет лесом. Лес состоит из деревьев.

Иногда удобно рассматривать одну из вершин как специальную вершину. Такая вершина называется корнем дерева. Дерево с такой вершиной является корневым деревом.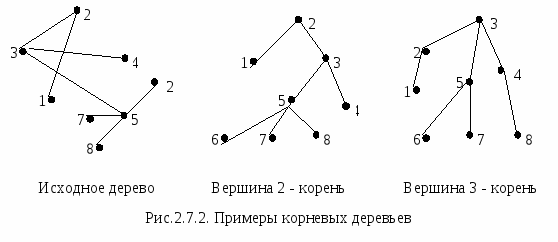

Определения

Пусть G = (V,E) будет простым графом. Каркасное дерево для G будет деревом T=(V,E¹) с множеством вершин V и множеством ребер E¹ E.

Примеры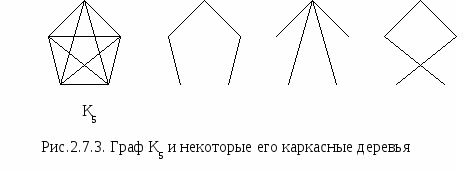

Теоремы

Теорема 1

Каждый связной граф имеет по меньшей мере одно каркасное дерево.

Теорема Кирхгоффа

(Matrix-Tree Theorem)

Пусть G=(V,E), n=|V(G)|, V(G)= {v₁,…,v_n}, будет простым графом. Матрица Лапласа размера n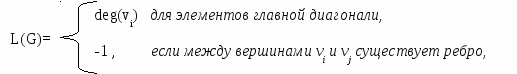n определяется следующим образом:



где deg(v_i) – степень вершины v_i.

Редуцированной матрицей Лапласа L^i,j(G) будет матрица размера (n-1)=(n-1) будет матрица, полученная из матрицы Лапласа удалением i-ой строки и j-го столбца.

Тогда число каркасных деревьев графа G=(V,E) равно

(-1)^i+j detL^i,j(G),

где detL^i,j(G) – детерминант редуцированной матрицы Лапласа L^i,j(G).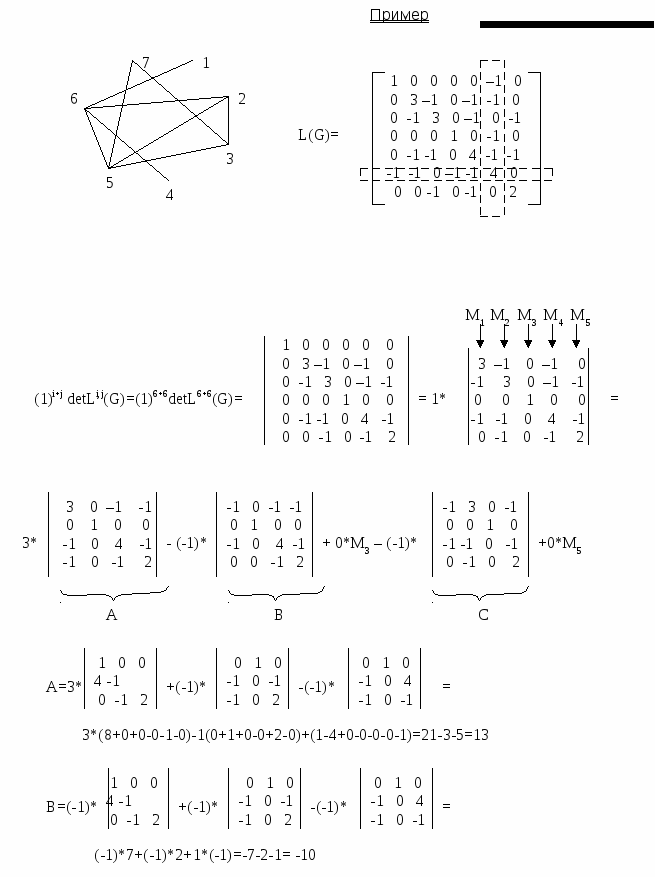




Редуцированная матрица Лапласа получается из матрицы Лапласа вычеркиванием 6-го столбца и 6-ой строки (для уменьшения числа вычислений берутся столбец и строка с наибольшим числом ненулевых элементов).

Точный алгоритм нахождения

каркасного дерева графа

При любом исполнении алгоритма поиска в глубину (DFS) изменение цвета вершин идет вдоль каркасного дерева, следовательно запись порядка прохождения вершин в DFS даст запись каркасного дерева (см.п.1.8.).

Простые алгоритма нажодения каркасного дерева

Э

Алгоритм возведения

ти алгоритмы применимы лишь для графов совсем небольших размеров из-за трудностей нахождения циклов.

1. 
   Выбирать ребра графа один за другим так, чтобы не создавать циклов.
   
2. 
   Повторять 1 до тех пор, пока в дерево не будут включены все вершины.
   

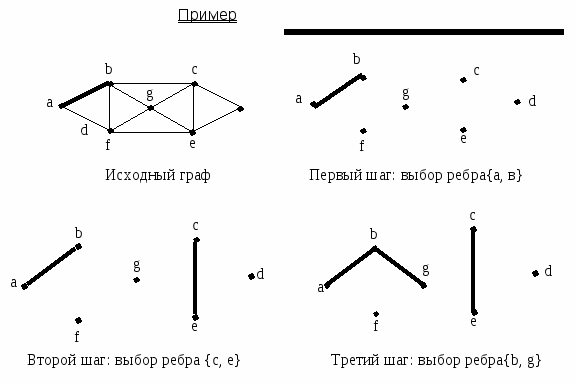Алгоритм вырезания

Выбрать любой цикл в неграфе и удалить одно ребро.

Повторять 1 до тех пор, пока в графе не останется циклов.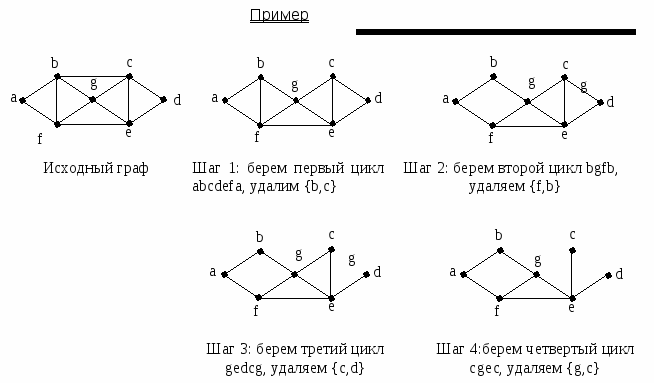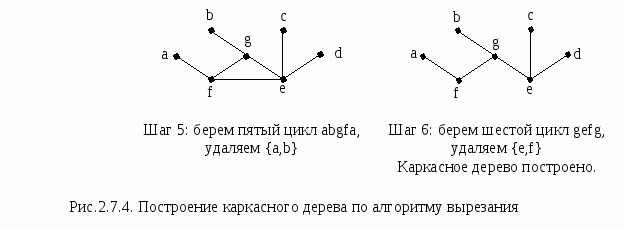

Определения

Каркасное дерево T=(V,E¹) связного простого графа G=(V,E), |V|=n, |E|=m, содержит n-1 ребро. Каждое ребро, не принадлежащее каркасному дереву T=(V,E¹), порождает в точности один цикл при добавлении его к T. Такой цикл является элементом множества фундаментальных циклов графа G относительно каркасного дерева T.

Поскольку каркасное дерево имеет n-1 ребро, в фундаментальном множестве циклов графа G относительно каркасного дерева T имеется m-n=1 циклов (|V|=n, |E|=m).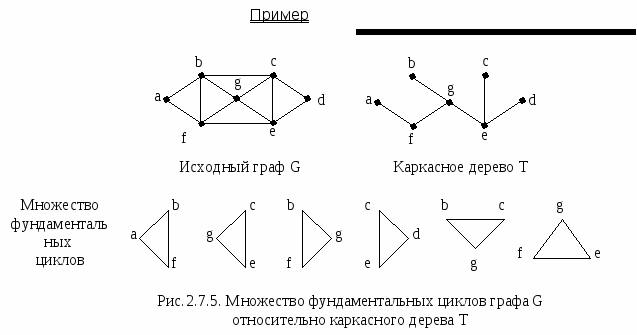

Определения

Если ребра графа G обозначены e₁,e₂,…,e_m, а фундаментальные циклы – Σ_i, i=1,2,…,k, то элементы матрицы фундаментальных циклов С=(с_ij)_kxm определяются следующим образом:


1, если Σ_i содержит ребро e_j

c_{ij =}

0 в остальных случаях

Пример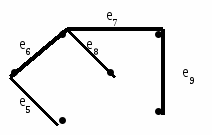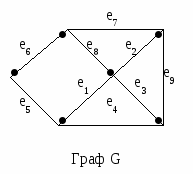

Множество фундаментальных

циклов

Σ₁ = {e₁,e₅,e₆,e₈}

Σ₂ = {e₂,e₇,e₈}

Σ₃ = {e₂,e₃,e₉}

Σ₄ = {e₁,e₃,e₄}


Каркасное дерево T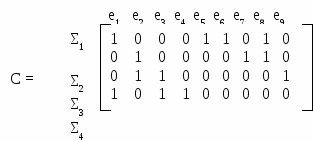





μ = 9-6+1= 4

Рис.2.7.6. Граф G и его матрица фундаментальных циклов

Определения

Пространством циклов называется множество всех простых циклов графа G. Множество фундаментальных циклов неоргафа G относительно каркасного дерева T образует базис пространства циклов.

Это означает, что все другие циклы графа G могут быть получены линейной комбинацией (операцией по модулю 2 – mod₂) фундаментальных циклов графа G относительно каркасного дерева T.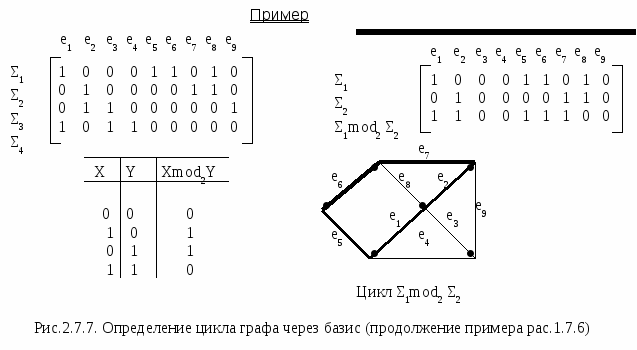

Меры

• 
  μ - цикломатическое число графа G, равное размеру пространства циклов.