|
Глава 2.Ненаправленные графы, часть 1. Простые графы (графы) Способы задания графа Основные способы задания графов графический
2 Определения .8. Обход графа

Обходом графа является последовательность вершин графа, в которой каждая вершина содержится ровно один раз.
Наиболее общие алгоритмы обхода графов:
Обход в глубину (Deph-First Search – DFS);
Обход в ширину (Breadth-First Search – BFS).
2 Определения .8.1..Обход в глубину (DSF)

Обход в глубину является алгоритмом систематического посещения (прохождения) вершин графа, состоящего из двух движений:
вперед (к еще непосещенной вершине) всегда, когда это возможно;
возврат от текущей вершины по пройденному ребру назад (к ранее пройденной вершине), если движение вперед от текущей вершины невозможно.
После завершения обхода в глубину все ребра связанного графа оказываются разбитыми на два класса:
ребра дерева, по которым осуществлялись впереходы из посещенных вершин в непосещенные;
ребра касания, замыкающие циклы графа.
Частичный граф, порожденный ребрами дерева, называется деревом обхода в глубину. Этот граф является каркасным графом исходного графа.

Введем три основных атрибута алгоритма DFS:
1) Раскрашивание вершин. При выполнении алгоритма DFS вершины раскрашиваются в зависимости состояния вершины.

Раскрашивание вершин – это своебразная память (похоже на расбрасывание крошек хлеба в лабиринте – по ним можно определить местоположение в лабиринте).
2) Поддержка времени. Каждая вершина u имеет два времени: время обнаружения d[u] и время завершения f[u]. Время обнаружения соответствует моменту изменения белого цвета на серый, а время завершения – изменению серого цвета на черный. Время начинается с 1 , и с каждой отметкой события (обнаружение или завершение) время увеличивается на единицу.
3) Вершины-предшественники и DFS-дерево. Для каждой пройденной вершины в специальный массив записывается вершина-предшественник: p[u]=v. Это позволяет организовать обратное движение алгоритма.
Каждый связанный компонент графа может быть превращен в дерево удалением некоторых ребер. Каждая вершена u в дереве будет иметь указатель на своего предшественника (родителя) p[u], создавая таким образом дерево предшественник-указатель.
Псевдокод

Инициализация и начало алгоритма
Для всех вершин u делать
{ цвет {u}=белый;
p[u]=NULL;
}
Время=0;
Для всех вершин u делать
Если цвет [u]=белый, тогда DFS;
Алгоритм DFS
DFS:
Посетить (u);
Время=Время+1;
d[u]=Время;
цвет[u]=серый;
Для всех v, инцидентных u, делать
{ если цвет[v]= белый, тогда
{p[v]=u;
DFS{u};
{
{
Время=Время+1;
f[u]=время;
цвет[u]черный;
Класс сложности

Сложность адгоритма DFS – O(n+m), где n=|V|, m=|E|, т.е.проблема относится к P классу.

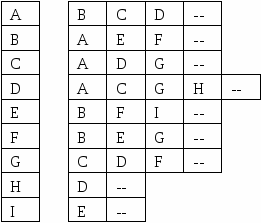
Задан граф и его таблица инцидентности:
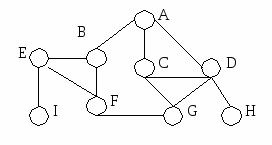
Номер
шага
Рисунок графа
Описание действий
алгоритма DFS

1
Обход в глубину начинается с вершины I.
d[I]=1 (отмечено на рис.).
Вершина I на рисунке и в таблице инцидентности помечается серой.
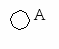 
   

2
По таблице инцидентности определя-
ем вершины, инцидентные I. Такой вершиной является E. Переход в E.
d[E]=2, p[E]=I.
Вершина E на рисунке и в таблице инцидентности помечается серой.
   
   

3
По таблице инцидентности вершина E имеет две белые инцидентные вершины B и F. Случайно B выбирается первой.
d[B]=3, p[B]=E.
Вершина B на рисунке и в таблице инцидентности – серая.
E
2


4-6
Подобным образом помечаются вершины A,C,D.
d[A]=4; d[C]=5; d[D]=6;
p[A]=B; p[C]=A; p[D]=C.
Вершины A,C,D становятся серыми
A
4

E
2
C
5
    


7-8
Вершина D имеет 4 инцидентных вершины: A,C,G,H. Вершины A и C являются серыми, поэтому выбирается вершина G.
d[G]=7, p[G]=D.
Затем выбирается вершина F:
d[F]=8, p[F]=G.
Вершины G и F помечаются серыми.
A
4

E
2
C
5
    


9
A
4
Все вершины, инцидентные F, являются серыми. Поэтому алгоритм начинает обратное движение. По p[F] предшественником является вершина G. Переходим в эту вершину.
Вершина F – черная.
f[F]=9 (отмечено жирной цифрой).
E
2
C
5
 
   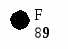



10
Все вершины, инцидентные G либо серые, либо черные. Вершина G становится черной.
f[G]=10 (помечено жирной цифрой)
A
4

 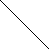 
E
2
 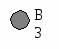 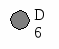
C
5
    
   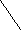 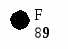
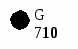 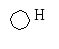 


A
4
11
Вершине G предшествовала вершина
D (p[G]=D). Возврат в вершину D. Имеется белая вершина H, инцидентная D.
d[H]=11, p[H]=D.
Вершина H - черная
E
2
C
5
 
   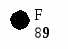


12-18
Вершина D, инцидентная H,серая. Поэтому начинается обратных обход.
Вершина H становится черной.
f[H]=12.
Оставшиеся вершины посещаются в обратном поряке согласно массива предшественнов.
Поочередно вершины становятся черными:
f[D]=13, f[C]=14, f[A]=15, f[B]=16, f[E]=17, f[I]=18 (отмечены жирным шрифтом)
 
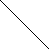 
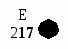 
 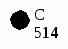
   
    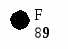
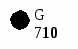  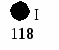


Раскраска таблицы инцидентности после 10 шагов:
A
B
C
D
--
A
B
C
D
--
B
A
E
F
--
B
A
E
F
--
C
A
D
G
--
C
A
D
G
--
D
A
C
G
H
--
D
A
C
G
H
--
E
I
F
B
--
E
I
F
B
--
E
B
F
G
--
E
B
F
G
--
F
D
C
G
--
F
D
C
G
--
D
H
--
D
H
--
E
I
--
E
I
--
Дерево предшественник-указатель (или дерево обхода в глубину):
A
 
B

E
Все остальные ребра графа, не вошедшие в это дерево, являются ребрами касания

D

C
  
G
H
I
F

   
|
|
|
 Скачать 1.28 Mb.
Скачать 1.28 Mb.