Глава 2.Ненаправленные графы, часть 1. Простые графы (графы) Способы задания графа Основные способы задания графов графический
 Скачать 1.28 Mb.
|
2.6.1. Реберная связностьОпределения Введем следующую запись: если G есть граф и {vi ,vj}-его ребро, то будем записывать G-{vi ,vj}граф, полученный из исходного графа G удалением ребра {vi ,vj}. Формально вновь полученный граф имеет множество вершин V(G) и множество ребер E(G) -{vi ,vj}. Ребро {vi ,vj}  E(G) называется ребром разреза (или мостом), если G-{vi ,vj}имеет больше компонентов, чем исходный граф G. Обобщением понятия ребра разреза (моста) является понятие разрывающего множества ребер S графа G=(V,E). Это – такое множество, что граф H=(V, E-S) имеет меньше компонент, чем граф G=(V,E). Граф называется k-связным (или k-реберносвязным) у, если λ(G)  k.Теорема Ребро а графа G является мостом тогда и только тогда, когда а не принадлежит ни к одному циклу графа. Примеры a 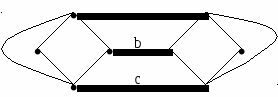 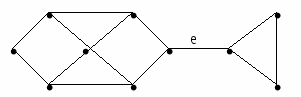 Рис.2.6.3. Ребро разреза e Рис.2.6.4. Разрывающее множество ребер a,b,c Класс сложности Нахождение числа реберной связности λ(G) относится к классу NP-тяжелых. 2.6.2. Вершинная связностьОпределения Граф G называется k-вершинносвязным, если κ(G)  k.В графе может существовать вершина, удаление которой вместе с инцидентными ей ребрами разъединяет оставшиеся вершины. Такая вершина называется точкой сочленения или разделяющей точкой. Граф, содержащий точку разделения, будет разделимым. Граф без точек сочленения называется двусвязным или неразделимым. Максимальный двусвязный подграф графа является двусвязной копонентой или блоком. Пример 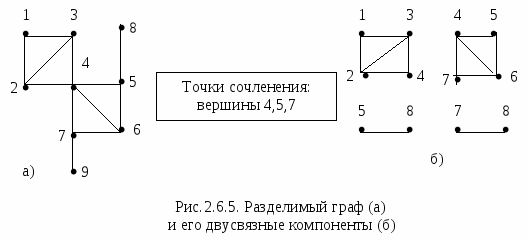 Класс сложностиНахождение числа вершинной связности κ(G) относится к классу NP-тяжелых.
Определение Вершинно-реберным разделяющим множеством связного графа G называется множество вершин и ребер (содержащее хотя бы одну вершину и одно ребро) графа G, при удалении которых получается либо несвязный граф, либо одновершинный граф. Меры
Класс сложностиНахождение числа вершинно-реберной связности κγ (G) относится к классу NP-тяжелых. 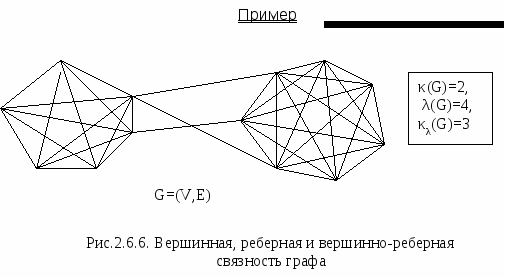 Следствие 2ТеоремаСледствие 1 Для любого связного графа G λ(G)>1 κ(G) κλ(G) λ(G). Для любого связного графа G, если λ(G)=1, то κλ(G) либо не определено, либо κλ(G)> λ(G).  Для полного графа Kn (n 3) λ(Kn)= κ(Kn)= κλ(Kn)=n-1 .Следствие 3Для цикла Cn (n 3) λ(Cn)= κ(Cn)= κλ(Cn)=2 |