|
Глава 2.Ненаправленные графы, часть 1. Простые графы (графы) Способы задания графа Основные способы задания графов графический
2.3.1. Изоморфизм графов и прямые методы п Определение еребора

П Замечание усть G1 и G2 будут графами, а А1 и А2 – их матрицами смежности. Графы G1 и G2 будут изоморфными, если их матрицы смежности равны.
Задача определения равенства матриц смежности сложна, т.к. вид матрицы смежности графа зависит от процедуры именования вершин графа.
Пример

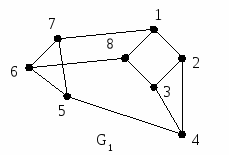 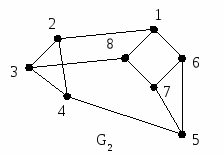
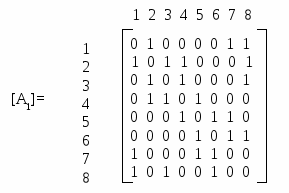
1 2 3 4 5 6 7 8

Рис.2.4.2. Два изоморфных графа и их матрицы смежности
Метод перебора

Прямым методом определения равенства матриц А1 и А2 является перестановка строк и столбцов матриц и их сравнение между собой. Для этого потребуется в общем случае n! операций, где n=|V| (для примера рис.1.4.2 потребуется 8!=40 320 операций).
Определение

Пусть имеется два графа G1 и G2, а Т1 и Т2 – таблицами инцидентности этих графов. Графы G1 и G2 будут изоморфны, если Т1 совпадает с Т2.
Алгоритм перебора

Пусть имеется два графа G1=(V1,E1) и G2=(V2,E2) со своей разметкой вершин. Каждый граф задается таблицей инцидентности.
Обозначим через v1i i-ую вершину графа G1.
Если |V1| = |V2|, то n = |V1|,
иначе графы неизоморфны.
Начальное условие: i = 1.
Сравнивая таблицы инцидентности построчно, определить совпадают ли по длине запись для v1i и записи таблицы инцидентности графа G2. Если совпадают, то изъять эти записи их обеих таблиц инцидентности, иначе графы неизоморфны.
Повторить шаг 3 для v1i, i=2,3,…,n.
После успешного выполнения алгоритма обе таблицы инцидентности будут пустыми.
Пример

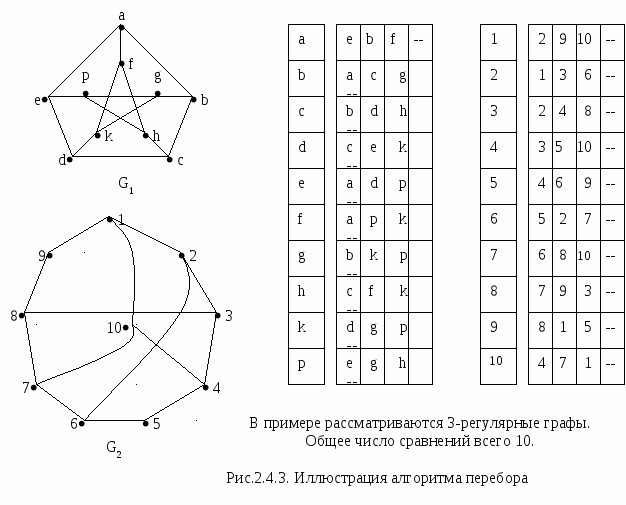
Замечание

Методы перебора в худшем случае требуют факториального времени выполнения. Существуют специальные алгоритмы перебора, выполнение которых требует значительно меньшего времени, однако они в ряде случаев все равно будут выполнены за факториальное время.
1.3.2. Каноническая матрица смежности и изоморфность графов
Определение

Код матрицы смежности А задается следующим образом:
cd= 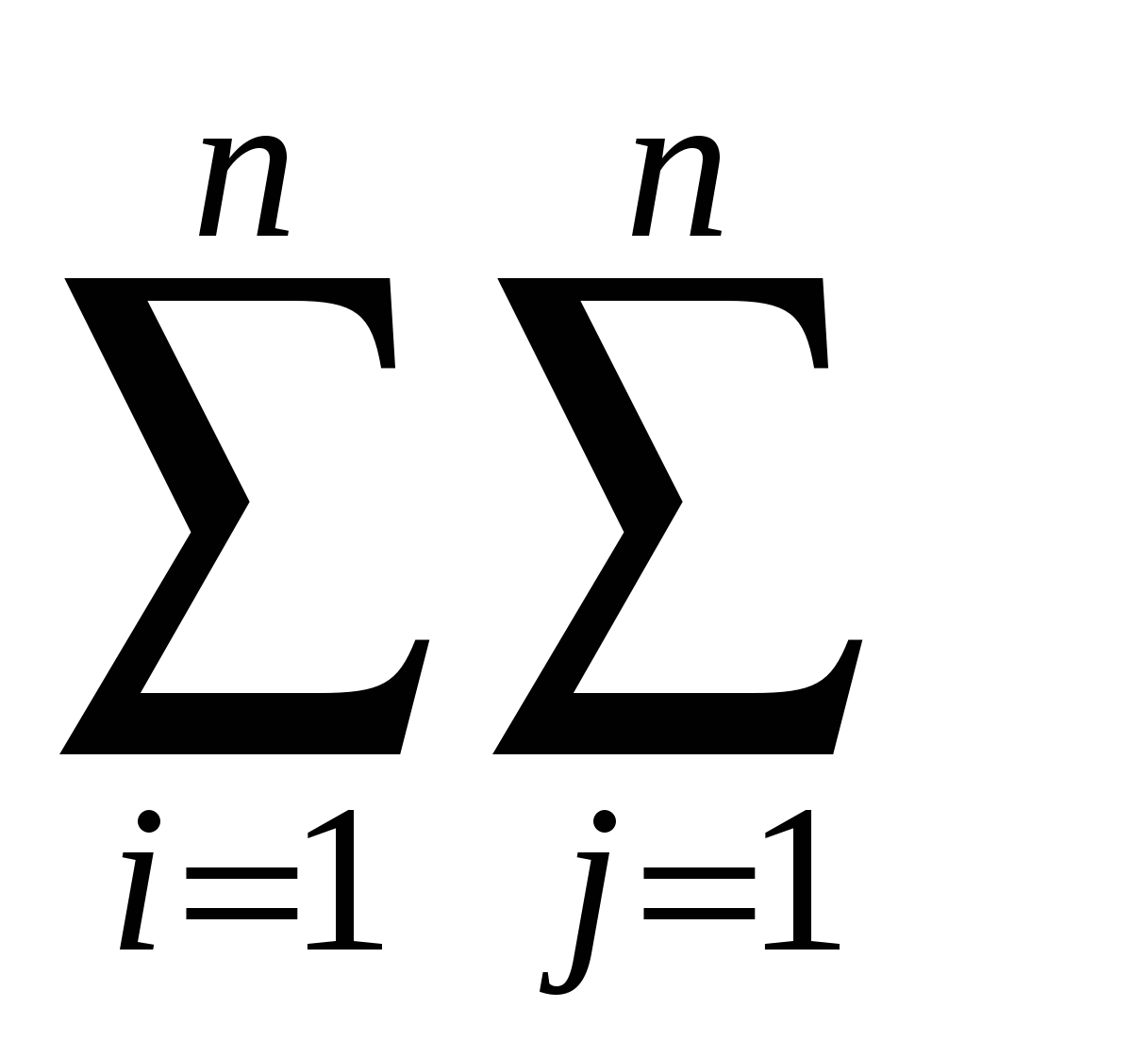 Aij 2K, Aij 2K,
где K=n2-(i-1)n-j.
В коде матрицы смежности А элементы матрицы выбираются строка за строкой в их естесственном порядке,т.е.
А11А12…А1nA21…A2n…An1…Ann .
Пример

Для матриц смежности рис.1.4.2 коды равны:
cd(A1)=262 + 257 + 256 + 255 + 253 + 252 + 246 + 244 + 240 + 238 + 237 + 235 + 228 + 226 + 225 + 219 + 217 + 215 + 211 + 210 + 27 + 25 + 22 = 4 877 487 903 930 551 460
cd(A2)= 5 021 603 092 014 697 890

М Пример ножество всех изоморфных друг другу графов образуют класс. Среди всех матриц смежности этого класса графов одна из матриц смежности будет иметь наименьший по значению код. Эта матрица называется канонической (обозначается canon(G)).

Для класса матриц рис.1.4.2 код канонической матрицы равен:
cd(canon(G)) = 507 522 663 119 374 560
Определение

Пусть G1(V,E) и G2(V,E) будут графами, а А1 и А2 – их матрицами смежности. Графы G1(V,E) и G2(V,E) будут изоморфны, если матрицы А1 и А2 сводятся к одной и той же канонической матрице.

Наиболее эффективные алгоритмы нахождения канонической матрицы смежности базируются на процедуре возврата для всех возможных перестановок имен множества вер-
шин графа.1
|
|
|
 Скачать 1.28 Mb.
Скачать 1.28 Mb.