|
|
Глава 2.Ненаправленные графы, часть 1. Простые графы (графы) Способы задания графа Основные способы задания графов графический
2.1.6. Битовые цепочки, таблицы инциденций и метод координатного хранения Определение

Для эффективного представления графа в памяти ЭВМ можно использовать представление матрицы смежности в виде битовой цепочки.
Достаточно представления только половины матрицы, т.к. вторая половина матрицы симметрична первой.
Хранение графа в памяти компьютера потребует ещё меньше места, если для графового числа использовать методы сжатия.
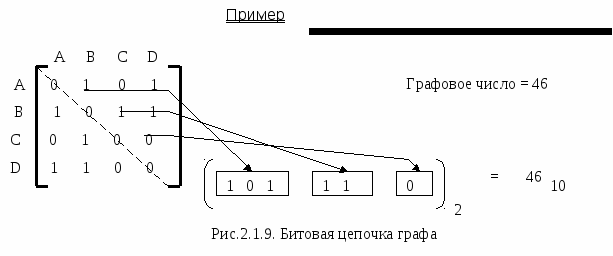
Определения

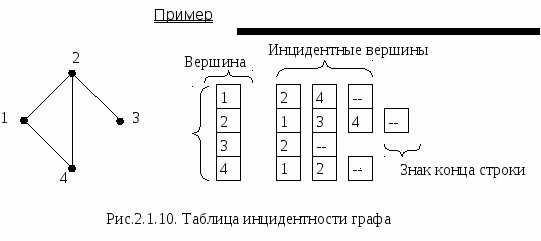
Строка таблицы инцидентности содержит вершину Vi c перечислением всех инцидентных ей вершин графа.
Данная форма записи графа особенно удобна для разреженных графов (т.е. графов с большим числом вершин и всего несколькими рёбрами).
Определения

Для разреженных матриц смежности (т.е. матриц с преобладающим числом нулей) с числом единиц NNZ используется метод координатного хранения (X-Y) матрицы в виде двух строк IROW и ICOL. В строки IROW и ICOL записываются адреса строк и столбцов матрицы связности, имеющие ненулевые элементы.

2.2. Операции над графами 2.2.1. Простейшие операции
Определения

Простейшими операциями над графами являются:
Добавление вершины: к заданному множеству вершин графа (V1, V2,…, Vn) добавляется новая вершина Vn+1, смежная с вершинами (V1, V2,…, Vn).
Добавление ребра: для заданной пары вершин v и u добавляется ребро {v,u}.
Удаление вершины: из графа вершина удаляется вместе с инцидентными ей рёбрами;
Удаление ребра: в графе удаляется ребро без инцидентных ему вершин;
Стягивание вершин: заданное множество вершин соединяется в одну, а полученные из ребер петли удаляются;
Подразбиение ребра: удаляется заданное ребро {u,v} и добавляется путь, имеющий один конец на u, а второй конец – на v.
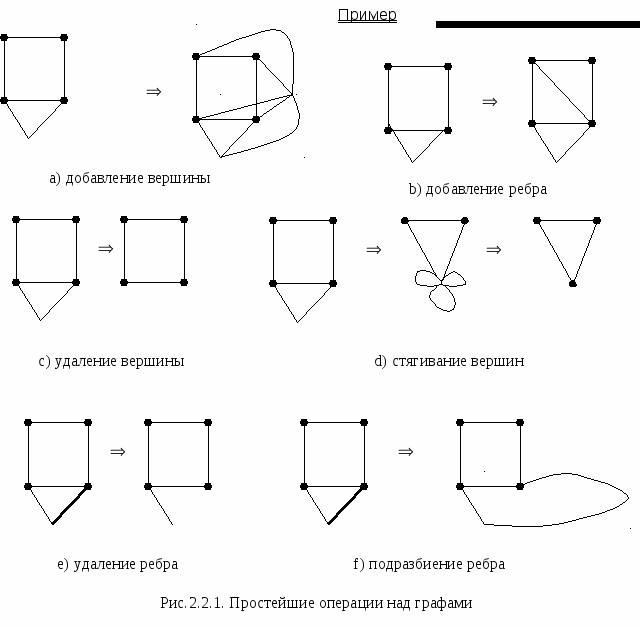
Определения

Если G(V,E)G’(V’,E’)=0, т.е. VV’=0 и EE’=0, то G и G’ являются раздельными графами.
Для раздельных графов в общем случае определены операции:
объединение раздельных графов (disjointunion) G1(V1,E1) и G2(V2,E2) –
G(V,E)= G1(V1,E1) 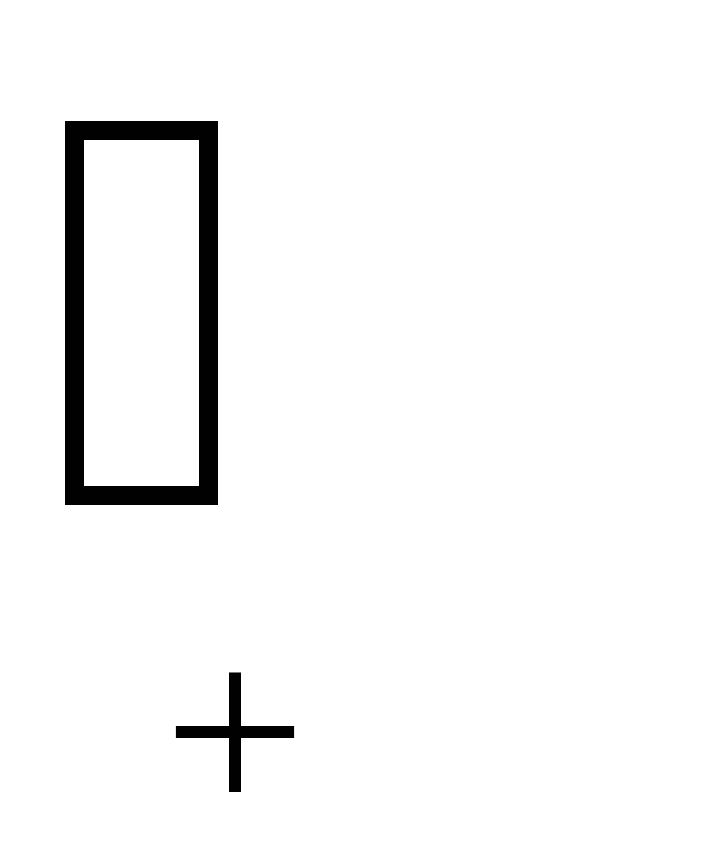 G2(V2,E2), G2(V2,E2),
если V=V1V2 и E1E2;
соединение раздельных графов (join) G1(V1,E1) и G2(V2,E2) –
G(V,E)= G1(V1,E1) 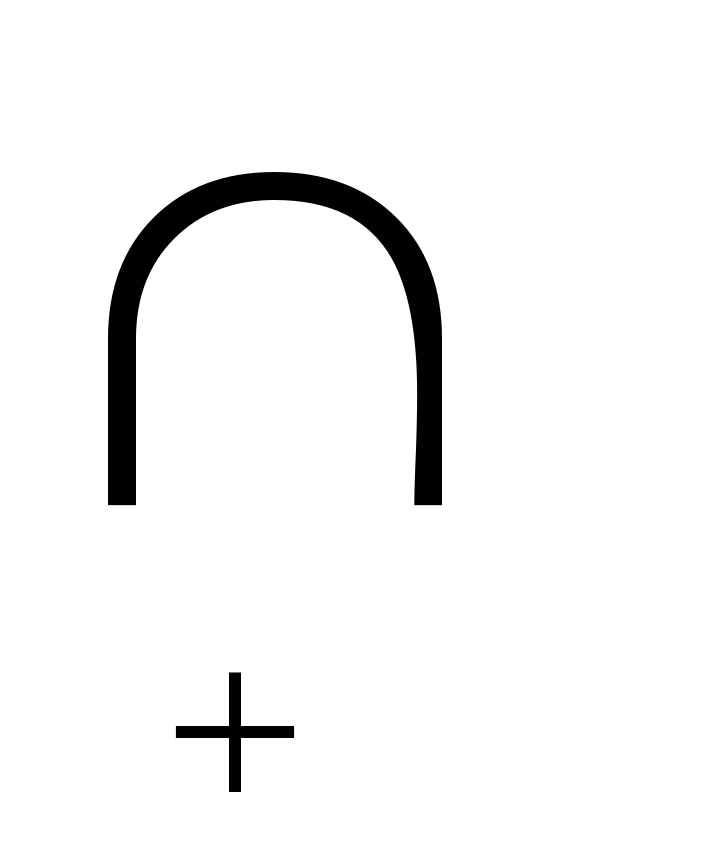 G2(V2,E2), G2(V2,E2),
где G(V,E) состоит из G1 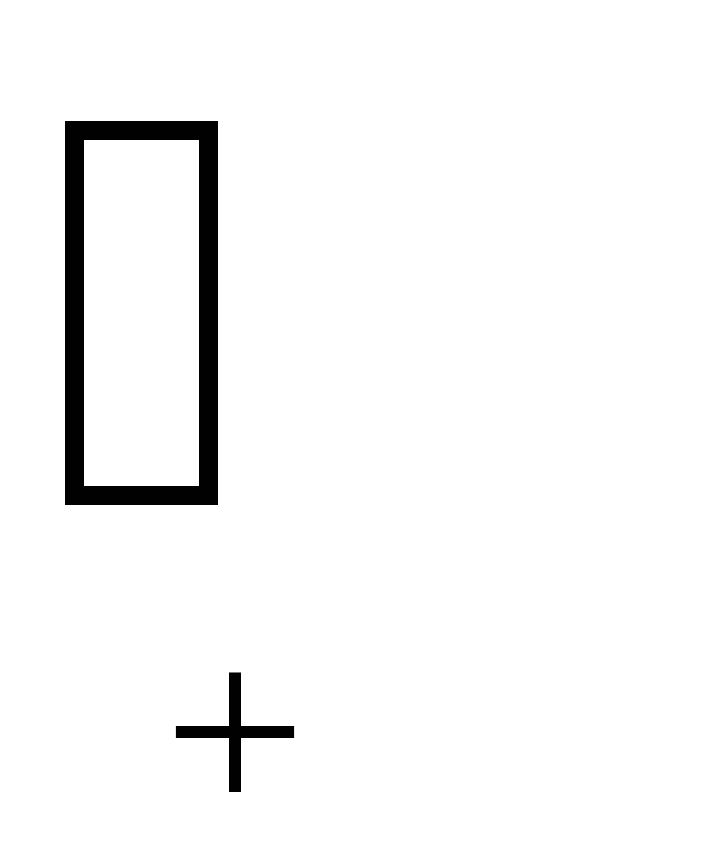 G2 G2 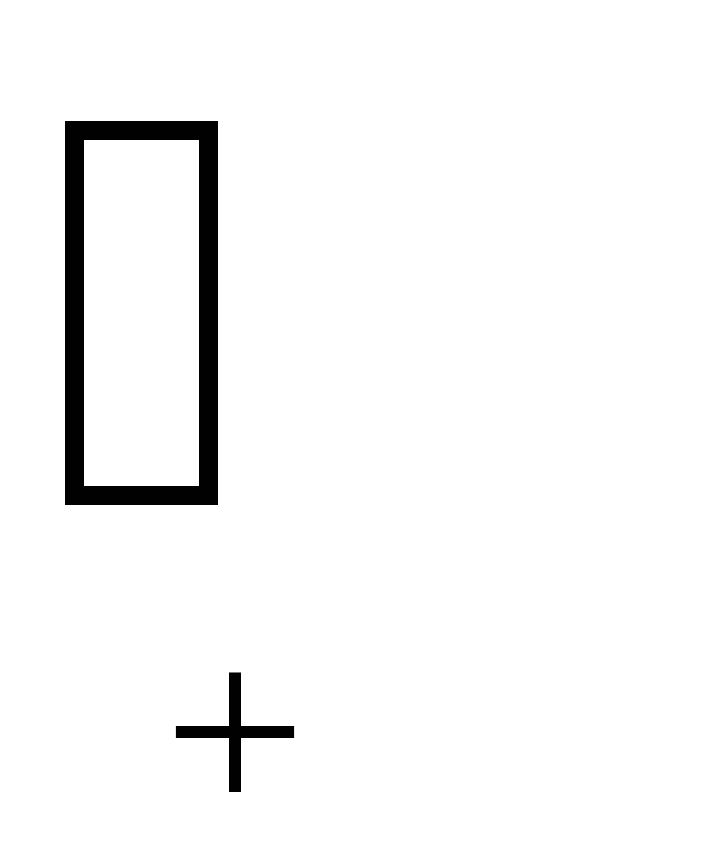 К(V1,V2); К(V1,V2);
здесь К(V1,V2) – завершенный двудольный граф с множеством вершин
V1 и V2 в долях;
произведение графов (graphproduct) G(V,E) и H(V’,E’) –
граф, у которого:
множество вершин равно V×V’ (т.е. множество пар, где первый элемент взят из множества вершин V, а второй – из множества вершин V’).
Смежность двух любых вершин произведения графов (g,h) и (g’,h’) определяется неоднозначно (всего возможно 256 различных произведений графов).
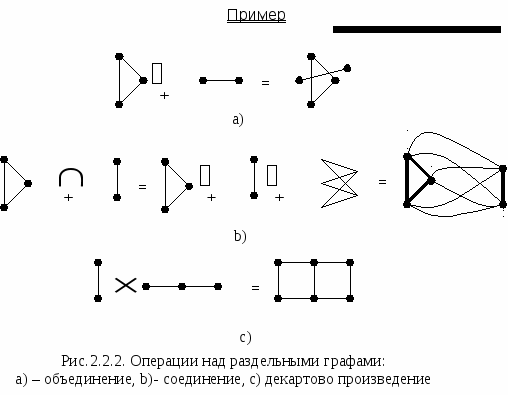
Определения

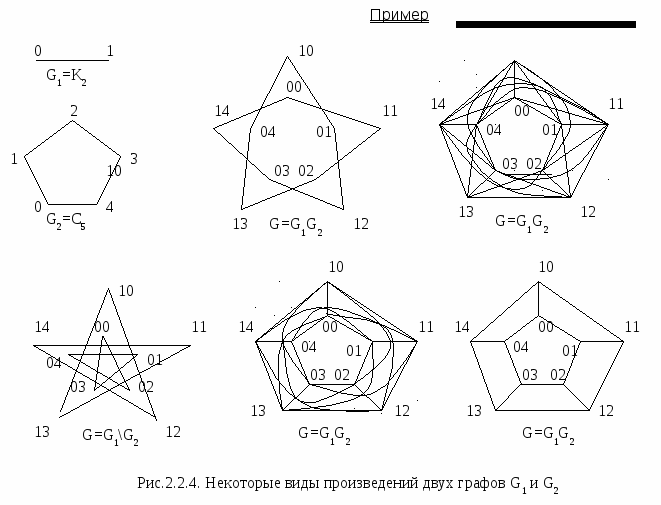
Пусть вершина произведения графов G1=(V1,E1) и G2=(V2,E2) обозначается (V1|V2) c Vi Gi (знак | обозначает операцию склеивания). Тогда некоторые из произведений двух графов определяются следующим образом: Gi (знак | обозначает операцию склеивания). Тогда некоторые из произведений двух графов определяются следующим образом:
Конъюнкция (conduction) G=G1 G2 – две вершины (U1|U2) и (V1|V2) в G соединены, если {U1,V2} есть ребро G1 и {U2,V2} есть ребро графа G2. G2 – две вершины (U1|U2) и (V1|V2) в G соединены, если {U1,V2} есть ребро G1 и {U2,V2} есть ребро графа G2.
Дизъюнкция (disjunction) G=G1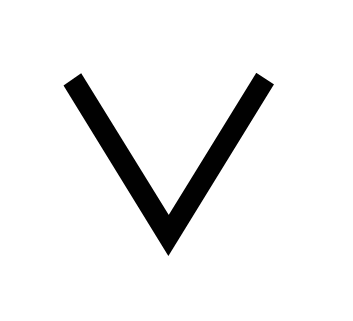 G2 – две вершины (U1|U2) и (V1|V2) соединены, если {U1,V2} есть ребро G1 или {U2,V2} есть ребро графа G2. G2 – две вершины (U1|U2) и (V1|V2) соединены, если {U1,V2} есть ребро G1 или {U2,V2} есть ребро графа G2.
Симметричная разница (symmetric difference) G=G1 G2 - две вершины (U1|U2) и(V1|V2) соединены, если {U1,V2} есть ребро G1, либо {U2,V2} есть ребро графа G2 (но не оба сразу). G2 - две вершины (U1|U2) и(V1|V2) соединены, если {U1,V2} есть ребро G1, либо {U2,V2} есть ребро графа G2 (но не оба сразу).
Отклонение (rejection) G=G1\G2 - две вершины (U1|U2) и(V1|V2) соединены, если ни {U1,V2} не является ребром G1, ни {U2,V2} не является ребром графа G2.
Декартово произведение (Cartesian product) G=G1 G2 - две вершины (U1|U2) и(V1|V2) соединены, либо U1 и V1 идентичны и {U2,V2} есть ребро G2, либо U2 и V2 идентичны и {U1,V1 } есть ребро графа G1. G2 - две вершины (U1|U2) и(V1|V2) соединены, либо U1 и V1 идентичны и {U2,V2} есть ребро G2, либо U2 и V2 идентичны и {U1,V1 } есть ребро графа G1.
Замечание

Вычисление произведения двух графов обычно весьма трудоемкая задача.
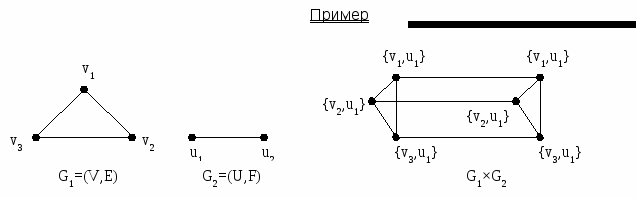
Вершины: {v1,u1},{v1,u2},{v2,u1},{v2,u2},{v3,u1},{v3,u2}
Ребра (заданы в виде пары вершин):


Декартово произведение графов позволяет просто вычислить некоторые структурные свойства произведения по свойствам сомножителей.
Например, если G1 и G2 – графы и X={ x1, x2 } и Y={y1,y2} – две вершины в G1 G2, то: G2, то:
| G1 G2|=|G1| . |G2| G2|=|G1| . |G2|
где |G| - порядок графа,
. -операция арифметического умножения.
deg G1 G2 (X)= degG1(x1) + degG2(x2), G2 (X)= degG1(x1) + degG2(x2),
где degG(V) – степень вершины V графа G.
D G1 G2 = DG1+ DG2, G2 = DG1+ DG2,
где DG – диаметр графа G.
dist G1 G2(X,Y) = distG1(x1, y1) + distG2(x2,y2), G2(X,Y) = distG1(x1, y1) + distG2(x2,y2),
где dist G(X,Y) – длина кратчайшего пути между вершинами X и
Y графа G.
|
|
|
 Скачать 1.28 Mb.
Скачать 1.28 Mb.