Глава 2.Ненаправленные графы, часть 1. Простые графы (графы) Способы задания графа Основные способы задания графов графический

• Название: Простые графы (графы) Способы задания графа Основные способы задания графов графический
• Анкор: Глава 2.Ненаправленные графы, часть 1.doc
• Дата: 04.09.2018
• Размер: 1.28 Mb.
• Имя файла: Глава 2.Ненаправленные графы, часть 1.doc
• Тип: Глава; #24055
• страница: 1 из 14

Глава 2.

ПРОСТЫЕ ГРАФЫ (ГРАФЫ)

2.1. Способы задания графа

Основные способы задания графов:

• 
  графический;
  
• 
  с помощью множеств;
  
• 
  последовательность степеней графа;
  
• 
  матричный;
  
• 
  битовые цепочки и таблицы инцидентности.
  

2.1.1. Графический способ задания графа

Определения

На плоскости (в пространстве или на объемной фигуре) изображается некоторое количество точек (кружков) и какое-то число отрезков, кривых или ломаных линий соединяющих все, или некоторые из точек.

Кружки называются вершинами, а линии – ребрами, а полученная геометрическая фигура – ненаправленным графом (графом).

Замечание

Ребра показывают лишь связь между двумя вершинами, или ее отсутствие, однако направление этой связи (например, передача инфор­мации, сигналов, товаров, топлива, грузов и т.д.) в данной модели несущественно. Вот по­чему такие графы называются ненаправленными.



Ребро, соединяющее вершину саму с собой, называется петлей.

Несколько ребер, соединяющих две вершины, носят название кратных.

В зависимости от наличия или отсутствия петель и/или кратных ребер различают следующие типы ненаправленных графов:

Тип	Наличие кратных ребер	Наличие петель
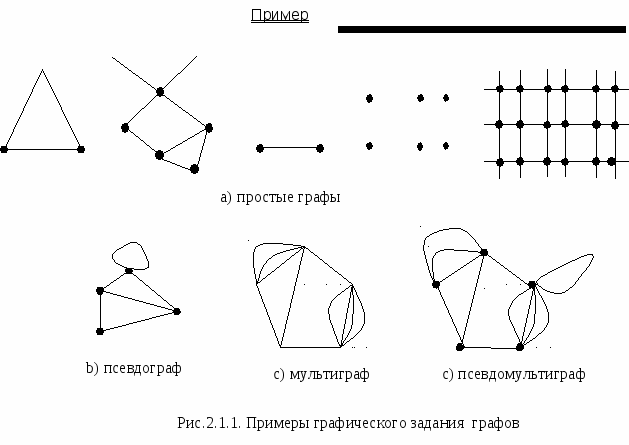
Простой граф Мультиграф Псевдограф Псевдомультиграф	Нет Да Нет Да	Нет Нет Да Да

Замечание

Далее будут рассматривать простые графы, которые будут кратко называться графами.

2

Определения

.1.2 Определение графа с помощью множеств

Множество называется поименованным, если каждому его элементу присвоено имя (метка, целое число).

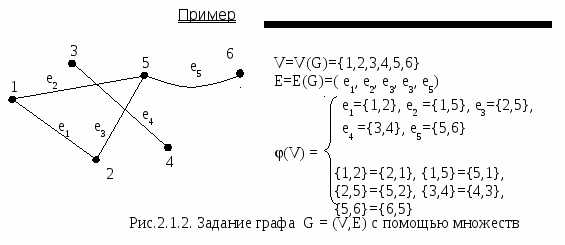
В дальнейшем графом будет называться пара разделенных поименованных множеств G = (V,E) (V∩E = ) и функция преобразования : (V)  Е.

Элементы множества V=V(G) являются вершинами графа G, а элементы множества E=E(G) – его ребрами. Функция преобразования устанавливает соответствие между именами ребер и неупорядоченными парами имен вершин. Поэтому ребра можно задавать как собственными именами, так и неупорядоченными парами имен вершин.

В дальнейшем для краткости записи функция преобразование  будет опускаться.

Определения

Граф G=(V,E) называется пустым, если |V(G)|≠0 , |E(G)|=0.

Нулевой граф – это граф G=(V,E) с |V(G)|=0 и |E(G)|=0.

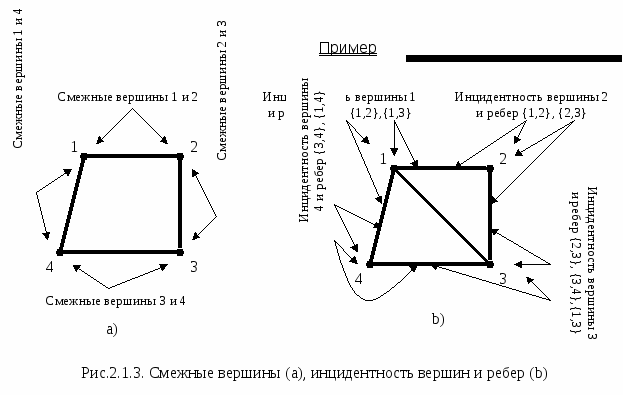
Две вершины V_i и V_k называются смежными, если существует ребро, соединяющее эти вершины.

Ребра являются смежными, если они опираются на общую вершину.

Вершина графа v и некоторое его ребро е называются инцидентными, если e={v,w} или e={w,v}, где w – некоторая вершина графа.

Вершина будет изолированной, если она не инцидентна ни с одним ребром.

Меры

• 
  Порядок графа |G| - число вершин графа, |G|=|V|.
  
• 
  Размер графа ||G|| - число ребер графа, ||G||=|E|.
  

2.1.3. Степени вершин графа

Определения

Степенью вершины графа V_iV(G) (записывается как deg(V_i)) является число рёбер, смежных с вершиной V_i.

Изолированная вершина имеет deg(V_i)=0.

Очевидно, поскольку степень вершин задаёт число смежных вершин, deg(V_i)>0 для всех неизолированных вершин V_iV(G). Если граф G имеет n вершин, то каждая вершина в графе максимально может иметь рёбра с другими n-1 вершинами (кроме ребра с самой собой, т.е. петли). Поэтому deg(V_i)n-l. От­сюда следует оценка для любого простого графа:
0 deg (V_i)  n-1

Меры

• 
  Степень вершины deg(V_i).
  
• 
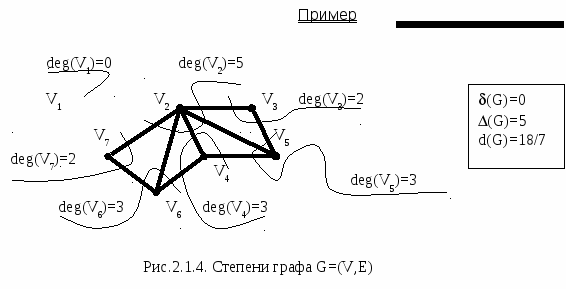
  Минимальная степень графа δ(G)= min{deg(Vi) | V_iV}.
  
• 
  Максимальная степень графа Δ(G)= max{deg(Vi) | V_iV}.
  
• 
  Средняя степень графа
  

d(G) =

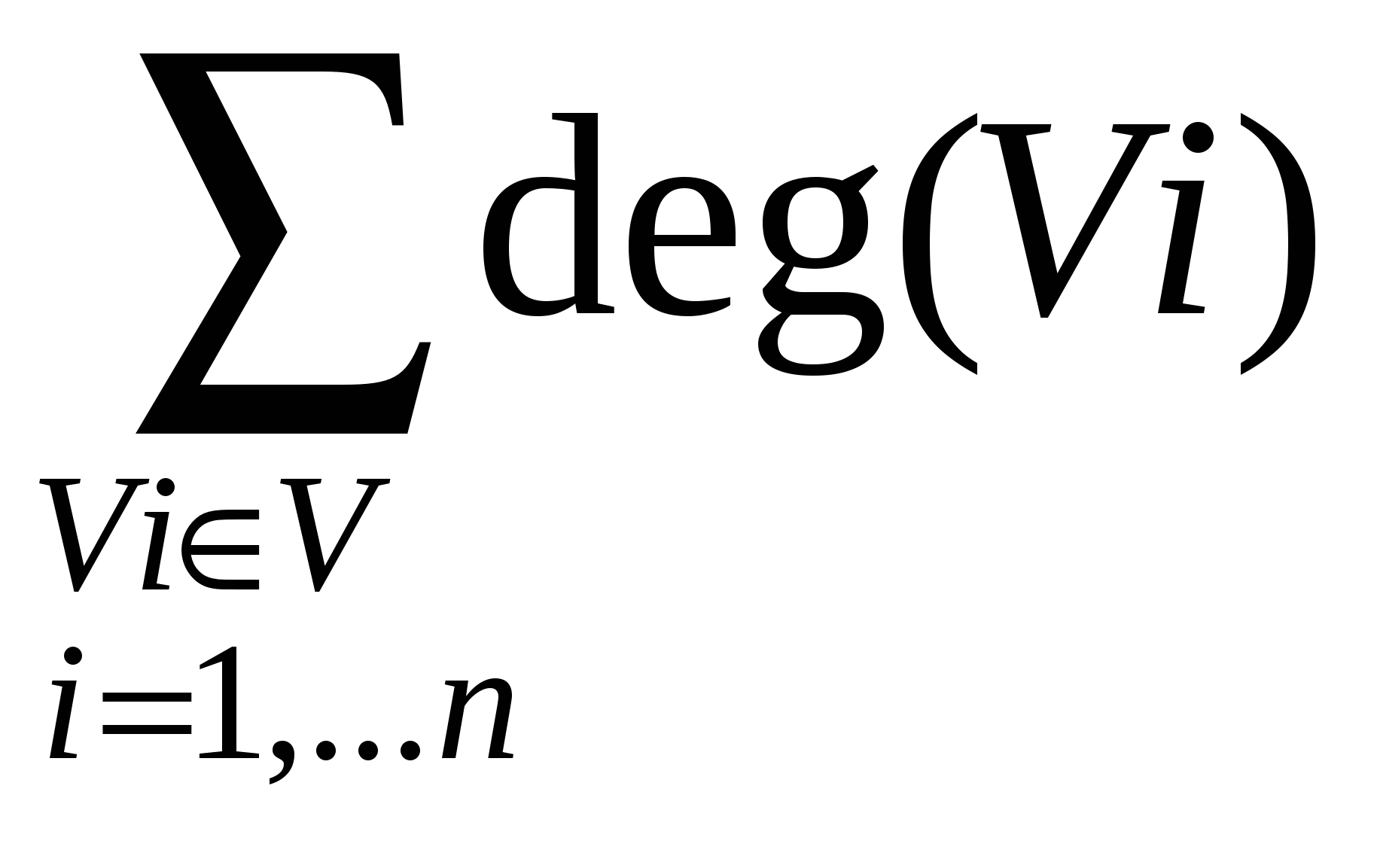
Лемма о рукопожатиях

Пусть G=(V,E) будет графом. Тогда

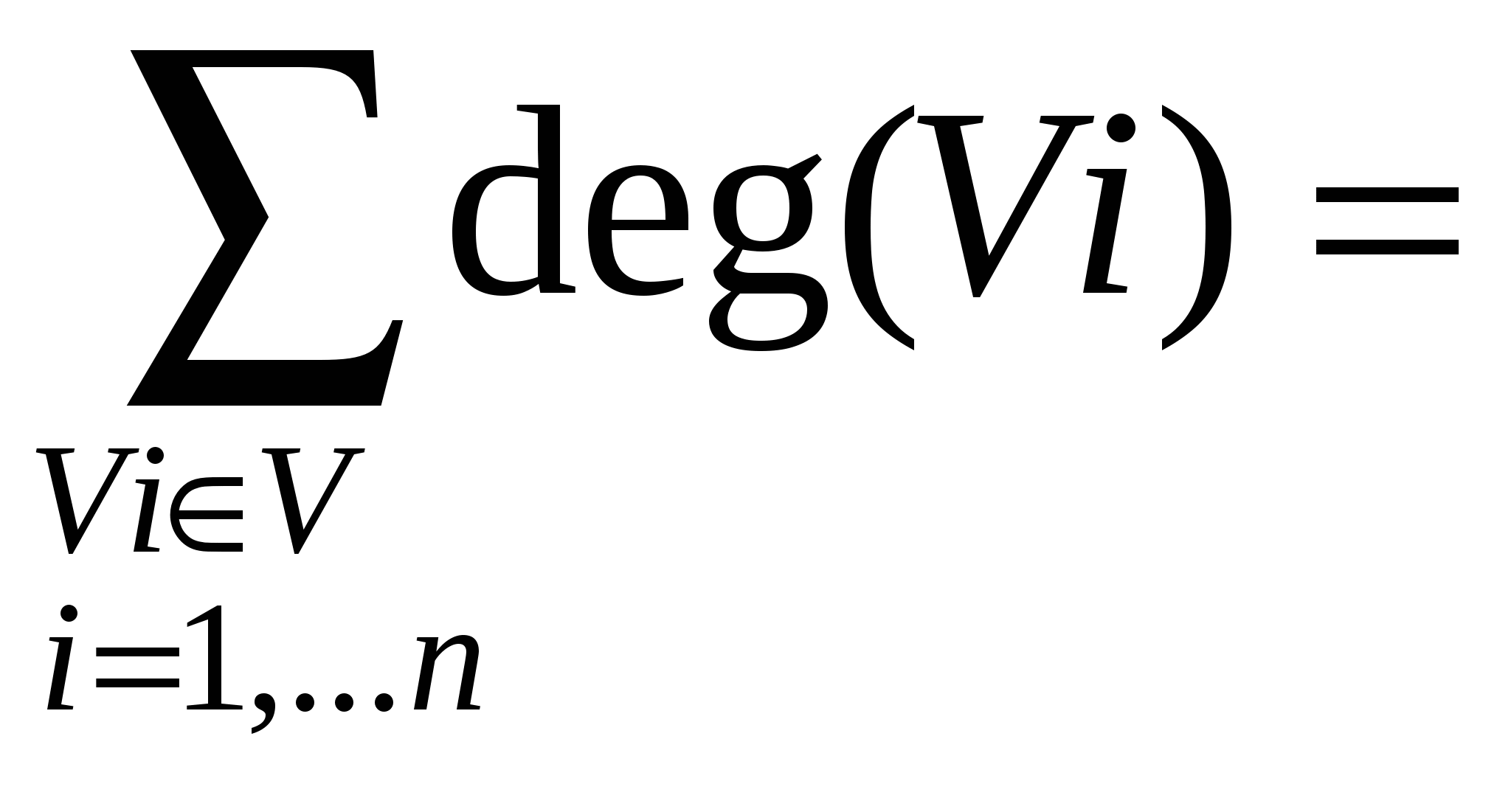2E

Данное утверждение легко получить, если отметить, что в сумму степеней каждое реб­ро вносит 2 подсуммы: одну для вершины V_i, а вторую - для вершины V_j

Важно подчеркнуть, что лемма говорит о том, что степень всех вершин графа всегда четна.