|
Глава 2.Ненаправленные графы, часть 1. Простые графы (графы) Способы задания графа Основные способы задания графов графический
2 Определения .3.3. Инварианты

Пусть f- функция, относящая каждому графу G некоторый элемент f(G) из множества М произвольной природы.
Эта функция показывается инвариантом, если на изоморфных графах её значение совпадают, т.е. для любых G и G’ из изоморфизма графов G и G’ следует f(G)=f(G’).
Инвариант должен легко вычисляться по заданному графу (и по возможности иметь наглядный смысл) и обладать свойством полноты, т.е. определяя граф однозначно с точностью до изоморфизма.
Во многих случаях инварианты имеют всего два значения, 0 и 1 . Значение 1 показывает, что это свойство у графа имеется, а 0 – что это свойство отсутствует. К таким инвариантам относятся:
связность,
планарность,
является ли граф деревом,
является ли граф двудольным
и т.д.
Другую группу составляют инварианты, равные натуральным числам:
число вершин и рёбер;
степень вершин;
последовательность степеней вершин;
число компонент связности;
хроматическое число;
наличие пути заданной длины;
наличие гамильтонова цикла;
число связных компонент
и т.д.
К сожалению, нет универсального алгоритма определения изоморфизма для всех графов по одному инварианту.
Определения
Система инвариантов называется полной системой инвариантов, если из того, что для некоторых двух графов эти инварианты принимают одинаковые значения, следует, что данные графы изоморфны.
Системы инвариантов существуют, но их нахождение является сложнейшей задачей.
2.5. Прогулки, тропы, пути и циклы
Определения

Прогулкой (wаlk) (или [V0-Vm]-прогулкой) в графе G=(V,E) называется последовательность чередующихся вершин и рёбер (V0 , e1, V1, e2, V2, e3, V3… em , Vm), в которой еi = { Vi-1 , Vi } для 1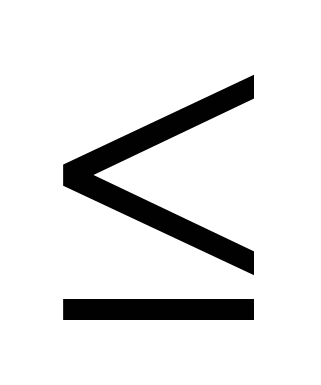 i i 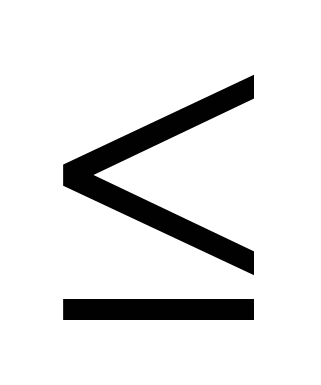 k . k .
Для прогулки нет требования отсутствия повторения вершин и /или ребер. Однако если ввести это требование, то получим особые определения:
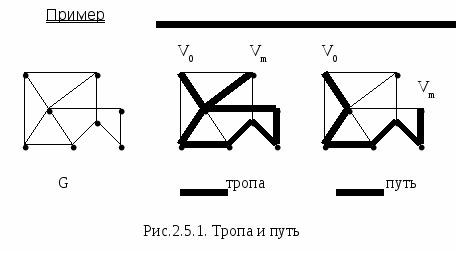
Тропа (trail) – это прогулка, в которой запрещены повторы рёбер.
Путь (path) – это прогулка, в которой запрещены повторы вершин.
Из выше приведённых определений можно сделать следующие выводы:
каждый путь есть тропа, и каждая тропа есть прогулка;
имеются прогулки, которые не будут тропами, и тропы, которые не будут путями.
Прогулка или тропа будут замкнутыми, если они их концевые вершины совпадают.
Пусть x и y будут вершинами графа G. Тогда можно говорить о (x-y)-прогулке, (x-y)-тропе или (x-y)-пути, которые имеют концевые вершины x и y.
Теорема

Если граф G имеет (x-y)-прогулку, то он имеет (x-y)-путь.
Меры

длина прогулки (тропы или пути) d(u,v) – число ребер, входящих в прогулку
(тропу, путь) с начальной вершиной u и конечной вершиной v.
расстояние dist(u,v) между двумя вершинами u и v. Определяется как длина
минимального пути между этими вершинами.
Класс сложности

Нахождение минимального (кратчайшего) пути между двумя вершинами простого графа требует линейного времени.
Алгоритм

Найти кратчайшие пути от заданной вершины до всех вершин связного графа можно, исполнив алгоритм обхода в ширину (BFS).
Теорема
Пусть G=(V,E) будет графом с n вершинами v1 ,v2, …, vn и матрицей смежности А. Тогда для любого положительного целого числа m (i,j)-элемент матрицы смежности Аm (m – степень матрицы) будет равен числу прогулок длины m из вершины vi в вершину vj , i,j = 1,2,…,n.
Меры

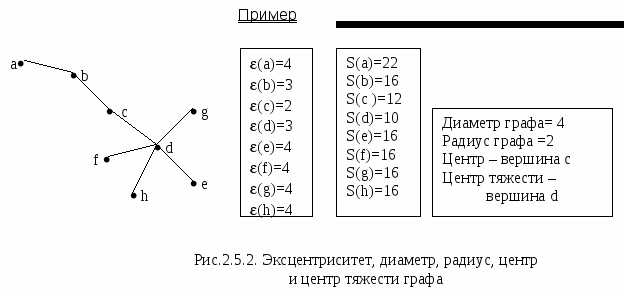
Эксцентриситет (u) вершины u - максимальный из всех путей от этой вершины до всех остальных вершин графа.
Диаметр DG - максимальный эксцентриситет графа.
Радиус RG - минимальный эксцентриситет графа.
Сумма расстояний вершины S(u) - сумма расстояний от этой вершины до всех остальных вершин графа
Центр тяжести графа - вершина с минимальной суммой расстояний
Замечания

Вершины графа, эксцентриситет которых равен радиусу, образуют центр графа, а вершины с эксцентриситетом, равным диаметру, находятся на периферии графа.
Центр и центр тяжести графа не всегда совпадают.
Класс сложности

Проблема нахождения максимального пути в графе относится к NP-тяжелым.
Определения

Замкнутой прогулкой будет прогулка, которая начинается и заканчивается на одной и той же вершине. Подобным образом определяется замкнутая тропа – тропа, которая начинается и заканчивается на одной и той же вершине.
Для простого графа циклом называется замкнутая прогулка длины не менее трех, т.е. у цикла все вершины различны, кроме первой и последней.
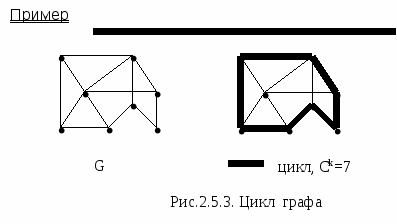

Ck – длина цикла - равна числу входящих в цикл k ребер.
g(G) – обхват графа – цикл минимальной длины, содержащийся в G.
С(G) – окружность графа - цикл максимальной длины, содержащийся в графе G.
Пример

g(G)=1  граф содержит одну или более петель (является псевдографом) граф содержит одну или более петель (является псевдографом)
g(G)=2  граф содержит кратные ребра, но не содержит петель (мультиграф) граф содержит кратные ребра, но не содержит петель (мультиграф)
g(G) 3 3  G является простым графом G является простым графом
g(G)=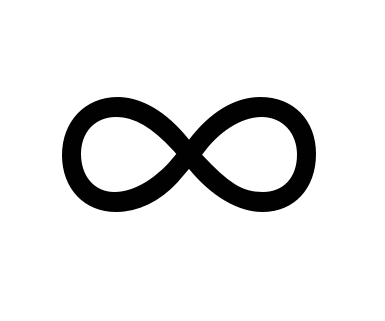  G не содержит циклов G не содержит циклов
Теоремы

Теорема 1

Если граф G имеет минимальную степень δ(G)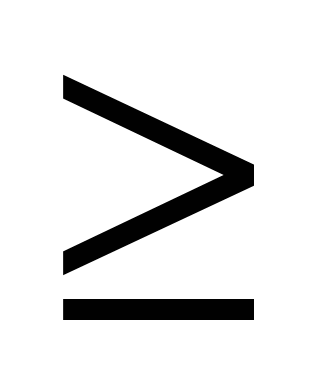 2, то этот граф содержит цикл. 2, то этот граф содержит цикл.
Теорема 2

Каждая замкнутая с нечетной длиной прогулка графа содержит цикл нечетной длины.
Теорема 2

Каждый граф, имеющий четные степени вершин, операцией декомпозиции может быть разбит на циклы.
Класс сложности

Нахождение циклов в графе требует линейного времени.
Алгоритмы

Найти простые циклы в связном графе можно с помощью алгоритма обхода графа в глубину (DSF).
Циклы связного графа могут быть найдены линейной комбинацией фундаментальных циклов.
|
|
|
 Скачать 1.28 Mb.
Скачать 1.28 Mb.