Методичка по работе в MS Excel (статистические методы). Рабочая программа дисциплины Статистические расчеты в ms excel

• Название: Рабочая программа дисциплины Статистические расчеты в ms excel
• Анкор: Методичка по работе в MS Excel (статистические методы).doc
• Дата: 30.01.2017
• Размер: 6.25 Mb.
• Имя файла: Методичка по работе в MS Excel (статистические методы).doc
• Тип: Рабочая программа; #1241
• Категория: Медицина
• страница: 6 из 9

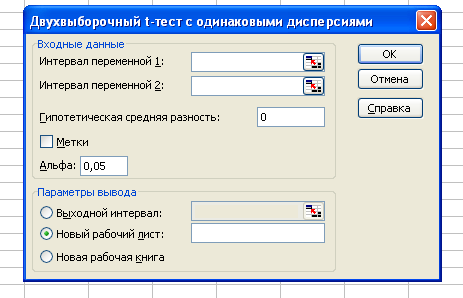
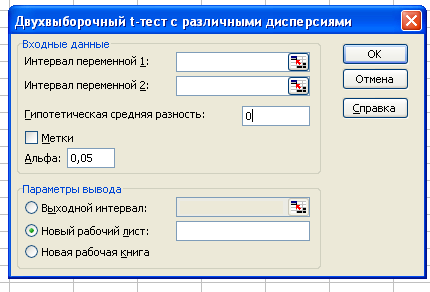
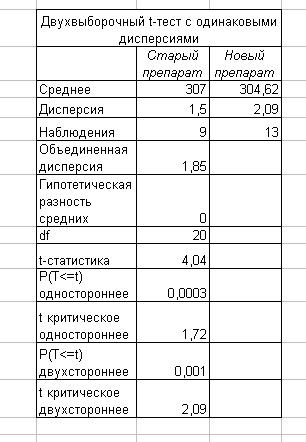
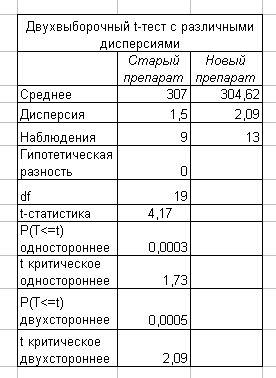
4. Методы проверки статистических гипотез

4.1. Понятие статистической гипотезы

Проверка статистических гипотез является одним из самых важных статистических методов, применяемых в медицинских исследованиях.

Под статистической гипотезой понимают всякое высказывание о генеральной совокупности (случайной величине), проверяемое по выборке (по результатам наблюдений). Процедуру сопоставления высказанной гипотезы с выборочными данными называют проверкой статистической гипотезы.

Проверяемую статистическую гипотезу принято называть основной (или нулевой) гипотезой (обозначается H₀), а противоречащую ей гипотезу - альтернативной (или конкурирующей) гипотезой (обозначается Н₁). Нулевая гипотеза обычно заключается в том, что изучаемое вмешательство не оказывает значимого воздействия на генеральные параметры распределения, и альтернативная, исследовательская гипотеза. Изначально предполагается, что вмешательство не влияет. Любые различия между изучаемыми группами объясняются случайностью, и становится задача опровергнуть это предположение

Поскольку при проверке статистических гипотез приходится иметь дело со статистическим материалом, то, отвергая или принимая нулевую гипотезу, всегда рискуем совершить ошибку. Ошибку, заключающуюся в том, что нулевая гипотеза отвергается, тогда как она в действительности верна, называют ошибкой первого рода. Ошибку, состоящую в том, что нулевая гипотеза не отвергается, тогда как она в действительности неверна, называют ошибкой второго рода.

Проверка статистических гипотез осуществляется с помощью различных статистических критериев. В качестве критерия используется некоторая случайная величина, значения которой могут быть вычислены на основе имеющихся данных. В множестве возможных значений критерия выбирается подмножество, называемое критической областью. Если вычисленное значение критерия принадлежит критической области, то нулевая гипотеза отвергается.

Критическая область выбирается таким образом, чтобы вероятность совершить ошибку первого рода не превосходила некоторого заранее определенного положительного числа α. Это число α называют уровнем значимости и говорят: «нулевая гипотеза отвергается на уровне значимости α. В качестве α обычно берут одно из чисел: 0,05; 0,01; 0,001.

Вероятность совершить ошибку второго рода обозначается β. Величина 1-β называется мощностью критерия; она равна вероятности отвергнуть неверную гипотезу Чаще всего множество возможных значений критерия принадлежит некоторому интервалу. Интервалом является и критическая область. Граничные точки критической области называются критическими точками. Критические точки выбираются таким образом, чтобы при выбранном уровне значимости, а мощность критерия (1 - β) была наибольшей.

4.2. Двухвыборочный t-тест для средних. Технология работы

Часто в медицинских исследованиях требуется оценить достоверность различий между двумя выборками. Это могут быть выборки из разных совокупностей (например, сравнение опытной и контрольной групп), а также выборки из одной совокупности (например, исследование какого-либо параметра в одной выборке до и после проведения эксперимента).

Двухвыборочный t-тест проверяет равенство средних значений генеральной совокупности по каждой выборке. Расчет проводится по формуле: В пакете статистического анализа Excel реализовано три варианта использования t-теста: равные дисперсии генерального распределения, дисперсии генеральной совокупности не равны, а также представление двух выборок до и после наблюдения по одному и тому же субъекту.

Режимы работы «Двухвыборочный t-тест с одинаковыми дисперсиями» и «Двухвыборочный t-тест с различными дисперсиями» служат для проверки гипотез о различии между средними (математическими ожиданиями) двух нормальных распределений соответственно с неизвестными, но равными дисперсиями () и с неизвестными дисперсиями, равенство которых не предполагается.

Параметры, задаваемые для расчетов, отображены на рисунке 17.

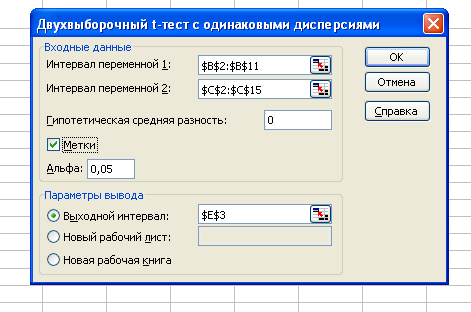
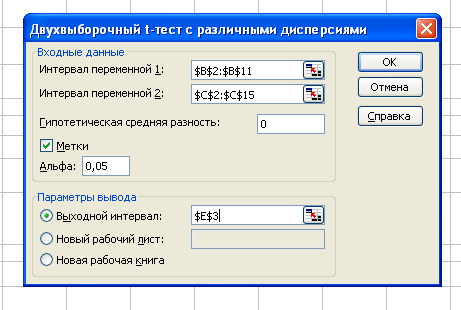
Рис. 17

Пример. На рабочем листе Microsoft Excel сформирована таблица, отражающая расход в граммах (на 100 м² площади) на дезинфекцию отделений с использованием старого и нового дезинфицирующего препарата (рис. 18).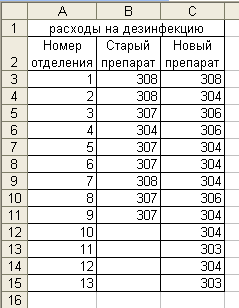


Рис. 18
При уровне значимости α = 0,05 требуется проверить гипотезу H₀: а_х= а_у, предположив, что соответствующие генеральные совокупности X и Y имеют нормальные распределения: 1) с одинаковыми дисперсиями и ; 2) с различными дисперсиями и .

Для проверки предположения 1 используем режим работы «Двухвыборочный t-тест с одинаковыми дисперсиями», а для проверки предположения 2 - «Двухвыборочный t-тест с различными дисперсиями». Значения параметров, установленных в одноименных диалоговых окнах, представлены на рис. 19, а рассчитанные в этих режимах показатели — в табл. 20 соответственно.

Рис. 19

Рис. 20

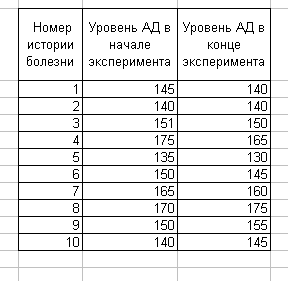
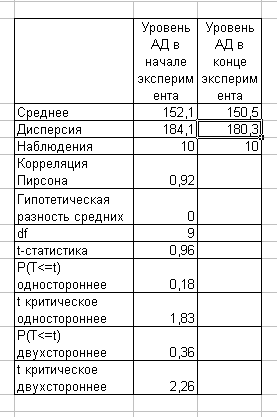
Так как и в первом, и во втором варианте расчета показатели t-статистики = 4,04 и 4,17 соответственно превышали t - критическое = 2,09 то гипотезу H₀: а_х=а_у отвергаем, т. е. при переходе на новый дезинфицирующий препарат происходит уменьшение его среднего расхода на обработку 100 м².

Рассмотренные выше процедуры сравнения двух выборок часто применяются для обнаружения результата какого-либо воздействия либо, напротив, для подтверждения его отсутствия. Чем более однородными окажутся выбранные для эксперимента объекты (для контроля и воздействия), чем меньше их случайные различия, тем точнее можно будет дать ответ на поставленный вопрос. Ясно, что различие между объектами, выбранными для воздействия и для контроля (или для двух разных воздействий, если интерес представляет их сопоставление), будет наименьшим, если в обоих качествах выступает один и тот же объект.

Если это возможно, то далее обычным порядком составляется группа экспериментальных объектов и затем для каждого объекта измеряются два значения интересующей нас характеристики (например, до воздействия и после или при двух разных воздействиях). Так возникают пары наблюдений или парные данные.

Пусть x_i и y_i — результаты измерений для объекта номер i, i= 1, ..., n, где n - численность экспериментальной группы (число объектов). Тогда совокупность пар случайных величин (x₁, y₁)..., (x_n … у_n) образует парные данные. Как обычно, все наблюдения будем считать реализациями случайных величин и предполагать, что методика эксперимента обеспечивает их независимость для разных объектов. Но наблюдения, входящие в одну пару, нельзя считать независимыми, поскольку они относятся к одному и тому же объекту. Эти два наблюдения отражают свойства общего для них индивидуального объекта и потому могут зависеть друг от друга. Для пар наблюдений (x₁, y₁) введем величину z_i =у,- x₁, которую будем считать независимой и нормально распределенной. Тем самым задача о парных данных сводится к задаче об одной нормальной выборке при неизвестной дисперсии.

Режим работы «Парный двухвыборочный t-тест для средних» служит для проверки гипотезы о различии между средними (математическими ожиданиями) двух нормальных распределений на основе парных выборочных данных. При этом равенство дисперсий генеральных совокупностей не предполагается (≠ ). В диалоговом окне данного режима задаются параметры, аналогичные параметрам, задаваемым выше.

Пример. Проводили клинический эксперимент. Измеряли артериальное давление у группы пациентов в начале лечения препаратом и в конце. Исходные данные и результаты расчетов приведены в таблице, сформированной в MS Excel (рис. 21). Требовалось проверить, повлиял ли препарат на уровень артериального давления.

Рис. 21

Как видно из результатов расчета показатель t-статистики =0,96 превышал t - критическое = 2,26, поэтому гипотезу H₀:а_х=а_у принимаем, т. е. действие препарата не привело к уменьшению средних параметров давления.