Методичка по работе в MS Excel (статистические методы). Рабочая программа дисциплины Статистические расчеты в ms excel
 Скачать 6.25 Mb.
|
5.3. Регрессия. Краткие сведения из теории статистикиВ практике статистического исследования весьма часто возникает необходимость определить не только корреляционное соотношение между изучаемыми характеристиками, но и установить определенную обусловленность между ними, представив выявленную связь в строгой аналитической форме. В этом случае результат исследования – экспериментальная зависимость воздействия какого-либо фактора (скажем, производительности труда, уровня образования, практического стажа работы и т.д.) на изменение изучаемого параметра (например, величины прибыли фирмы) − может быть не только представлен в виде графика (что весьма наглядно), но и описан математически с использованием аппроксимирующего выражения (эмпирической формулы). Исследование такой ситуации и является задачей регрессионного анализа, который дает предсказание (прогнозирование) одной переменной на основании другой. Регрессионный анализ четко распределяет роли между изучаемыми характеристиками − одна из них является аргументом, а вторая функцией. Переменная, которая прогнозируется (функция), обозначается как у, а переменная, которая используется для такого прогнозирования (аргумент или фактор), − это х. Таким образом, в случае выявления корреляции дается попытка ответить на вопрос: «Существует ли связь?» Целью регрессионного анализа является поиск ответа на уже более сложный вопрос: «Каков вид этой связи? Что на что влияет?» Однако в последнем случае речь не идет о выяснении механизма причинности обнаруженной связи, т.е. не ставится вопрос «Почему существует связь?» Это уже считается проблемой специального исследования, касающегося выявления физической (или социальной) природы изучаемого процесса. Форма связи результативного признака Y с факторами X1, X2, …Xm получила название уравнения регрессии. В зависимости от типа выбранного уравнения различают линейную и нелинейную регрессию (в последнем случае возможно дальнейшее уточнение: квадратичная, экспоненциальная, логарифмическая и т. д.). В зависимости от числа взаимосвязанных признаков различают парную и множественную регрессию» Если исследуется связь между двумя признаками (результативным и факторным), то регрессия называется парной, если между тремя и более признаками - множественной (многофакторной) регрессией. При изучении регрессии следует придерживаться определенной последовательности этапов: 1. Задание аналитической формы уравнения регрессии и определение параметров регрессии. 2. Определение в регрессии степени стохастической взаимосвязи результативного признака и факторов, проверка общего качества уравнения регрессии. 3. Проверка статистической значимости каждого коэффициента уравнения регрессии и определение их доверительных интервалов. Основное содержание выделенных этапов рассмотрим на примере множественной линейной регрессии, реализованной в режиме «Регрессия» надстройки Пакет анализа Microsoft Excel. 5.4. Расчет параметров уравнение регрессии. Технология работы Для расчета параметров уравнения регрессии воспользуемся следующим примером. В аптеке продается новый препарат для профилактики гриппа. Необходимо выяснить как объем продаж y (число упаковок в день) зависит от а) числа покупателей, которые слышали рекламу этого препарата (их доля от общего числа покупателей x1, %) и работе в торговом зале врача-консультанта (относительное время x2, когда он работал, %). Исходные данные представлены в таблице. Таблица 2
Разместим исходные данные на лист табличного редактора в следующем виде (рис. 25). 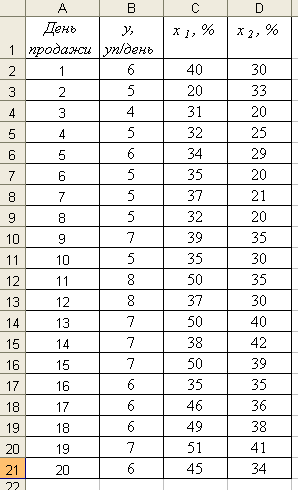 Рис. 25 Режим работы «Регрессия» служит для расчета параметров уравнения линейной регрессии и проверки его адекватности исследуемому процессу. В диалоговом окне данного режима (рис. 26) задаются следующие параметры: 1. Входной интервал Y – вводится ссылка на ячейки, содержащие данные по результативному признаку Диапазон должен состоять из одного столбца. 2. Входной интервал Х – вводится ссылка на ячейки, содержащие факторные признаки. Максимальное число входных диапазонов (столбцов) равно 16. 3. Метки в первой строке/Метки в первом столбце 4. Уровень надежности – установите данный флажок в активное состояние, если в поле, расположенное напротив флажка, необходимо ввести уровень надежности, отличный от уровня 95 %, применяемого по умолчанию. Установленный уровень надежности используется для проверки значимости коэффициента детерминации R2и коэффициентов регрессии ai. 5. Выходной интервал/Новый рабочий лист/Новая рабочая книга 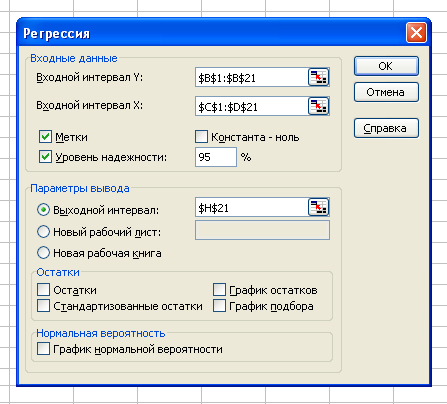 Рис. 26 После того, как мы нажмем на ОК, получим результат, содержащий большое количество информации (рис. 27). Но выберем только те из них, которые потребуются для последующего анализа. Для этого создадим таблицу, в которой поместим расчетные значения коэффициентов регрессии, стандартную ошибку, величины t-критерия и показатели уровня значимости p. Укажем также (ниже таблицы) рассчитанные показатели для самой функции у. 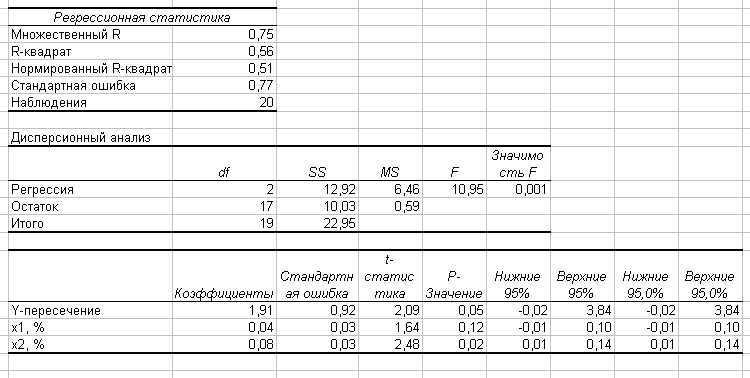 Рис. 27 Таблица 3 Данные регрессионной статистики
Для функции Y: cтандартная ошибка  = 0,77; R2-квадрат = 0,56; R2 (нормированный) = 0,51. Таким образом, для рассматриваемого примера уравнение регрессии (или уравнение прогнозирования) будет иметь следующий вид: y(объем продаж, уп/день) =b0+b1x1+b2x2=1,91+0,04 (доля покупателей, слышавших рекламу, %)+1,62(относительное время работы консультанта, %). Запишем полученное уравнение в окончательной редакции: y=1,91+0,04x1+0,08x2 |