Методичка по работе в MS Excel (статистические методы). Рабочая программа дисциплины Статистические расчеты в ms excel
 Скачать 6.25 Mb. Скачать 6.25 Mb.
|
5.5. Интерпретация коэффициентов регрессииСвободный член (сдвиг) b0, равный 1,91, формально надлежит понимать следующим образом: объем продажи препарата, когда среди покупателей нет тех, кто слышал рекламу, и нет врача консультанта, составляет 1,91 упаковки в день. Однако мы полагаем, что в указанной совокупности исходных данных нет подобных примеров. Поэтому сдвиг b0 следует обсуждать как вспомогательную величину, необходимую для получения оптимальных прогнозов, и не истолковывать ее буквально. Коэффициенты регрессии b1 и b2 следует рассматривать как степень влияния каждой из переменных на уровень продаж препарата, если все другие независимые переменные остаются неизменными. Так, коэффициент b1, равный 0,04, указывает, что (при прочих равных условиях) повышение доли покупателей, слышавших о рекламе препарата на 1 %, приводит к возрастанию его продажи на 0,04 упаковок в день. Анализируя коэффициент b2, можно заметить, что увеличение относительного участия врача-консультанта на 1 % приводит также к повышению продажи, этот прирост составляет почти такую же величину − 0,08 уп/день. Еще раз заметим, что все названные коэффициенты регрессии отражают влияние на исследуемый параметр у только какой-то одной переменной xпри непременном условии, что все другие переменные (факторы) не меняются. Например, применительно к коэффициенту b2 это нужно понимать так: указанное влияние коммерческой помощи консультанта проявляется при условии, что среди покупателей сохраняется неизменной доля тех, кто слышал рекламу. 5.5.1 Ошибки прогнозирования (определение качества регрессионного анализа)Для оценки выполненного регрессионного анализа используют коэффициент детерминации (R2), указывающий, какой процент вариации функции у объясняется воздействием факторов хk. В нашем примере коэффициент детерминации R2 равен 0,56, что составляет 56 %. Этот результат следует толковать так: все исследуемые воздействующие факторы объясняют 56 % вариации анализируемой функции (объема проданных препаратов). Остальное же (44 %, что очень существенно) остается необъясненным и может быть связано с влиянием других, неучтенных факторов. Итак, нами получено уравнение множественной регрессии, коэффициенты которого bi формально показывают, как и в каком направлении действуют (пока лишь вероятно!) исследуемые факторы хkiи какой процент изменчивости функции у объясняется влиянием именно этих факторов. Теперь нам надлежит определить статистическую значимость полученного аналитического выражения. 5.5.2 Проверка значимости моделиРешение принимается на основе коэффициента детерминации R2. В этом случае имеющуюся расчетную величину R2расч (рис.27) необходимо сравнить с табличными (критическими) значениями R2крит для соответствующего уровня значимости (повторим еще раз, обычно это 0,05). Если окажется, что R2расч> R2крит, то с упомянутой степенью вероятности (95 %) можно утверждать, что анализируемая регрессия является значимой. Напомним, что, по нашим расчетам, коэффициент детерминации R2расч составляет 0,56, или 56 %. Таблица для тестирования на уровне значимости 5 % в случае выборки n = 20 и числа переменных k = 2 дает критическое значение R2крит = 0,297. Поскольку выполняется соотношение R2расч> R2крит, то с вероятностью 95 % можно утверждать о наличии значимости данного уравнения регрессии. 5.5.3. Проверка на адекватность коэффициентов регрессииПроверку на адекватность коэффициентов регрессии рекомендуется проводить по следующим эквивалентным методам. 1. Использование t-критерия. Анализируемый коэффициент считается значимым, если его t-критерий по абсолютной величине превышает 2,00 (точнее 1,96), что соответствует уровню значимости 0,05. В нашем примере имеем для коэффициентов b0, b1 и b2 следующие показатели критерия Стьюдента: t b0 = 2,09; t b1 = 1.64 и t b2 = 2.48. Из всего вышесказанного следует, что значимыми оказываются коэффициенты b0 и b2 нашего уравнения. 2. Использование уровня значимости. В этом случае оценка проводится путем анализа показателя р. Коэффициент признается значимым, если рассчитанное для него р-значение (эти данные выдает Excel) меньше (или равно) 0,05 (т.е. для 95 %-ной доверительной вероятности). Показатель р составляет для коэффициентов следующие величины: р b0 = 0,05; р b1= 0,12 и р b2 = 0,02. Эти данные позволяют также заключить, что из рассмотренных коэффициентов статистически значимыми являются первый и третий. В целом же проведенный регрессионный анализ дает нам основание сделать вывод о том, что влияние на продажи работы врача-консультанта значимо. Вместе с тем необходимо учитывать, что нами явно не приняты во внимание все факторы (вспомним про 44 %, приходящихся на неучтенные причины), что требует проведения дополнительных исследований. 5.6. Поиск закономерностей для качественных данных. Анализ «хи-квадрат»Критерий хи-квадрат используют для проверки гипотез о качественных данных, представленных не числами, а категориями. Здесь принято оперировать подсчетом частоты (поскольку ранжирование или арифметические действия выполнять невозможно). Критерий (тест) «хи-квадрат» основан на частотах, которые представляют собой количество объектов выборки, попадающих в ту или иную категорию. Суть показателя хи-квадрат (χ2): он измеряет разницу между наблюдаемыми (экспериментальными) частотами fЭи ожидаемыми (теоретическими) частотами fТ. Конкретно он рассчитывается как сумма квадратов разности этих частот, выраженная в долях частоты теоретической. Это утверждение можно записать следующим образом: 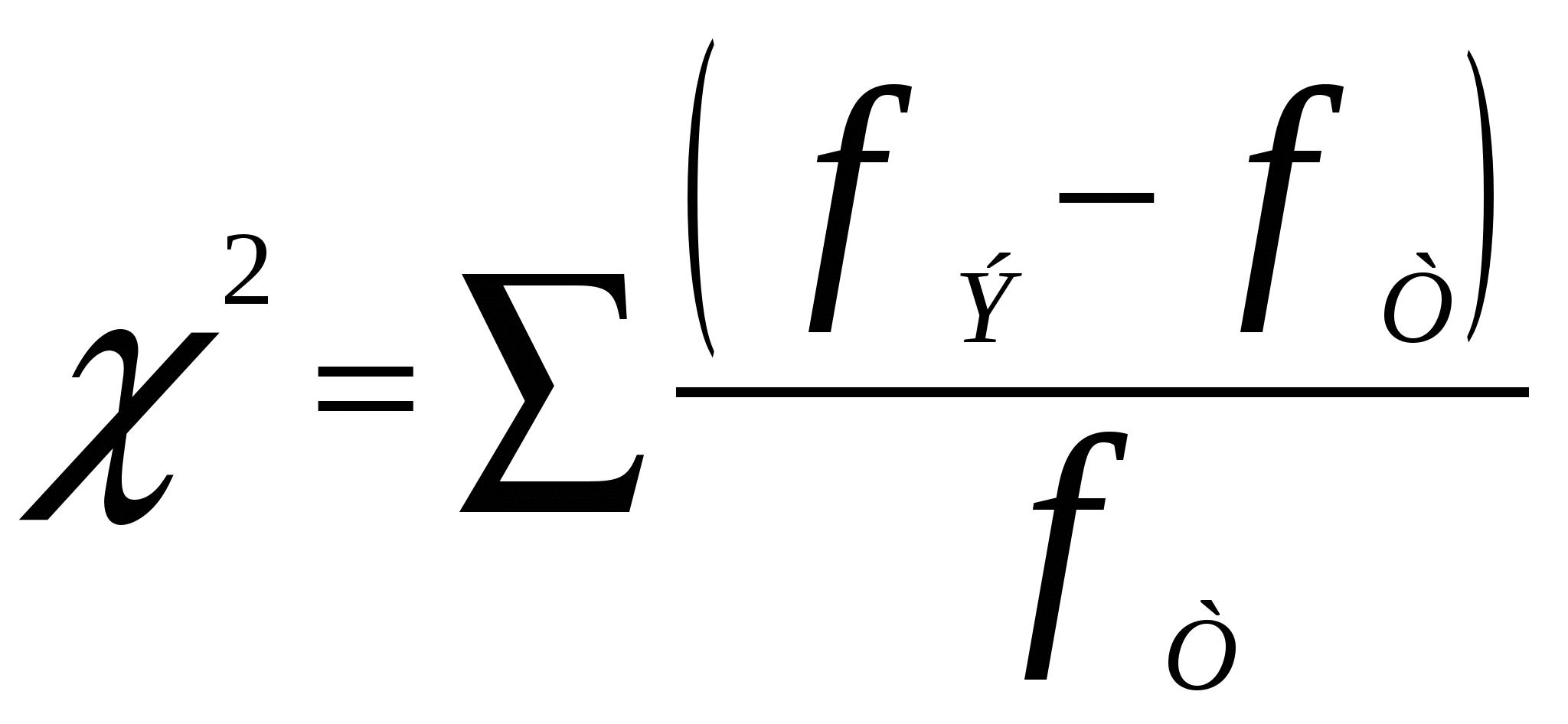 Использование этого статистического подхода рассмотрим на следующем примере. Мы решили провести маркетинговое исследование, чтобы уяснить, какую марку минеральной воды предпочитают мужчины и женщины. Для каждой покупки фиксировались две качественные переменные – марка воды и пол покупателя. В качестве продаваемой воды фигурировали «Нарзан», «Ессентуки» и «Тагарская». Полученные данные статистического опроса представлены в табличной форме (табл.4), в которой для каждого вида минеральной воды указано количество совершаемых покупок тем или иным покупателем. Необходимо дать заключение по итогам статистической проверки по критерию «хи-квадрат», т.е. сформулировать вывод и пояснить результат с практической точки зрения – определить, какую рыночную стратегию необходимо принять, т.е., на какого покупателя и на какую марку минеральной воды необходимо ориентироваться. Таблица 4.– Экспериментальные данные о результатах опроса посетителей аптеки
Чисто визуально трудно ответить, есть ли взаимосвязь между этими признаками: разными категориями покупателей и марками минеральной воды. Поэтому необходимо дать анализ распределения частот в таблице по строкам и графам. При этом исходят из следующего положения. Если признак, положенный в основу группировки по строкам (марка минеральной воды), не зависит от признака, положенного в основу группировки по столбцам (пол покупателя), то в каждой строке (столбце) распределение частот должно быть пропорционально распределению их в итоговой строке (столбце). Такое распределение можно рассматривать как теоретическое (ожидаемое), частоты которого рассчитаны в предположении отсутствия связи между изучаемыми совокупностями. Рассчитаем ожидаемые частоты внутри таблицы пропорционально распределению частот в итоговой строке. Так, «Нарзан» как одна из марок минеральной воды в зависимости от поведения посетителей аптеки по частоте попадания в категории «Мужчины» и «Женщины» имеет следующие показатели: Для второй строки, т.е. для воды «Ессентуки», эти показатели имеют следующие значения: Для третей строки – категория «Тагарская»: Полученные результаты поместим в таблицу 5. Таблица 5. – Теоретические данные о результатах опроса посетителей аптеки
5.6.1. Анализ «хи-квадрат. Технология расчетаПеренесем данные обеих таблиц в рабочий лист Excel (рис.28). Анализ хи-квадрат выполним с помощью функции ХИ2тест. Для этого используем Мастер функций/ Статистические / ХИ2тест. В ячейку В11 поместим результаты теста. При заполнении диалогового окна в текстовом поле фактического интервала укажем адрес ячеек С4:D6, в которых находятся экспериментальные данные по частотам (табл.4). Соответственно в текстовом поле ождаемого интервала укажем диапазон H4:I6, содержимое которого отражает теоретические значения частот (табл.5). 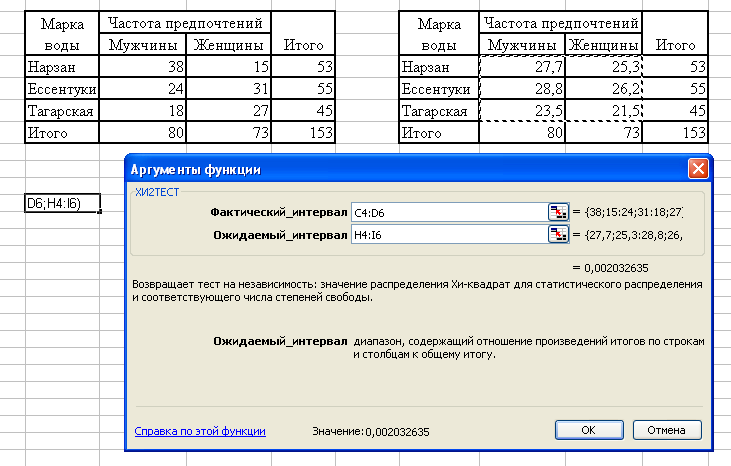 Рис.28 В окончательном виде в ячейке В11 будет находиться следующий показатель, а именно: 0,002. Как же следует трактовать полученный результат? Тезис о независимости обсуждаемых параметров (вид минеральной воды и пол покупателя) можно было бы принять, если бы уровень значимости α был бы меньше 0,002. Но для 95 %−ной вероятности (даже 99-процентной) установленные значения α (0,05 и 0,01) превышают 0,002. Это говорит о высокой степени значимости, следовательно, указанные качественные переменные являются зависимыми друг от друга. Другими словами, предпочтение в выборе той или иной марки минеральной воды определяется полом покупателя. Литература
| ||||||||||||||||||||||||||||||||||||||||||||
