Методичка по работе в MS Excel (статистические методы). Рабочая программа дисциплины Статистические расчеты в ms excel

• Название: Рабочая программа дисциплины Статистические расчеты в ms excel
• Анкор: Методичка по работе в MS Excel (статистические методы).doc
• Дата: 30.01.2017
• Размер: 6.25 Mb.
• Имя файла: Методичка по работе в MS Excel (статистические методы).doc
• Тип: Рабочая программа; #1241
• Категория: Медицина
• страница: 2 из 9

1.3. Работа с мастером функций

Наряду с надстройкой Пакет анализа в практике статистической обработки могут широко применяться статистические функции Microsoft Excel. В состав Excel входит библиотека, содержащая 78 статистических функций, ориентированных на решение самых рааличных задач прикладного статистического анализа.

Причем одну часть статистических функций можно рассматривать как своего рода элементарные составляющие того или иного режима надстройки Пакет анализа, другую часть – как уникальные функции, не дублирующиеся в надстройке Пакет анализа.

Тем не менее, функции, входящие и в первую часть, и во вторую часть, имеют самостоятельное значение и могут применяться автономно при решении конкретных статистических задач.

Работать со статистическими функциями Excel, как, впрочем, и с функциями из других категорий, удобнее всего с помощью мастера функций. При работе с мастером функций необходимо сначала выбрать саму функцию, а затем задать ее отдельные аргументы. Запустить мастер функций можно командой Функция... из меню Вставка, или щелчком по кнопке вызова мастера функций f_x, или активизацией комбинации клавиш Shift+F3

Для упрощения работы с мастером отдельные функции сгруппированы по тематическому признаку. Тематические категории представлены в области Категория (рис. 5). В категории Полный алфавитный перечень содержится список всех доступных Б программе функций, К категории 10 недавно использовавшихся относятся десять применявшихся последними функций. Поскольку пользователь во время работы применяет ограниченное число функций, то с помощью этой категории можно получить быстрый доступ к тем из них, которые необходимы в повседневной работе.

Чтобы задать статистическую функцию, сначала необходимо выбрать категорию Статистические, При перемещении строки выделения по списку функций под областями Категория и Функция будет представлен пример, иллюстрирующий способ задания выбранной статистической функции с краткой информацией о ней.

Если краткой информации недостаточно, щелкните в диалоговом окне по кнопке Справка. На экране появится помощник и предложит помощь. Щелкните по кнопке Справка по выделенной функции, и на экране будет представлена соответствующая страница справочной подсистемы.

После выбора функции щелкните по кнопке ОК для перехода в следующее диалоговое окно мастера функций, в котором должны быть заданы аргументы. В этом диалоговом окне мастер подсказывает пользователю, какие аргументы следует указать обязательно (обязательные аргументы), а какие - опционально (необязательные аргументы). Задать аргументы можно различными способами, наиболее удобные из них предлагает помощник. После задания всех аргументов функции щелкните по кнопке ОК, чтобы в ячейке появились результаты выполнения функции.

.

Рис. 5.

2. Определение характера распределения и формирование выборки

2.1. Теоретические основы группировки

Результаты сводки и группировки материалов статистического наблюдения оформляются в виде таблиц и статистических рядов распределения.

Группировка – объединение единиц статистической совокупности в количественные однородные группы в соответствии со значениями одного или нескольких признаков.

Статистический ряд распределения представляет собой упорядоченное распределение единиц изучаемой совокупности по определенному варьирующему признаку. Он характеризует состояние (структуру) исследуемого явления, позволяет судить об однородности совокупности, единицах ее изменения, закономерностях развития наблюдаемого объекта. Построение рядов распределения является составной частью сводной обработки статистической информации.

В зависимости от признака, положенного в основу образования ряда распределения, различают атрибутивные и вариационные ряды распределения. Последние, в свою очередь, в зависимости от характера вариации признака делятся на дискретные (прерывные) и интервальные (непрерывные) ряды распределения.

Пример дискретного ряда: Распределение медицинских халатов, реализованных магазином за месяц, по размерам. Размер халата Число проданных халатов, шт. 44 12 46 31 48 127 50 215 52 164 54 91 56 47 58 28 60 11 Итого 726

Пример интервального ряда: Распределение покупок в аптеке по сумме. Сумма покупки, руб. Число покупок До 50 37 50,1-100 78 100,1-150 111 150,1-200 105 200,1-250 68 Свыше 250 49 Итого 448

Группировка осуществляется поэтапно. Вначале определяется примерное число групп, затем величина интервала. Строится первый вариант группировки, который при необходимости уточняется. Для определения числа групп может применяться формула Стерджесса:

,

где N – численность совокупности, r – число групп.

Величина интервала определяется по формуле: ,

где x_max, x_min – соответствующие максимальное и минимальное значения признаков совокупности, r – величина интервала. Полученный результат округляется.

Равные интервалы группировки применяются для однородных совокупностей, а для социально-экономических явлений чаще применяются неравноинтервальные группировки. Если крайнее значение единиц совокупности значительно отличается по величине от остальных, применяются группировки с открытыми границами интервалов.

Первый интервал с открытой нижней границей, последний интервал с открытой верхней границей. Величина первого интервала принимается равной величине следующего за ним интервала (не более чем). Величина последнего интервала с открытой верхней границей принимается равной величине предпоследнего интервала.

Различают абсолютные и относительные частотные характеристики.

Абсолютная характеристика – частота, показывает, сколько раз встречается в совокупности данный вариант ряда. Достоинство частоты – простота, недостаток – невозможность сравнительного анализа рядов распределения разной численности.

Для подобных сравнений применяют относительные частоты или частости, которые рассчитываются по формуле: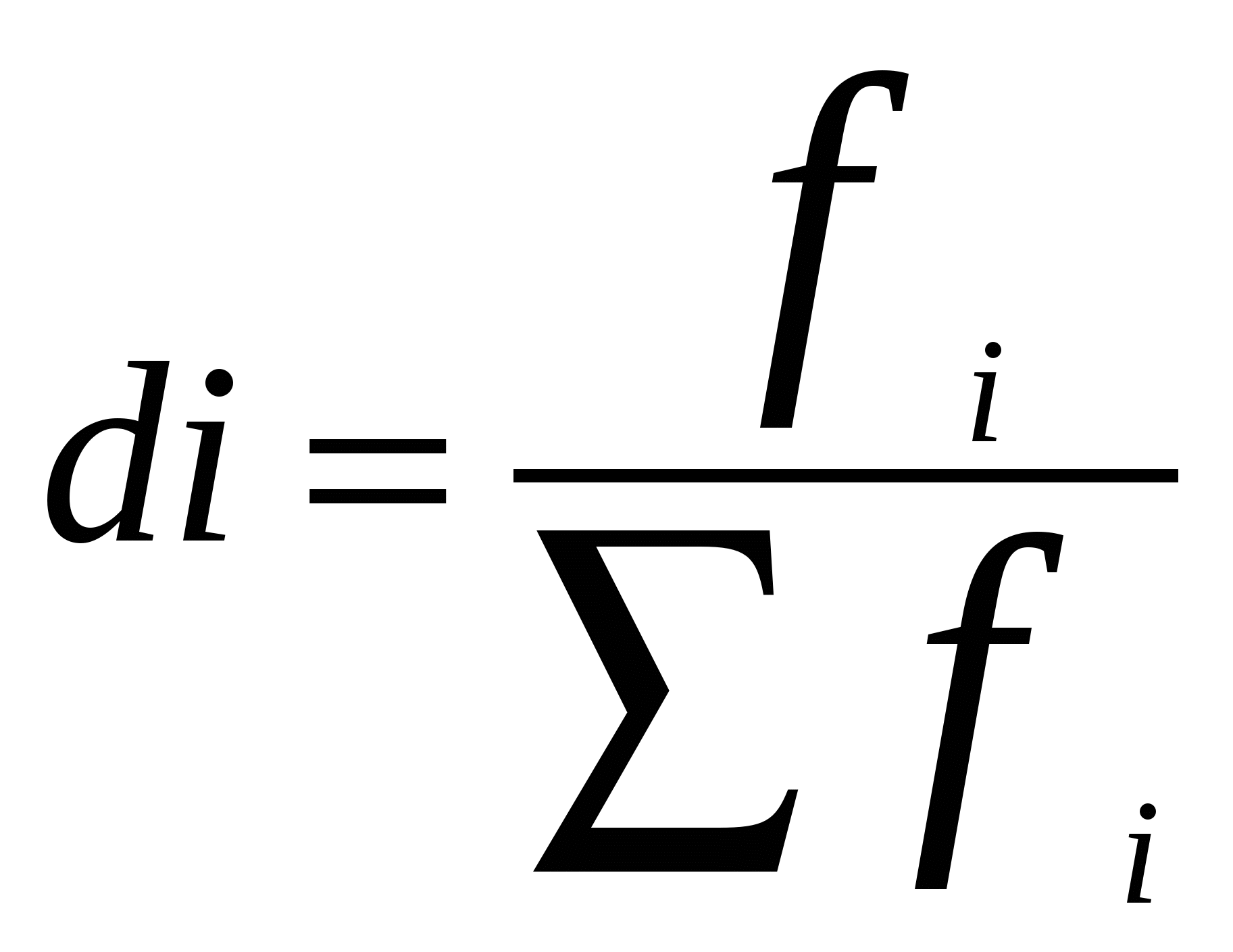

, ,

где N – численность совокупности.

Это относительная величина структуры (по форме).

Сумма частостей равна 1.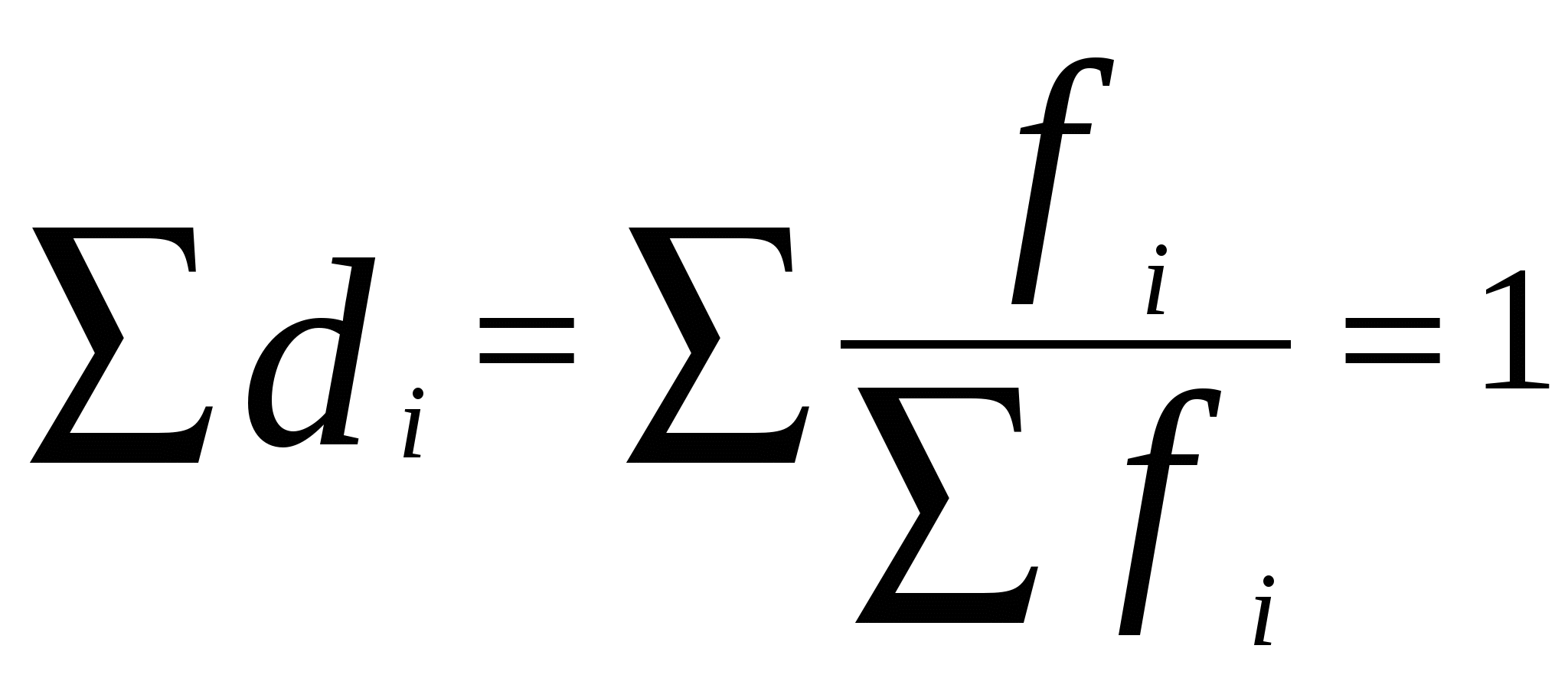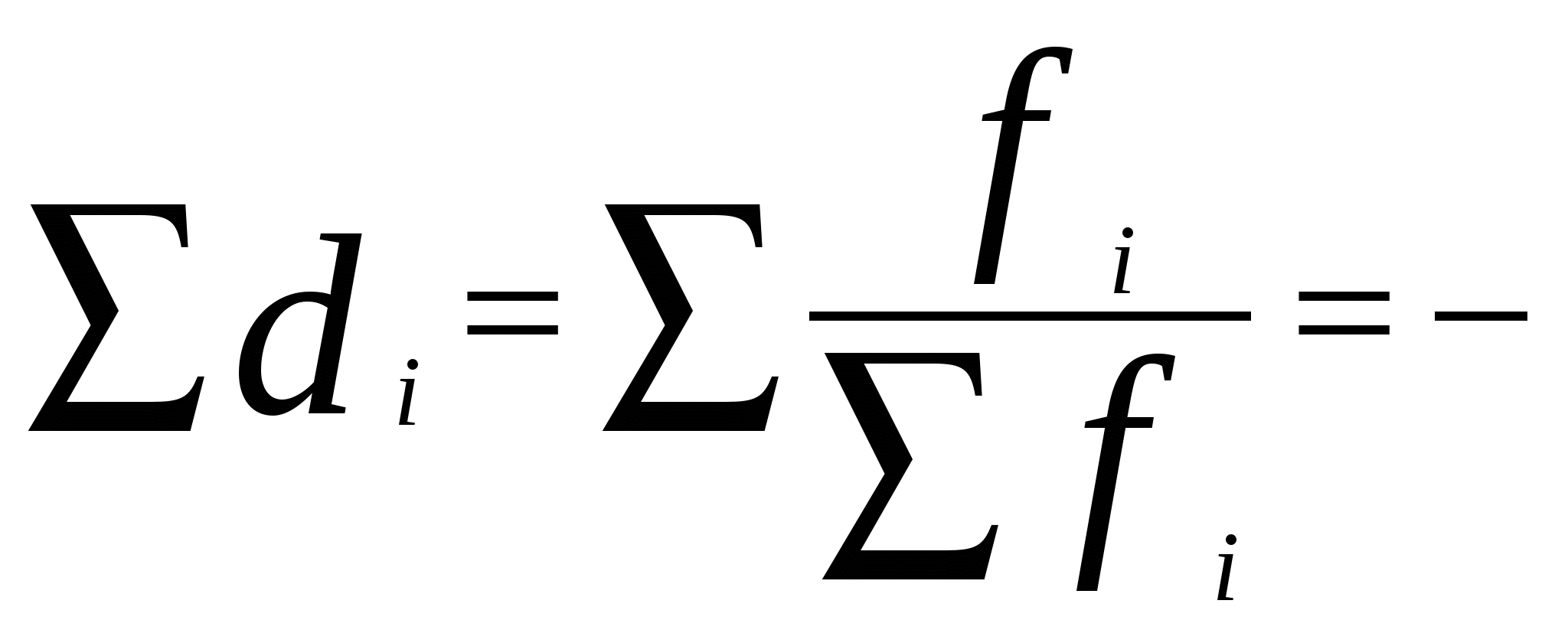



Если частости выражены в процентах или в промилях их суммы равны соответственно 100 или 1000.

В неравных интервальных рядах распределения частотные характеристики зависят не только от распределения вариантов ряда, но и от величины интервала при прочих равных условиях расширение границ интервала приводит к увеличению наполненности групп.

Для анализа рядов распределения с неравными интервалами используют показатели плотности:

Абсолютная плотность: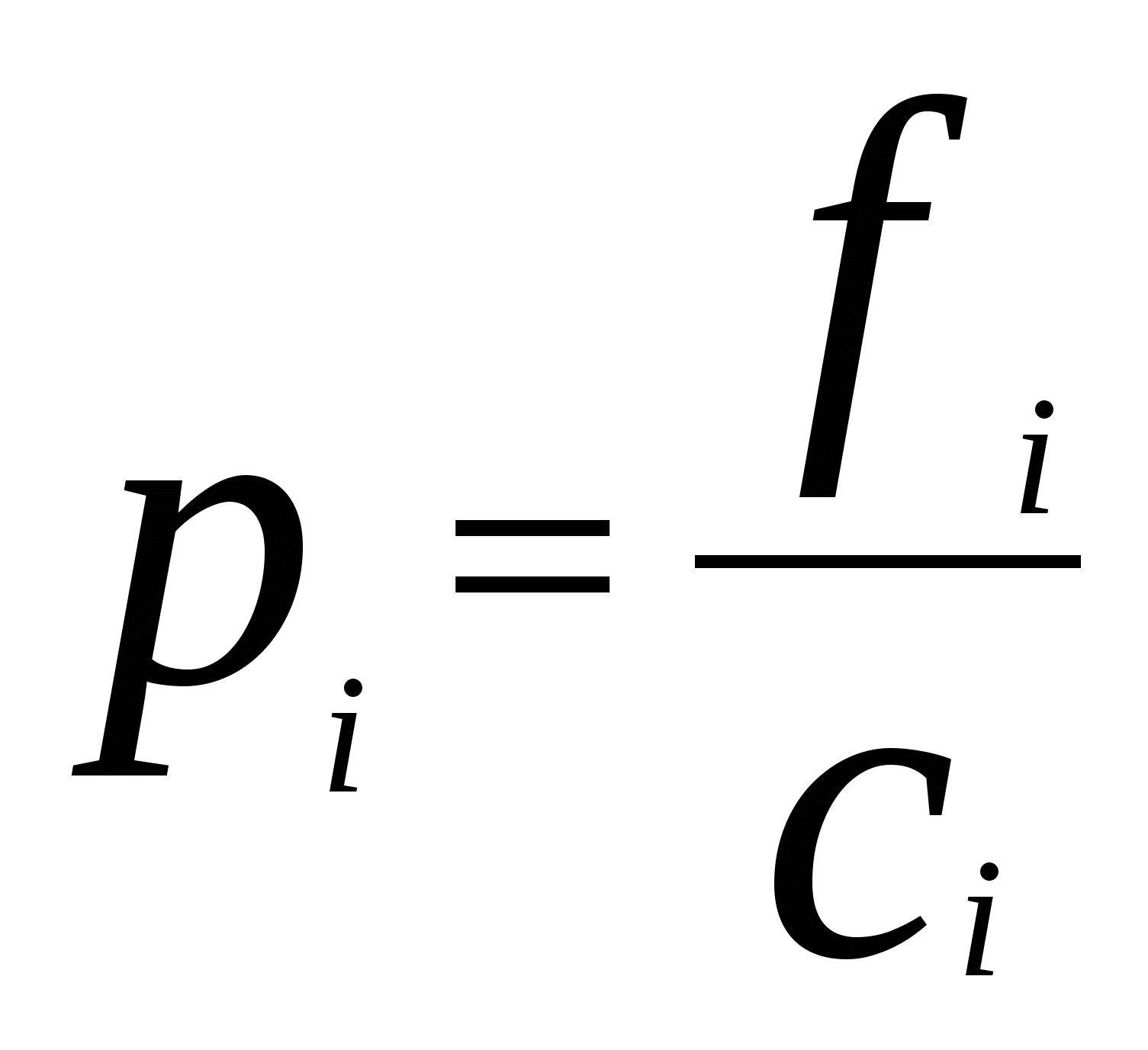

где f_i – частота, c_i - величина интервала – показывает, сколько единиц в совокупности приходится на единицу величины соответствующего интервала. Абсолютная плотность позволяет сопоставлять между собой насыщенность различных по величине интервалов ряда. Абсолютные плотности не позволяют, однако, сравнивать ряды распределения разной численности.

Для подобных сравнений применяются относительные плотности: 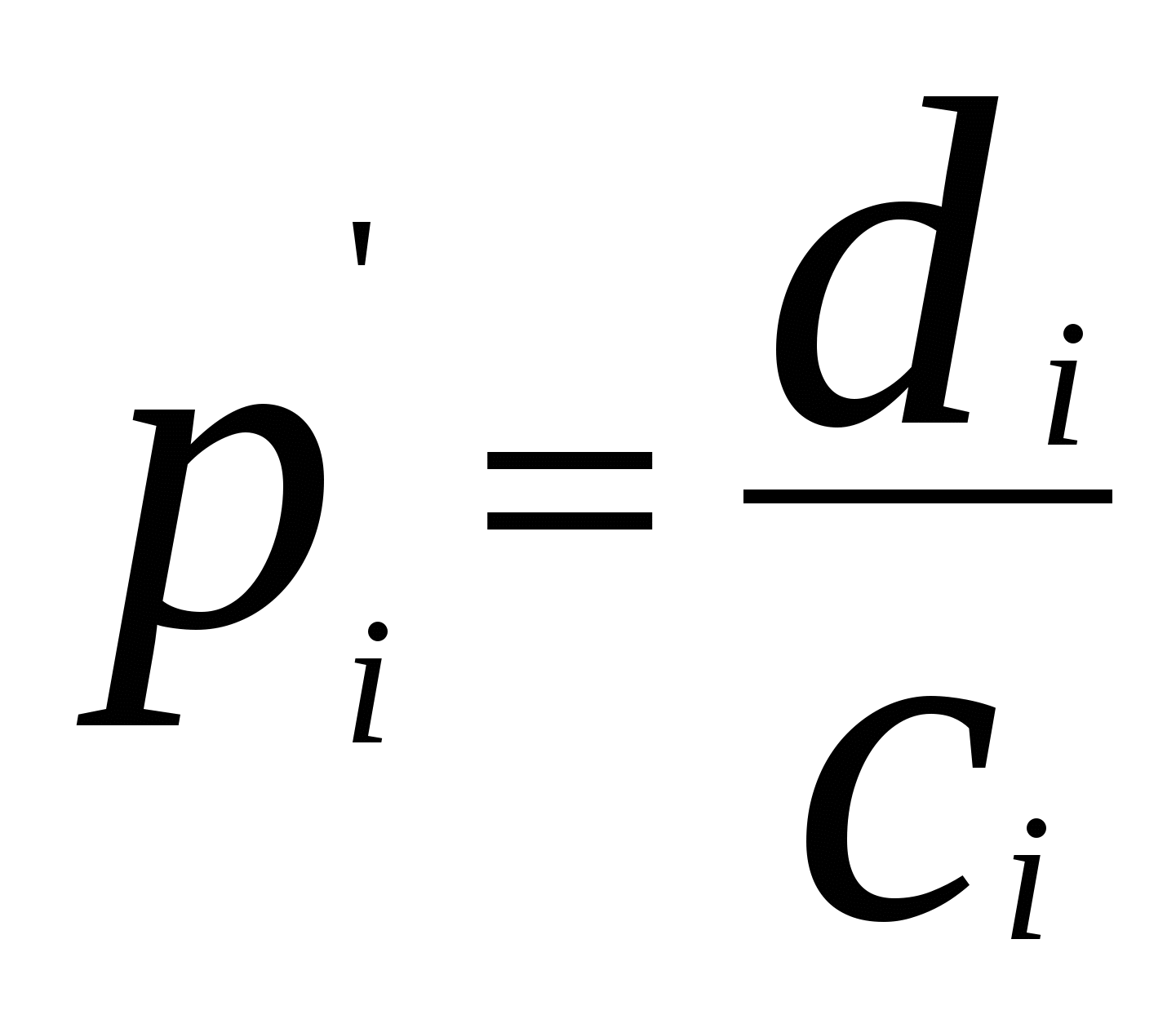, где d_i – частости (доли), c_i - величины соответствующих интервалов – показывает, какая часть (доля) совокупности приходится на единицу величины соответствующего интервала. Удобнее всего ряды распределения анализировать с помощью их графического изображения, позволяющего судить о форме распределения. Наглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма.

Полигон используется для изображения дискретных вариационных рядов. При построении полигона в прямоугольной системе координат по оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака, а по оси ординат наносится шкала частот, т. е. число случаев, в которых встретилось то или иное значение признака. Полученные на пересечении абсцисс и ординат точки соединяют прямыми линиями, в результате чего получают ломаную линию, называемую полигоном частот. Например, на рис. 6. приведено распределение числа студентов по успеваемости и полигон частот для данного распределения. Для построения полигона воспользуемся мастером диаграмм Microsoft Excel (режим «График»).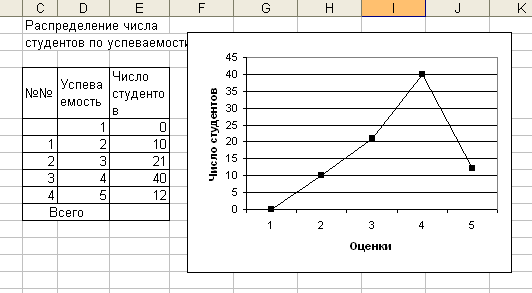



Рис. 6
Для изображения интервальных вариационных рядов распределений применяются гистограммы. При этом на оси абсцисс откладываются значения интервалов, а частоты изображаются прямоугольниками, построенными на соответствующих интервалах. В результате получается гистограмма – график, на котором ряд распределения представлен в виде смежных друг с другом областей. Для характеристики рядов распределения применяют так же графики накопленных частот или кумуляты.

Кумулята позволяет определить, какая часть совокупности обладает значениями изучаемого признака не превышающими заданного предела, а какая часть – наоборот – превышает этот предел.