Методичка по работе в MS Excel (статистические методы). Рабочая программа дисциплины Статистические расчеты в ms excel

• Название: Рабочая программа дисциплины Статистические расчеты в ms excel
• Анкор: Методичка по работе в MS Excel (статистические методы).doc
• Дата: 30.01.2017
• Размер: 6.25 Mb.
• Имя файла: Методичка по работе в MS Excel (статистические методы).doc
• Тип: Рабочая программа; #1241
• Категория: Медицина
• страница: 7 из 9

5. Статистические методы изучения взаимосвязей явлений и процессов

5.1. Корреляционный анализ. Краткие сведения из теории статистики

В экономических исследованиях одной из важных задач является анализ зависимостей между изучаемыми переменными. Зависимость между переменными может быть либо функциональной, либо статистической. Для оценки тесноты и направления связи между изучаемыми переменными при их стохастической зависимости пользуются показателями корреляции.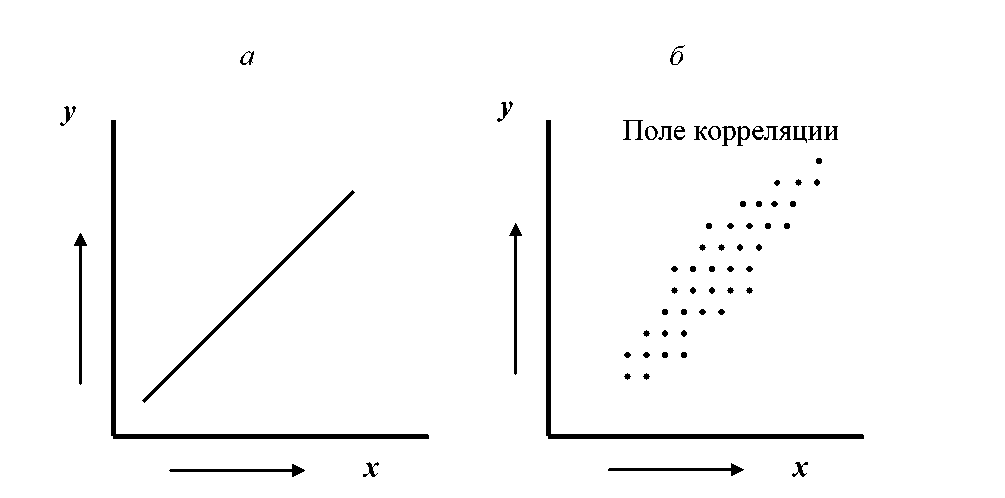




Рис. 22. Зависимость функциональная (а) и статистическая (б)
В 1889 г. Ф. Голтон высказал мысль о коэффициенте, который мог бы измерить тесноту связи между двумя коррелируемыми признаками. В начале 90-х гг. XIХ в. Пирсон, Эджворт и Велдон получили формулу линейного коэффициента корреляции: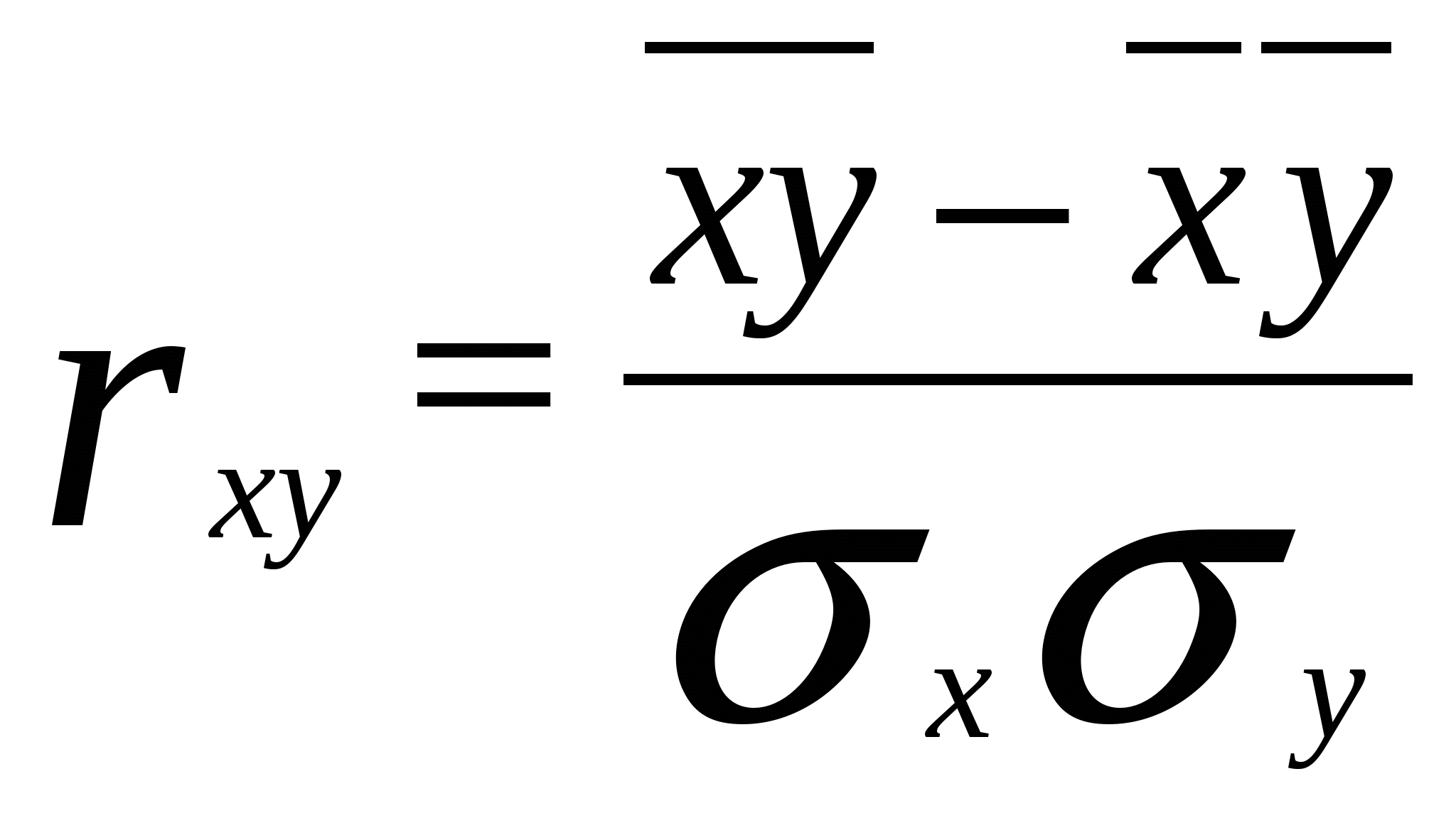



Линейный коэффициент корреляции характеризует степень тесноты не всякой, а только линейной зависимости. Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать (или убывать) по линейному закону. Эта тенденция к линейной зависимости может быть более или менее ярко выраженной, т. е. более или менее приближаться к функциональной. Если случайные величины X и Y связаны точной линейной функциональной зависимостью y=ax+b то r_xy=±1. В общем случае, когда величины X и Y связаны произвольной вероятностной зависимостью, линейный коэффициент корреляции принимает значение в пределах -1 < r_xy < 1, тогда качественная оценка тесноты связи величин X и Y может быть выявлена на основе шкалы Чеддока (табл. 1).
Таблица 1

Теснота связи	Значение коэффициента корреляции при наличии:
	прямой связи	обратной связи
Слабая	0,1-0,3	(-0,1)-(-0,3)
Умеренная	0,3 - 0,5	(-0,3)-(-0,5)
Заметная	0,5 - 0,7	(-0,5)-(-0,7)
Сильная	0,7 - 0,9	(-0,7) - (-0,9)
Очень сильная	0,9 - 0,99	(-0,9) - (-0,99)

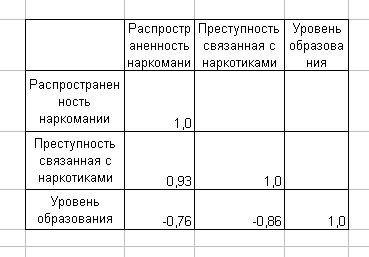
5.2. Расчет коэффициента корреляции. Технология работы.

Режим работы «Корреляция» предназначен для расчета генерального и выборочного коэффициентов корреляции соответственно на основе генеральных и выборочных данных. Пример: На рабочем листе Excel сформирована таблица (рис. 23). Изучалась зависимость между распространенностью наркомании, преступностью и уровнем образования в некоторых городах России. По выборочным данным, представленным в таблице, требуется установить наличие взаимосвязи между показателями.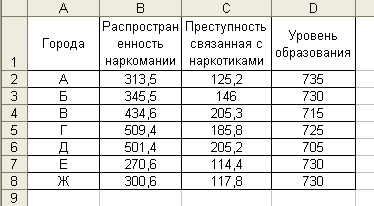


Рис. 23

Значение параметров в диалоговом окне и полученная корреляционная матрица выглядят следующим образом (рис. 24).


Рис. 24

Как видно из корреляционной матрицы на рис. 24, между парами всех исследуемых показателей существуют стохастические связи. Характер всех выявленных связей различен и состоит в следующем:

Связь «преступность, связанная с оборотом наркотиков» и «распространенность наркомании» является положительной и очень сильной (r_xy = 0,93), связь «уровень образования» – «уровень преступности» является сильной и обратной (r_xy = -0,76), т. е. с

повышением уровня образования уровень преступности уменьшается; связь «уровень

образования» - «распространенность наркомании» также является сильной и обратной

(r_xy = - 0,86), т. е. с увеличением уровня образования распространенность наркомании уменьшается.

Статистическую оценку коэффициента парной корреляциипроводят путем сравнения его абсолютной величины с табличным (или критическим) показателем r_xy крит, значения которого отыскиваются из специальной таблицы. Если окажется, что r_xy расч ≥ r_xy крит, то с заданной степенью вероятности (обычно 95 %) можно утверждать, что между рассматриваемыми числовыми совокупностями существует значимая линейная связь. Или по-другому − гипотеза о значимости линейной связи не отвергается. В случае же обратного соотношения, т.е. при r_xy расч < r_xy крит, делается заключение об отсутствии значимой связи. Так, в нашем примере r_xy крит = 0,754, поэтому с вероятностью 95% мы можем говорить о достоверной линейной связи между изучаемыми показателями.

Часто корреляцию и причинную обусловленность считают синонимами. Этот тезис имеет определенные основания, поскольку если нечто является причиной чего-либо другого, то можно говорить о связи первого и второго и, следовательно, об их коррелированности (например, действие и результат, проверка и качество, капиталовложения и прибыль, окружающая среда и прибыль).

Однако корреляция может быть и без причинной обусловленности. Это можно представить так: корреляция − лишь число, которое указывает на то, что большим значениям одной переменной соответствуют большие (или же меньшие) значения другой переменной. Корреляция не может объяснить, почему эти две переменные связаны между собой. Так, корреляция не объясняет, почему капиталовложения порождают прибыль (или наоборот). Корреляция просто констатирует, что между этими величинами существует определенное соответствие. И не более того.

Одним из возможных оснований для существования «корреляции без причинной обусловленности» является наличие некоторого скрытого, ненаблюдаемого, третьего фактора, который «маскируется» под другую переменную. В результате фиксируется так называемая «ложная корреляция».

В истории статистики известен один классический пример. Он касается курьезного исследования под условным названием «Аисты приносят детей». Так, в шведской столице в течение 73 лет регистрировалось число новорожденных в год (у) и число аистов (х), которых содержало население. Указанные данные были сведены в таблицу, и по ним был рассчитан коэффициент парной корреляции. Он оказался близок к единице, так что формально никакой статистики и не требовалось для проверки. Все экспериментальные точки аккуратно улеглись на прямую, т.е. практически указанную связь следовало бы толковать как чисто функциональную.

Поскольку утверждение, содержащее в упомянутом тезисе, довольно сомнительное, было решено поискать другое разумное объяснение. Оказалось, что одновременные синхронные изменения числа аистов и числа детишек объясняются изменением среднего уровня жизни жителей Стокгольма.

Эта переменная первоначально не являлась предметом рассмотрения, отчего и случился такой забавный курьез вследствие ложной корреляции.

В качестве статистического показателя может быть использован также коэффициент (индекс) детерминации (причинности) R², который равен квадрату коэффициента корреляции (r²). Он показывает, в какой мере изменчивость у (результативного признака) объясняется поведением х (факторного признака), или иначе: какая часть общей изменчивости у вызвана собственно влиянием х. Этот показатель вычисляется путем простого возведения в квадрат коэффициента корреляции. Тем самым доля изменчивости у, определяемая выражением 1− R², оказывается необъясненной. Коэффициент детерминации R² для нашего примера равен 0,93²=0,865 или 86,5%. Величина показателя свидетельствует о том, что 86,5% (вариации) распространенности наркомании объясняются уровнем преступности, связанной с наркотиками. Остальные 13,5% объясняются какими-то другими причинами.

Величина этого коэффициента меняется в пределах от 0 до 1. Чем ближе он к единице, тем, следовательно, меньше в нашей модели процесса влияние неучтенных факторов.