Методичка по работе в MS Excel (статистические методы). Рабочая программа дисциплины Статистические расчеты в ms excel

• Название: Рабочая программа дисциплины Статистические расчеты в ms excel
• Анкор: Методичка по работе в MS Excel (статистические методы).doc
• Дата: 30.01.2017
• Размер: 6.25 Mb.
• Имя файла: Методичка по работе в MS Excel (статистические методы).doc
• Тип: Рабочая программа; #1241
• Категория: Медицина
• страница: 4 из 9

2.3. Технология работы при формировании выборки

Пример. Оптовая фирма, торгующая изделиями медицинского назначения, решила для посетителей своего Web-сайта организовать лотерею по рассылке каталогов новой продукции. Для этого на сайте фирмы реализован счетчик посещений и предлагается (по желанию пользователя) заполнить электронный бланк с указанием своего почтового адреса. Отбор посетителей производится на основе показаний счетчика посещений за неделю. Для этого случайным образом отбираются пять показаний счетчика и проверяются соответствующие им регистрации посетителей. Если посетитель не указал своего адреса –каталог не высылается, в противном случае – высылается. При этом если одно и то же показание счетчика попало в выигрышную выборку несколько раз или несколько «выигрышных визитов» на сайт осуществил один и тот же посетитель, каталог высылается по одному и тому же адресу в соответствующем количестве экземпляров. Рассмотрим следующую ситуацию. За последнюю неделю на сайте фирмы было зарегистрировано 25 посещений (показания счетчика увеличились с 360 до 385). Исходная информация, параметры расчетов и результаты приведены на рис. 10.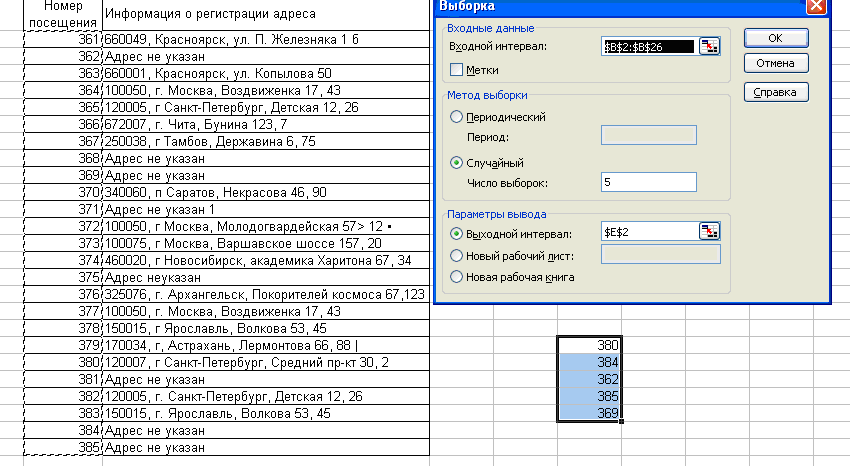



Рис. 10

Как видно из рисунка за последнюю неделю выигрышными оказались 362, 369, 380, 384, 385 посещения. Но каталог будет выслан только номеру 380 по указанному адресу. В остальных случаях рассылка проводиться не будет, т.к. клиентом не был указан адрес.

Пример. Предприятием «Импульс» за месяц было выпущено 150 медицинских приборов, которым были присвоены заводские номера с 10001-го по 10150-й включительно. Все приборы выпускаются на основании технической документации, в соответствии с которой дисперсия чувствительности приборов не превышает 25 мкВ²/м². Необходимо на основе схемы повторного собственно-случайного отбора сформировать контрольную выборку, чтобы с уровнем надежности не менее 95 % предельная ошибка выборки не превышала 3 мкВ²/м².

В примере 3.3.2, в отличие от примера 3.3.1, важным является момент определения необходимого объема выборки, чтобы она была репрезентативной. Для определения величины объема выборки воспользуемся формулой: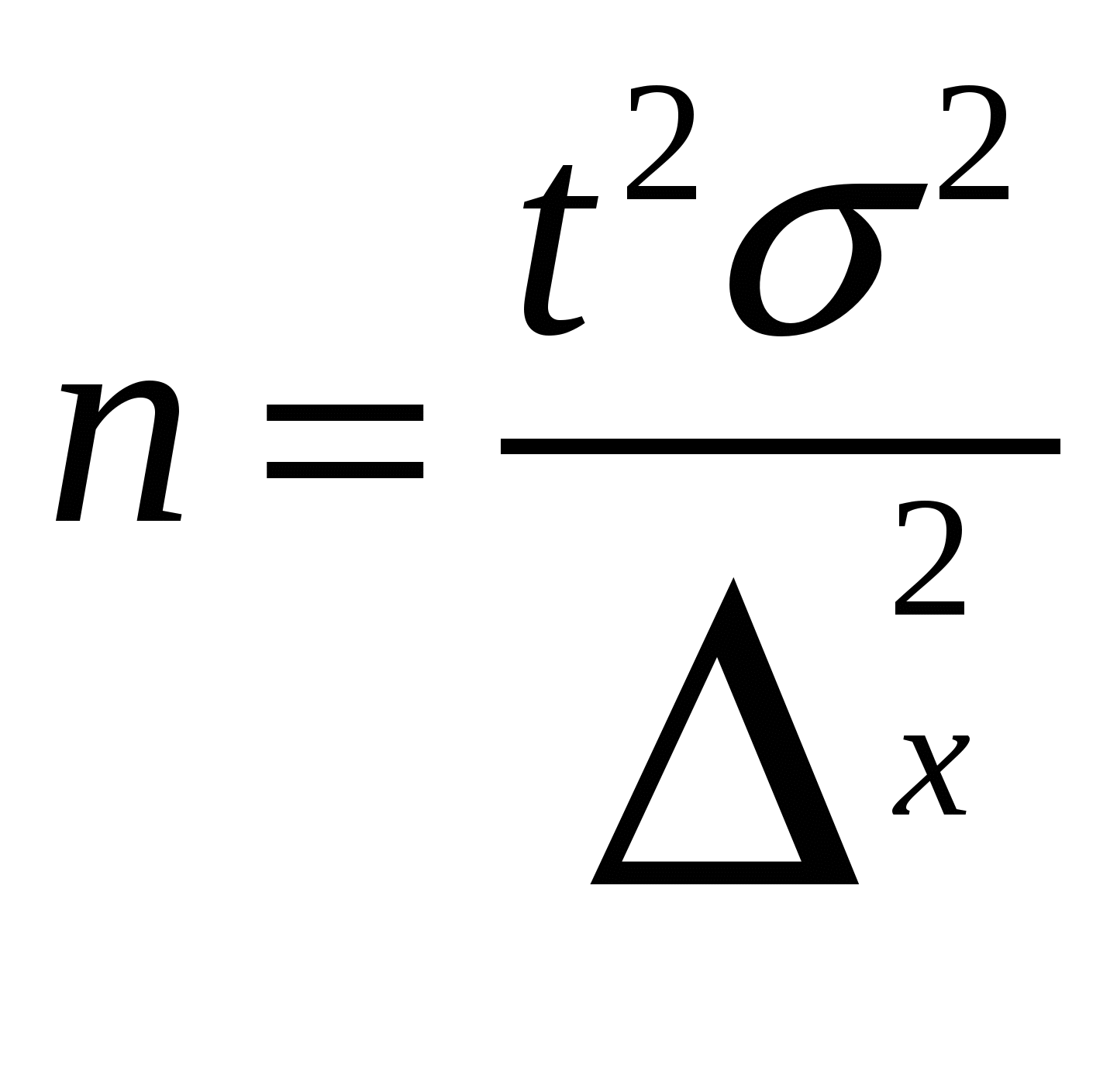



Подставляя в нее исходные данные, получаем: n=

Примечание: В расчете необходимого объема выборки используется коэффициент доверия t, для вычисления которого в Microsoft Excel предусмотрена функция СТЬЮДРАСПОБР. Коэффициент доверия t рассчитывается по формуле =СТЬЮДРАСПОБР(0,05;149), где 0,05 = 1-0,95 - требуемый уровень значимости, 149 = 150-1 – число степеней свободы.

Таким образом, минимально допустимый объем выборки составляет 11 приборов. При меньшем объеме выборка не будет репрезентативной. Последующая технология решения задачи аналогична технологии решения задачи в примере 3.3.1. При этом в поле Число выборок вводится рассчитанное значение необходимого объема выборки г =11 (рис. 3.3.2).

Для быстрого ввода исходных данных рекомендуем воспользоваться таким техническим приемом, как копирование ячеек с помощью меню Правка, Заполнить, Прогрессия арифметической прогрессии с шагом 1.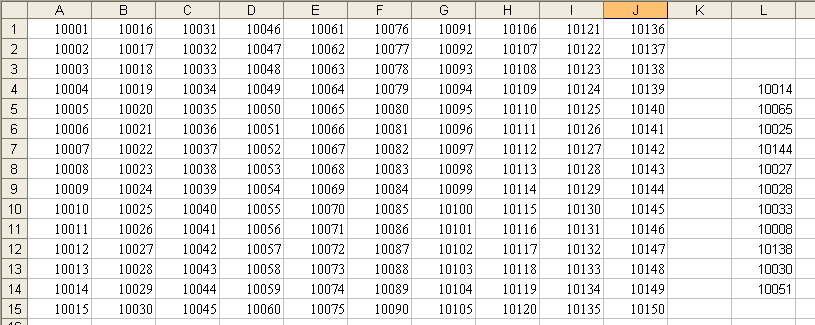

Рис. 11
Результатом решения задачи явилась выборка из 11 приборов с заводскими номерами: 10008, 10014, 10025, 10027, 10028, 10030, 10033, 10051, 10065, 10138, 10144. Так как в выборке номера приборов не повторяются, то каждый прибор подвергается проверке только один раз.

3. Характеристика статистической совокупности. Средние величины. Меры рассеяния

Статистическая информация представляется совокупностью данных, для характеристики которых используются разнообразные показатели, называемые показателями описательной статистики.

Уровень образования, прожиточный минимум, дифференциация доходов населения, среднее число детей в семье, средний курс доллара и мера его колебания за определенный интервал времени, таблицы продолжительности жизни.

Показатели описательной статистики можно разбить на несколько групп:

1. Показатели положения описывают положение данных на числовой оси. Примеры таких показателей - минимальный и максимальный элементы выборки (первый и последний члены вариационного ряда), верхний и нижний квартили (ограничивают зону, в которую попадают 50% центральных элементов выборки). Наконец, сведения о середине совокупности могут дать средняя арифметическая, средняя гармоническая, медиана и другие характеристики.

2. Показатели разброса описывают степень разброса данных относительно своего центра. К ним в первую очередь относятся: дисперсия, стандартное отклонение, размах выборки (разность между максимальным и минимальным элементами), межквартильный размах (разность между верхней и нижней квартилью), эксцесс и т. п. Эти показатели определяют, насколько кучно основная масса данных группируется около центра.

3. Показатели асимметрии характеризуют симметрию распределения данных около своего центра. К ним можно отнести коэффициент асимметрии, положение медианы относительно среднего и т. п.

4. Показатели, описывающие закон распределения, дают представление о законе распределения данных. Сюда относятся таблицы частот, таблицы частостей, полигоны, кумуляты, гистограммы (см. раздел 2).

На практике чаще всего используются следующие показатели: средняя арифметическая, медиана, дисперсия, стандартное отклонение. Однако для получения более точных и достоверных выводов необходимо учитывать и другие из перечисленных выше характеристик, а также обращать внимание на условия получения выборочных совокупностей. Наличие выбросов, т. е. грубых ошибочных наблюдений, может не только сильно исказить значения выборочных показателей (выборочного среднего, дисперсии, стандартного отклонения и т. д.), но и привести ко многим другим ошибочным выводам.

Наиболее распространенной формой статистических показателей, используемой в социально – экономических явлениях, является средняя величина, представляющая собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.

Сущность средней состоит в том, что в ней взаимопогащаются отклонения значений признака у отдельных единиц совокупности, обусловленные действием случайных факторов. Наиболее распространенным видом средних величин является средняя арифметическая, которая как и все средние, в зависимости от характера имеющихся данных может быть простой или взвешенной.

Средняя арифметическая простая ( не взвешенная). Эта форма средней используется в тех случаях, когда расчет осуществляется по не сгруппированным данным. Зависимость для определения простой средней арифметической имеет вид:



Средняя арифметическая взвешенная. При расчете средних величин отдельные значения осредняемого признака могут повторяться (встречаться по несколько раз). В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам Зависимость для определения средней арифметической взвешенной для дискретного вариационного ряда имеет вид:

, где f_i – частота i-го признака

Наряду со средней арифметической, в санитарной статистике применяются, хотя и реже, такие виды средних, как медиана и мода.

Медиана (обозначаемая буквами Ме) — это серединная, центральная варианта, делящая вариационный ряд пополам, на две равные части.

Мода (обозначаемая Мо) — чаще всего встречающаяся или наиболее часто повторяющаяся величина, соответствующая при графическом изображении максимальной ординате, т. е. наивысшей точке графической кривой. Таким образом, при приближенном нахождении моды в простом (несгруппированном) ряду она определяется как наиболее насыщенная или частая величина, как варианта с наибольшим количеством частот.

Средняя арифметическая (М) является результативной суммой всех влияний. В ее формировании принимают участие все без исключения варианты, в том числе и крайние варианты. Медиана и мода, в отличие от средней арифметической, не зависят от величины всех индивидуальных значений, т. е. всех членов вариационного ряда, а обусловливаются относительным расположением или распределением вариант. Поэтому медиану и моду также называют описательными или позиционными средними, т. к. они характеризуют главнейшие свойства данного распределения. Особенно это касается медианы, являющейся в известном смысле, непараметрической величиной. М характеризует всю массу наблюдений, а Ме и Мо — основную массу, без учета воздействия крайних вариант, т. е. исключая крайние значения, зависящие иногда от случайных причин.

Средние арифметические величины, взятые сами по себе без дополнительных приемов оценки, имеют подчас ограниченное значение, т. к. они не отражают степени разброса (или рассеяния) ряда.

Одинаковые по размеру средние могут быть получены из рядов с различной степенью рассеяния. Средние — это величины, вокруг которых рассеяны различные варианты. Понятно, что чем ближе друг к другу отдельные варианты, (значит меньше рассеяние, колеблемость ряда), тем типичнее его средняя.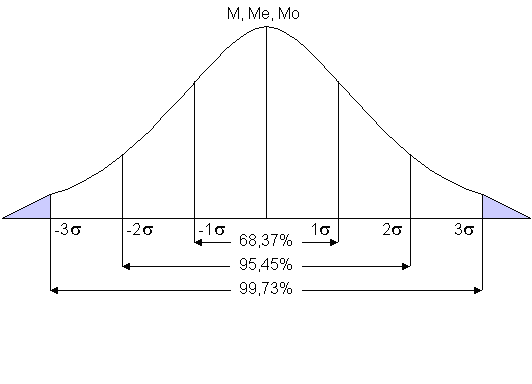


Рис. 12 Средние величины в ряду с нормальным распределением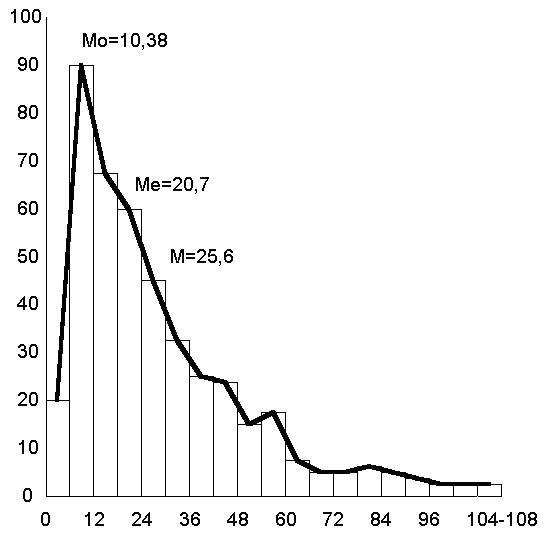


Рис. 13 Средние величины в ряду с ассиметричным распределением

Меры разброса (рассеяния). Средние арифметические величины, взятые сами по себе без дополнительных приемов оценки, имеют подчас ограниченное значение, т. к. они не отражают степени разброса (или рассеяния) ряда.

Одинаковые по размеру средние могут быть получены из рядов с различной степенью рассеяния. Средние — это величины, вокруг которых рассеяны различные варианты. Понятно, что чем ближе друг к другу отдельные варианты, (значит меньше рассеяние, колеблемость ряда), тем типичнее его средняя. Существует ряд показателей, с помощью которых как раз и оценивается мера разброса или рассеяния ряда.

Размах – разность между наибольшими и наименьшими значениями в ряде или распределении. Размах учитывает только экстремальные значения и поэтому не дает информации о разбросе отдельных элементов

Дисперсия – средний квадрат отклонения значений от их арифметического среднего

Среднеквадратичное отклонение – положительный корень из дисперсии. Это показатель разброса данных около арифметического среднего

Коэффициент вариации – это среднеквадратичное отклонение, деленное на арифметическое среднее, выраженное в процентах.