Рабочая тетрадь теория отраслевых рынков. Рабочая тетрадь Теория отраслевых рынков. Рабочая тетрадь дисциплины теория отраслевых рынков
 Скачать 399.3 Kb. Скачать 399.3 Kb.
|
Вопрос 2. Взаимосвязь структуры рынка и расходов на рекламуРеклама способствует формированию сильного имиджа товарной марки и установлению монопольной власти. Структура рынка также может воздействовать на уровень рекламных расходов и расходов на методы стимулирования сбыта. Вероятнее всего, расходы на рекламу в свою очередь также оказывают воздействия на структуру рынка. Общая проблема изучения уровня расходов на рекламу и других расходов по стимулированию сбыта, максимизирующих прибыли фирм, должна рассматриваться в условиях функционирования олигополистического рынка. Таким образом, максимизирующая прибыль доля расходов на рекламу в объеме продаж тем больше, чем больше равновесная разница между ценой и предельными издержками и чем более чувствителен спрос к росту расходов на рекламу. В условиях совершенной конкуренции предельные издержки равны цене и поэтому расходы на рекламу оказываются нулевыми. Действительно, в условиях свободной конкуренции продавец не ограничен в объеме продаж своего товара по установленной рынком цене. Поэтому нет никакой необходимости тратить средства на рекламу. При этом доля расходов на рекламу в объеме продаж должна увеличиваться по мере того, как рынок трансформируется из конкурентной структуры в олигопольную или монопольную. Если олигополисты могут увеличить долю рынка по сравнению с конкурентами средством рекламы (индекс HHI), то взаимосвязь между долей расходов на рекламу в объеме продаж и уровнем концентрации существует. Особого внимания требует изучение максимального значения рекламных расходов в отрасли в зависимости от структурных характеристик рынка. Для подтверждения многих гипотез, которые здесь уместны, большое значение имеет анализ качественных данных эмпирической реальности. Сложность анализа данной проблемы обусловлена разнообразием структурных и поведенческих предпосылок. Такими предпосылками могут быть монополия, входные барьеры, торможение вхождения в отрасль посредством ценообразования и инвестиционной политики, предопределяющей разнообразие продуктов, неограниченная неценовая олигопольная конкуренция в условиях сговора, конкуренция между фирмами, которые по-разному воспринимают взаимозависимость в отношении цены и качества товара (например, монополистическая конкуренция и жесткая гомогенная олигополия). Нельзя исключать из рассмотрения и правительственные меры, по созданию различного рода ограничений в отношении уровня концентрации в отрасли, повышения цены и требований к качеству продукции. Пример решения типовых задач Задание 1. Предприятие работает в условиях совершенной конкуренции. Выпуск продукции за некоторый период времени и общие издержки предприятия представлены в таблице:
Определите оптимальный объем выпуска для данного предприятия, если цена товара на рынке установилась на уровне 125000 руб. Решение: В условиях совершенной конкуренции объем выпуска, максимизирующий прибыль фирмы, будет выбран при условии р = МС. Найдем предельные издержки МС.
Предприятие будет выпускать 8 единиц, т.к. при данном объеме выпуска р = МС = 125 тыс. руб. Задача 2. Расчёт оптимального выпуска и цены до и после рекламной кампании. Функция полных затрат фирмы — монополистического конкурента на своем узком рынке: ТС = 3×Q2 – 8. Рыночный спрос на продукцию фирмы: Р = 64 – Q. После проведения рекламной кампании, затраты на которую составили Срекл= 6×Q – 10, остаточный спрос увеличился и составил Р = 76 – 2×Q. Определите оптимальный выпуск и цену, которые установит фирма на свою продукцию до и после рекламной кампании. Дайте характеристику эффективности рекламы в данном случае. Решение: В точке оптимума фирмы, работающей в условиях монополистической конкуренции, выполняется равенство предельных издержек и предельной выручки: МС = MR. До рекламной кампании выручка фирмы была равна: TR = Q × P = 64 × Q – Q2 Найдём функцию предельной выручки: MR = (TR)' = 64 – 2 × Q. Продифференцировав функцию общих издержек, найдём функцию предельных издержек: MC = (TC)' = (3 × Q2 – 8)' = 6Q Так как МС = MR 6Q = 64 – 2Q 8Q = 64 Q = 8 – оптимальный выпуск фирмы P = 64 – 8 = 56 – оптимальная цена. При этом прибыль фирмы составила: П = TR – ТС = Q × P – ТС = 8 × 56 – 3 × 82 + 8 = 264 После проведения рекламной кампании выручка фирмы стала равна: TR = Q × P = Q × (76 – 2 × Q) = 76 × Q – 2 × Q2 MR = 76 – 4 × Q Функция предельных затрат стала иметь следующий вид: TC = 3 × Q2 – 8 + 6 × Q – 10 = 3 × Q2 + 6 × Q - 18 MC = 6 × Q + 6 Найдём оптимум фирмы после проведения рекламной кампании: MR = MC 76 – 4 × Q = 6 × Q + 6 10 × Q = 70 Q = 7 P = 76 - 2 × 7 = 62 После рекламы прибыль фирмы стала равна: П = TR – ТС = Q × P – ТС = 7 × 62 – (3 × 72 + 6 × 7 – 18) = 263 Как видно после проведения рекламной кампании прибыль фирмы уменьшилась, следовательно, рекламная кампания оказалась не эффективна. Задача 2. Расчёт объема выпуска продукции На рынке цена продукции установилась на уровне 6 денежных единиц. Известны следующие показатели деятельности фирмы, работающей на конкурентном рынке.
Определить двумя способами объём выпуска продукции, при котором прибыль фирмы будет максимальной: 1. Сопоставляя общую выручку и общие издержки. 2. Сопоставляя предельный доход и предельные издержки. Привести расчетные формулы, заполнить таблицу. Решение: 1. Найдём общую выручку по формуле: TR = Q × P Результаты вычислений занесём в таблицу.
Сопоставив общую выручку и общие издержки, приходим к выводу, что прибыль П = TR - TC будет максимальной (графа 4) при двух значениях объёма выпуска: Q = 2 и Q = 3, следовательно, они одинаково оптимальны с точки зрения фирмы. 2. В условиях совершенной конкуренции предельный доход равен цене: MR = P = 6 при любом объёме выпуска. Фирма, максимизирующая прибыль, выберет такой объём производства, при котором предельные затраты будут равны предельному доходу. То есть выполняется равенство: MС = MR. Или предельная прибыль будет равна нулю. Предельные затраты (МС) – это прирост общих затрат, связанный с ростом выпуска продукции на дополнительную единицу. 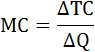 Предельная прибыль (Мπ) – это прирост общей прибыли, связанный с производством дополнительной единицы продукции. 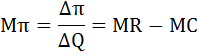 Итак, правило принятия решения об объёме производства будет следующим: пока предельная прибыль положительна, предприятию следует наращивать объём производства. Рассчитаем величину предельных затрат и предельной прибыли результаты занесём в таблицу. Как видно из таблицы предельная прибыль равна нулю при Q=3. Следовательно, объем выпуска продукции, при котором прибыль фирмы будет максимальной равен 3. Примерный перечень типовых задач: Задание 1. Предприятие работает в условиях совершенной конкуренции. Выпуск продукции за некоторый период времени и общие издержки предприятия представлены в таблице:
Определите оптимальный объем выпуска для данного предприятия, если цена товара на рынке установилась на уровне 125000 руб. Задание 2. Функция полных затрат фирмы — монополистического конкурента на своем узком рынке: ТС = 3×Q2 – 8. Рыночный спрос на продукцию фирмы:Р = 64 – Q. После проведения рекламной кампании, затраты на которую составилиСрекл= 6×Q – 10, остаточный спрос увеличился и составилР = 76 – 2×Q. Определите оптимальный выпуск и цену, которые установит фирма на свою продукцию до и после рекламной кампании. Дайте характеристику эффективности рекламы в данном случае. Задание 3.На рынке цена продукции установилась на уровне 6 денежных единиц. Известны следующие показатели деятельности фирмы, работающей на конкурентном рынке.
Определить двумя способами объём выпуска продукции, при котором прибыль фирмы будет максимальной: 1. Сопоставляя общую выручку и общие издержки. 2. Сопоставляя предельный доход и предельные издержки. Привести расчетные формулы, заполнить таблицу. Задание 4.Зависимость общих затрат предприятия (ТС) от выпуска представлена в таблице:
На рынке цена установилась на уровне 110 р. а) Сколько продукции должно производить предприятие, чтобы достичь максимума прибыли? б) Не следует ли прекратить производство? в) Ниже какого уровня должна снизиться цена, чтобы предприятие прекратило производство данного товара? Задание 5.Сто фирм в условиях совершенной конкуренции имеют следующую зависимость общих издержек от объёма выпуска:
а) Определите рыночную цену. б) Является ли производство прибыльным? Какую экономическую прибыль (убыток) получает одна фирма? Задание 6.В отрасли совершенной конкуренции установилась цена Р = 30. В эту отрасль входит фирма с общими издержками ТС = 1/2 * Q2 + 10 * Q + 100. Найти её объём производства в краткосрочном периоде. Задание 7.Функция издержек фирмы ТС = Q2 - Q + 3, где Q - объём производства. Рыночная цена на продукцию фирмы составляет 7 и не зависит от объёма продаж этой фирмы. Найти объём выпуска продукции, максимизирующий прибыль фирмы. Задание 8.Общие затраты фирмы, действующей на рынке совершенной конкуренции, составляют 0,5*Q3 - 15*Q2 + 300*Q + 250 000. При какой цене фирме становится невыгодным работать на этом рынке в краткосрочном периоде? Задание 9.Конкурентная фирма находится в состоянии равновесия в долгосрочном периоде и имеет следующие затраты: TC = Q3 - 38*Q2+ 418*Q. Определите цену на этом рынке в долгосрочном периоде. Задание 10.Функция издержек конкурентной фирмы ТС = Q3 – 20*Q2 + X*Q + 8000, где Q – объём производства в тысячах единиц.Известно, что при цене, равной 20, фирме выгодно покинуть отрасль в краткосрочном периоде, а при цене 50 – выгодно остаться в отрасли.Найти допустимый интервал значений Х. Задание 11.В отрасли действуют 130 одинаковых фирм. Издержки производства каждой фирмы описываются функциями ТС =Q3 - 36*Q2 + 384*Q,гдеQ - объём производства в тысячах штук. Найти рыночную цену и отраслевой выпуск продукции, при которых на конкурентном рынке устанавливается долгосрочное равновесие. Задание 12.Фирма, находясь в условиях совершенной конкуренции, имеет следующую функцию общих затрат:ТС = 140 + 10 × Q + 40 × Q2.При каком выпуске прибыль фирмы достигнет максимума, если цена установилась на уровне 250 ден. ед.? Определить размер прибыли фирмы. Будут ли в длительном периоде в эту отрасль стремиться войти новые фирмы? Задание 13.Конкурентная фирма имеет общие затраты ТС = 800 + 40*Q + 2*Q2 Она получает в краткосрочном периоде максимально возможную прибыль, равную 1000. Определить цену на рынке и объём выпуска данной фирмы. Задание 14.Спрос на продукцию конкурентной отрасли: Qd = 55 – P; Предложение: Qs = 2P – 5 Если у одной из фирм отрасли восходящий участок кривой предельных издержек: МС = 3Q + 5 При каких цене и объёме производства фирма максимизирует прибыль? Задание 15.В краткосрочном периоде у менеджеров конкурентной фирмы имеются следующие данные (каждый набор данных а), б) и так далее следует рассматривать отдельно): а) TR = 160, VC = 3, AVC = 0,15, МС = 7. б) TR = 9000, VC = 2000, FC = 4000, AC = 2, МС = 3,1. в) Q = 200, TR = 8000, AVC = 43, MC = 40. г) Q = 500, TC = 30000, P = 60, MC = AC. д) MC = 20, P = 20, VC = 1500, FC = 1000, AC = 25. Какой вариант поведения фирмы следует выбрать из нижеперечисленных на основании анализа этих показателей? 1. Прекратить производство. 2. Оставить всё как есть. 3. Сократить объём выпуска. 4. Увеличить объём выпуска. Задание 16.Функция общих затрат монополии имеет вид ТС = 200 + 30Q,функция спроса на её продукцию Р = 60 - 0,2Q.Определить цену, при которой фирма максимизирует прибыль. Задание 17.Найти максимум прибыли монополиста, если известно, что спрос на его продукцию описывается функцией: Q = 165 - 0,5 × Pи функция общих затрат равна:TC = 5500 + 30 × Q + Q2 Задание 18.Постоянные затраты монополиста составляют 180 тыс. р. Средние переменные затраты постоянны и равны 20 р. Функция спроса задана уравнением Qd = 500 - 0,5 × Р, где Р - цена в рублях, Q - количество в тысячах штук. Найти Qm и Pm - объём продаж и цену, максимизирующие прибыль монополиста. Задание 19.Монополия максимизирует выручку при целевой прибыли не ниже 1500 единиц. Известны функция спросаP = 304 - 2 × Qи функция затратТС = 500 + 4 × Q + 8 × Q2 а) Определить оптимальный объём выпуска и цену. б) Какими были бы оптимальный выпуск и цена, если бы монополия преследовала цель максимизации прибыли? Задание 20.У монополистически конкурентной фирмы известна функция цены: P = 1000 – 10 × Q и функция совокупных издержек:TC = 100 + 5 × Q. 1. Определите оптимальный объём выпуска и цену товара у этой фирмы. Чему равна её экономическая прибыль?2. Если бы данный сегмент рынка был совершенно конкурентным, то сколько продукции производилось бы и по какой цене она бы продавалась? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
