№
| Темы практических занятий |
Объем часов занятия
|
|
I СЕМЕСТР
|
|
1
|
Метод математической индукции. Операции над множиствами. Границы числовых множеств.
|
2
|
|
Последовательность чисел и их предел.
|
|
2
|
Примеры на ограниченные, неограниченные и монотонные последовательности. Вычисление предела последовательности с помощью определения. Вычисление предела последовательности.
|
2
|
3
|
Исследование сходимоси последовательностей
|
2
|
4
|
Нахождение нижнего и верхнего предела последовательности.
|
2
|
|
Функйия
|
|
5
|
Область определения, ограниченность, чётность и периодичность функции. График сложной функции.
|
2
|
|
Предела функций и непрерывность
|
|
6
|
Вычисление предела функции с помощью определения.
|
2
|
7
|
Примеры нахождения предела функции. Правые и левые пределы.
|
2
|
8
|
Исследование непрерывности функции с помощью определения.
|
2
|
9
|
Примеры нахождения точек разрыва функции.
|
2
|
10
|
Примеры на свойства непрерывных функции. Исследование непрерывности сложной функции и её график.
|
2
|
11
|
Исследование равомерной непрерывности функции с помощью определения.
|
2
|
12
|
Исследованиеравномерную непрерывность с помощью теоремы Кантора.
|
2
|
|
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ
|
|
13
|
Вычисление производной функции с помощью определения. Примеры на вычисление производной.
|
2
|
14
|
Примеры на геометрический смысл производной функции. Исследование дифференцируемости функции. Вычисление дифференциала функции. Примеры на приближенное вычисление.
|
2
|
15
|
Примеры производные и дифференциалы высших порядков. Примеры основных теорем дифференциального вычисления.
|
2
|
16
|
Примеры формулы Тейлора
|
2
|
17
|
Исследование монотонности функции с помощью производной. Доказательство неравенств с помощью производной.
|
2
|
18
|
Нахождение экстремальных значений функции.
|
2
|
19
|
Примеры выпуклость и вогнутость функции. Исследование функций. Правила Лопиталя.
|
2
|
|
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
|
|
20
|
Примеры для вычисления неопределенного интеграла. Метод замены переменной. Метод интегрирования по частям.
|
2
|
21
|
Метод интегрирования по частям.
|
2
|
22
|
Примеры на интегрирование рациональных функций.
|
2
|
23
|
Примеры на интегрирование тригонаметрических и некоторых иррациональных функций.
|
2
|
|
Итого:
|
46
|
|
II СЕМЕСТР
|
|
|
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
|
|
24
|
Вычисление определенного интеграла по определению. Примеры к вычислению определенного интеграла.
|
2
|
25
|
Вычисление предела с помощью определенного интеграла. Оценивание определенного интеграла.
|
2
|
26
|
Примеры на применения определенного интеграла.
|
2
|
|
НЕСОБСТВЕННЫЙ ИНТЕГРАЛ
|
|
27
|
Примеры к вычислению несобственного интеграла первого рода.
|
2
|
28
|
Несобственный интеграл первого рода и её сходимость.
|
2
|
29
|
Вычисление несобственный интеграл второго рода.
|
2
|
30
|
Примеры к исследование сходимость несобственных интегралов второго рода.
|
2
|
|
ПРОСТРАНСТВО Rn
|
|
31
|
Вычисление предела последовательности в пространстве 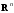 . Примеры на нахождение области определения функции нескольких переменных. . Примеры на нахождение области определения функции нескольких переменных.
|
2
|
32
|
Вычисление повторной и кратной пределов функции нескольких переменных.
|
2
|
33
|
Примеры на непрерывность и разрыв функции нескольких переменных. Исследование равомерной непрерывности функции нескольких переменных.
|
2
|
|
ЧАСТНЫЕ ПРОИЗВОДНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.
|
|
34
|
Примеры на нахождение частной производной функции нескольких переменных.
|
2
|
35
|
Исследование на дифференцируемость функции нескольких переменных. и её вычисление. Производная сложной функции.
|
2
|
36
|
Производная и дифференциал высших порядков для функции нескольких переменных.
|
2
|
37
|
Формула Тейлора функции нескольких переменных.
|
2
|
38
|
Исследование экстремум функции нескольких переменных
|
2
|
39
|
Нахождение производной неявной функции.
|
2
|
|
ЧИСЛОВЫЕ РЯДЫ
|
|
40
|
Примеры, относящиеся вычислению числовых рядов. Примеры относящиеся сходимости и расходимости числового ряда.
|
2
|
41
|
Признаки сходимости рядов с положительными членами (признак Коши, признак Даламбера интегралный признак, признак сравнения признак Раабе, признак Гаусса).
|
2
|
42
|
Примеры ,относящиеся рядам с произвольными членами и признакам сходимости Лейбница, Дирихле и Абеля.
|
2
|
|
ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ.
|
|
43
|
Исследование на равномерную сходимость функциональных последовательностей. Нахождение области сходимости функционального ряда.
|
2
|
44
|
Исследование на равномерную сходимость функциональных рядов (признак Вейерштрасса, признаки Абеля и Дирихле, критерия Коши).
|
2
|
45
|
Примеры, относящиеся почленному переходу к пределу, непрерывности суммы ряда, почленному дифференцированию и интегрированию функционального ряда.
|
2
|
|
Итого_:__44___I_II__СЕМЕСТР'>Итого:
|
44
|
|
III СЕМЕСТР
|
|
|
СТЕПЕННЫЕ РЯДЫ.
|
|
46
|
Нахождения области сходимости и радиуса сходимости степенного ряда.
|
2
|
47
|
Нахождение суммы степенного ряда.
|
2
|
48
|
Разложение функции в степенной ряд. Разложение функции ряда Фурье.
|
2
|
|
РЯДЫ ФУРЕ
|
|
49
|
Разложение функции по интервалам 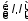 ряда Фурье. ряда Фурье.
|
2
|
50
|
Разложение функции по интервалам 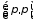 ряда Фурье. Разложение функции не симметрично интервале ряда Фурье. ряда Фурье. Разложение функции не симметрично интервале ряда Фурье.
|
2
|
51
|
Сходимость ряда Фурье
|
2
|
|
КРАТНЫЕ ИНТЕГРАЛЫ
|
|
52
|
Вычисление кратные интегралы с помощью определения.
|
2
|
53
|
Примеры, относящиеся изменению порядка интегрирования.
|
2
|
54
|
Вычисление двухкратного интеграла
|
2
|
55
|
Замена переменной при вычислении двухкратного интеграла
.
|
2
|
56
|
Примеры применения двойных интегралов.
|
2
|
57
|
Тройной интеграл.
|
2
|
|
КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
|
|
58
|
Вычисление криволинейного интеграла первого рода.
|
2
|
59
|
Вычисление криволинейного интеграла второго рода
|
2
|
60
|
Примеры к применению формулы Грина
|
2
|
|
Итого:
|
30
|
|
Всего часов
|
120
|
 Скачать 67.12 Kb.
Скачать 67.12 Kb.
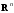 . Примеры на нахождение области определения функции нескольких переменных.
. Примеры на нахождение области определения функции нескольких переменных.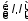 ряда Фурье.
ряда Фурье.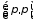 ряда Фурье. Разложение функции не симметрично интервале ряда Фурье.
ряда Фурье. Разложение функции не симметрично интервале ряда Фурье.