РТЦиС_метода к лабам. Радиотехнические цепи и сигналы лабораторный практикум
 Скачать 1.84 Mb.
|
3.2. Описание лабораторной установкиЛабораторная установка состоит из отдельного макета и двух осциллографов С1–83 (I) и С1–83 (II). В отдельном макете находятся генератор исследуемых случайных сигналов, а также измерители функции распределения вероятностей и плотности распределения вероятностей. Структурная схема макета установки (рис. 3.9) изображена на его передней панели. 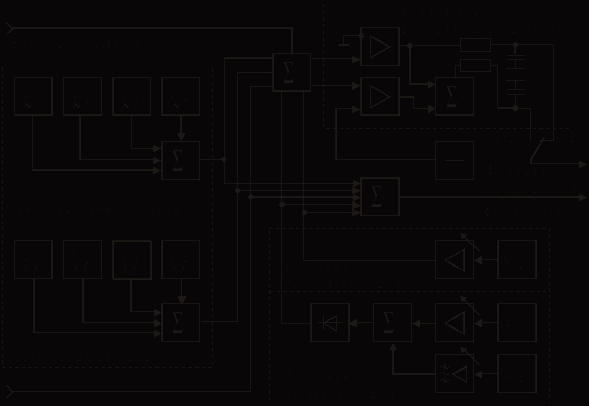 Рис. 3.9 С выхода «  » осциллографа С1–83 (I) снимается в качестве опорного пилообразное напряжение горизонтальной развертки и подается в лабораторный макет на «Вход U» для использования в качестве аргумента «U» функции распределения.Выход «Функция распределения» установки соединяется с входом «» осциллографа С1–83 (I). На экране осциллографа появляется изображение функции распределения F(U) или плотности распределения вероятностей p(U). Выбор зависит от положения переключателя «F(U) — p(U)» на передней панели экспериментальной установки. Выход «Форма сигнала» установки соединяется со входом «» осциллографа С1–83 (II), на экране которого наблюдают изображение исследуемого сигнала. В макете установки имеются следующие источники сигналов:
Имеется также вход для внешнего сигнала. Выходы всех источников сигналов подключены через сумматор ко входу измерителя функций распределения. Каждый источник сигнала имеет тумблер включения и регулировку уровня (только часть регуляторов уровня выведена на переднюю панель). 3.3. Задание и указания к выполнению работы1. Подготовить установку к измерениям. На осциллографе С1–83 (I) установить коэффициент развертки 0,1 с/дел, коэффициент отклонения 0,2 В/дел. Включить осциллографы и экспериментальную установку. В установке выключить все генераторы (ручки тумблеров — вниз), что соответствует нулевому сигналу на входе измерителя функции распределения; тумблер «Функции распределения» — в положении F(U). На экране С1–83 (I) появится изображение ступенчатой функции  Регулировкой смещения и коэффициента отклонения осциллографа установить изображение так, чтобы скачок находился в центре экрана и величина скачка была равна 3–4 см. 2. Откалибровать изображение на экране С1–83 (I). Включить генератор треугольного сигнала № 4 (ручка тумблера — вверх). На экране С1 83 (I) переход от F(U) = 0 к F(U) = 1 будет иметь вид наклонной линии (см. рис. 3.3, в). Точки излома соответствуют минимальному  и максимальному  значениям треугольного сигнала. Измерить расстояние по горизонтали между точками излома — L, дел. На экране осциллографа С1 83 (II) получить изображение треугольного сигнала (см. рис. 3.3, а) и измерить его размах  , В. Масштаб по горизонтали для изображения на экране осциллографа С1–83 (I) равен  , В/дел. Данный масштаб является одинаковым для всех получаемых в дальнейшем графиков функций распределения F(U) и плотностей вероятности p(U).Переключатель «Функции распределения» в установке перевести в положение «p(U)». На экране С1–83 (I) появится П-образное изображение, соответствующее равномерному распределению вероятности, характерному для треугольного сигнала (см. рис. 3.3, б). Если изображение по вертикали занимает L делений, то масштаб изображения p(U) по вертикали составит  , (Вдел)–1. Данный масштаб является одинаковым для всех получаемых в дальнейшем графиков плотностей вероятности p(U).Определять вертикальный масштаб для графиков функций распределения нет необходимости — он очевиден благодаря предельным свойствам функций распределения (  и  ).В дальнейшем коэффициент отклонения осциллографа C1–83 (I) не изменять. 3. Исследовать функции распределения и плотности вероятностей мгновенных значений для следующих сигналов:
Указанные варьируемые параметры выбрать самостоятельно таким образом, чтобы на графиках было хорошо заметно их влияние на форму функции распределения и плотности вероятности. Исследование производится следующим образом. В исходном положении все генераторы выключены. Включить генератор исследуемого сигнала. По изображению сигнала на экране С1–83 (II) убедиться, что включен требуемый сигнал. По изображению на экране С1–83 (II) или по вольтметру, подключенному к выходу «Форма сигнала» установки (параллельно входу осциллографа), определить диапазон регулировки уровня исследуемого сигнала (амплитуда для гармонического и треугольного, эффективное значение для шумов). В этом диапазоне выбрать два значения уровня исследуемого сигнала и для каждого из них зарисовать с экрана С1–83 (I) изображения функций p(U) и F(U) с учетом ранее определенных масштабов по осям. 4. Исследовать сходимость к гауссовскому закону распределения суммы независимых случайных сигналов. Выяснить, для какого из двух исходных законов распределения — равномерного (треугольный сигнал) или вида  (гармонический сигнал) — характерна более быстрая сходимость.Для суммы гармонических сигналов исследование производится следующим образом. В исходном положении все генераторы выключены. Включить генератор синусоидального сигнала № 1 и зарисовать график функции распределения F(U). Затем, не выключая генератор этого сигнала, включить генератор синусоидального сигнала № 2 и зарисовать график функции распределения F(U) для суммы двух синусоидальных сигналов. Далее поочередно дополнительно включить генераторы синусоидальных сигналов № 3 и № 4, каждый раз зарисовывая графики функции распределения суммарного сигнала. Для суммы треугольных сигналов исследование производится аналогичным образом. |