РТЦиС_метода к лабам. Радиотехнические цепи и сигналы лабораторный практикум

• Название: Радиотехнические цепи и сигналы лабораторный практикум
• Анкор: РТЦиС_метода к лабам.doc
• Дата: 26.12.2017
• Размер: 1.84 Mb.
• Имя файла: РТЦиС_метода к лабам.doc
• Тип: Практикум; #13019
• страница: 7 из 25

Содержание отчета

Отчет по работе должен включать в себя следующее:

• 
  результаты определения масштабов графиков согласно п. 2;
  
• 
  графики функций распределения и плотностей вероятностей значений сигналов, исследованных в п. 3.
  
• 
  анализ соответствия графиков, полученных в п. 3, теоретическим результатам (выражения (3.3)–(3.7)) 4;
  
• 
  графики функций распределения для последовательных сумм синусоидальных и треугольных сигналов согласно п. 4;
  
• 
  вывод о скорости сходимости распределения вероятности суммы независимых случайных сигналов к гауссовскому закону.
  

Контрольные вопросы

1. 
   Как измеряют функцию распределения по одной реализации эргодического случайного процесса?
   
2. 
   Определить функцию распределения F(x), математическое ожидание m_x и дисперсию D_x для случайной величины, имеющей заданную преподавателем плотность вероятности p(x).
   
3. 
   Определить плотность вероятности p(x), математическое ожидание m_x и дисперсию D_x для случайной величины, имеющей заданную преподавателем функцию распределения F(x).
   
4. 
   Могут ли эти функции быть функциями распределения вероятности?
   

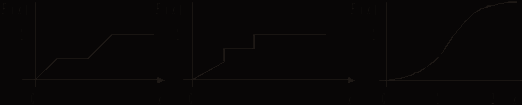
а б в

5. 
   Могут ли эти функции быть функциями плотности вероятности?
   

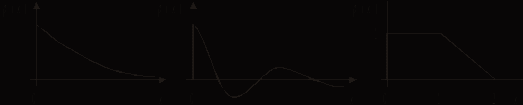
а б в

6. 
   Как зависит плотность вероятности нормального закона от входящих в нее параметров? Пояснить графически.
   
7. 
   Как зависит плотность вероятности обобщенного закона Рэлея от параметров и ?
   
8. 
   Плотность распределения случайного сигнала u(t) представлена суммой
   

.

Записать и построить функцию распределения F(u) и определить математическое ожидание и дисперсию u(t). Привести пример реализации u(t).

9. 
   Известно, что плотность распределения суммы двух независимых случайных сигналов u(t) и v(t) с плотностями распределения и является сверткой
   

.

Рассчитать для заданной преподавателем суммы двух сигналов, исследованных в работе, и сравнить с экспериментальными данными.

10. 
    Случайная величина  принимает значения /4 и –/4 с вероятностями 0,5. Найти ковариационную функцию случайного процесса x(t) = sin(₀t + ). Является ли данный процесс стационарным?
    
11. 
    Случайный процесс x_i(t) = 2sin(₀t + _i), где {_i} — набор статистически независимых случайных величин, равномерно распределенных в диапазоне от – до . Найти плотность вероятности случайного процесса .
    
12. 
    Может ли функция распределения вероятности:
    

а) принимать постоянное значение на некотором интервале?

б) иметь скачок в некоторой точке?

Если может, то что можно сказать о данном интервале (точке)?
4. ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК
ЧАСТОТНО-ИЗБИРАТЕЛЬНЫХ ЦЕПЕЙ
НА ОСНОВЕ КОЛЕБАТЕЛЬНЫХ КОНТУРОВ
Цель работы — изучение частотно-избирательных цепей на основе колебательных контуров. Последовательный и параллельный колебательные контуры часто используются в качестве основного элемента линейных частотно-избирательных цепей (фильтров, резонансных усилителей и т. п.). К основным характеристикам линейных цепей относятся импульсная характеристика h(t)и комплексный коэффициент передачи (частотная характеристика) . В исследуемых цепях вид этих характеристик полностью определяется резонансной частотой и добротностью Q контуров, а связь между ними — преобразованиями Фурье.

Исследуются временные и частотные характеристики колебательных контуров, влияние на них активных потерь, взаимосвязь временных и частотных параметров контуров.