Документ Microsoft Word. Размах вариации r

• Название: Размах вариации r
• Дата: 11.09.2022
• Размер: 85.75 Kb.
• Имя файла: Документ Microsoft Word.docx
• Тип: Документы; #671566
• страница: 2 из 3

Понятие о выборочном наблюдении

Выборочное наблюдение представляет собой такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, далее отобранная часть изучается, а затем результаты распространяются на всю исходную совокупность. Наблюдение осуществляется таким образом, что эта часть отобранных единиц представляет всю совокупность с достаточной для практике степенью точности.

Совокупность, из которой производится отбор, называется генеральной,и все ее обобщающие показатели – генеральными.

Выборочная совокупность –это совокупность единиц, отобранных из генеральной совокупности. Все ее обобщающие показатели называются выборочными.

Основными причинами, по которым во многих случаях выборочному наблюдению отдается предпочтение перед сплошным, являются:

1. 
   экономия материальных, трудовых, финансовых ресурсов и времени в результате сокращения объема работы;
   
2. 
   сведения к минимуму порчи или уничтожения исследуемых объектов;
   
3. 
   необходимость детального исследования каждой единицы наблюдения при невозможности охвата всех единиц (например, при изучении бюджета домохозяйств);
   
4. 
   достижение достаточно большой точности результатов обследования благодаря сокращению ошибок, происходящих при регистрации.
   

Преимущество выборочного наблюдения по сравнению со сплошным можно реализовать, если оно организовано и приведено в соответствии с научными принципами теории выборочного метода. Это обеспечение случайности, т. е. равной возможности попадания в выборку единиц генеральной совокупности, и достаточного числа единиц отбора.

Основная задача выборочного наблюдения состоит в том, чтобы на основе характеристик выборочной совокупности (т.е. средней и доли) получить достоверные суждения о показателях средней и доли в генеральной совокупности. При этом следует иметь в виду, что при любых статистических исследованиях (сплошных и выборочных) возникают ошибки.

Ошибки регистрации могут возникать и при сплошных, и при выборочных наблюдениях. Они могут иметь случайный (непреднамеренный) и систематический (преднамеренный) характер.

Ошибки репрезентативности (представительности) присущи только выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную. Они представляют собой расхождение между значениями показателей, полученных по выборке, и значениями показателей этих же величин, которые были бы получены при проведенной с одинаковой степенью точности сплошном наблюдении, т.е. между величинами выборочных и генеральных характеристик.

Ошибки репрезентативности возникают вследствие двух причин:

1) из-за нарушения принципа случайности как основного принципа выборки (систематические ошибки)

2) в результате самого отбора (случайные ошибки)

Систематические ошибки выборки устраняются. Случайные ошибки устранить нельзя, но их рассчитывают и учитывают при переносе выборочных характеристик на генеральную совокупность.

Случайные ошибки репрезентативности бывают средними (   ) и предельными (   ) .

Средняя ошибка выборки представляет собой такое расхождение между средними выборочной и генеральной совокупностей, которое не превышает среднеквадратическое отклонение в выборке.

Предельной ошибкой называется максимальное расхождение средних характеристик выборочной и генеральной совокупностей при заданной вероятности появления этой ошибки.

По методу отбора различают повторную и бесповторную выборки.

При повторной выборке ту или иную единицу, попавшую в выборку, после регистрации снова возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами вновь попасть в выборку.

При бесповторной выборке единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшем в выборке не участвует.

По степени охвата единиц совокупности различают большие и малые (n < 30) выборки.

В практике выборочных исследований наибольшее распространение получили следующие виды выборки: простая случайная (собственно - случайная), механическая, типическая, серийная, комбинированная и др.

Основные характеристики параметров генеральной и выборочной совокупности обозначаются символами:

N – объем генеральной совокупности (количество единиц, входящих в генеральную совокупность)

n – объем выборочной совокупности (количество единиц, входящих в выборочную совокупность )

 - генеральная средняя (среднее значение признака в генеральной совокупности )

 - выборочная средняя (среднее значение признака в выборочной совокупности)

P – генеральная доля (доля единиц, обладающих данным признаком в генеральной совокупности)

W – выборочная доля (доля, единиц обладающих данным признаком в выборочной совокупности)

 - генеральная дисперсия (дисперсия признака в генеральной совокупности)

 - выборочная дисперсия (дисперсия признака в выборочной совокупности)

t – коэффициент доверия при заданном уровне вероятности P

  В прикладных исследованиях часто возникает необходимость выяснить, различаются ли генеральные совокупности, из которых взяты две независимые выборки. Например, надо выяснить, влияет ли способ упаковки подшипников на их потребительские качества через год после хранения. Или: отличается ли потребительское поведение мужчин и женщин. Если отличается – рекламные ролики и плакаты надо делать отдельно для мужчин и отдельно для женщин. Если нет – рекламная кампания может быть единой.

         В математико-статистических терминах постановка задачи такова: имеются две выборки x₁, x₂,...,x_m и y₁, y₂,...,y_n (т. е. наборы из m и п действительных чисел), требуется проверить их однородность. Термин «однородность» уточняется ниже.

         Противоположным понятием является «различие». Можно переформулировать задачу: требуется проверить, есть ли различие между выборками. Если различия нет, то для дальнейшего изучения две рассматриваемые выборки часто объединяют в одну.

         Например, в маркетинге важно выделить сегменты потребительского рынка. Если установлена однородность двух выборок, то возможно объединение сегментов, из которых они взяты, в один. В дальнейшем это позволит осуществлять по отношению к ним одинаковую маркетинговую политику (проводить одни и те же рекламные мероприятия и т.п.). Если же установлено различие, то поведение потребителей в двух сегментах различно, объединять эти сегменты нельзя, и могут понадобиться различные маркетинговые стратегии, своя для каждого из этих сегментов.

         Традиционный метод проверки однородности (критерий Стьюдента). Для дальнейшего критического разбора опишем традиционный статистический метод проверки однородности. Вычисляют выборочные средние арифметические в каждой выборке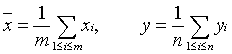

 ,

затем выборочные дисперсии

 ,  

и статистику Стьюдента t, на основе которой принимают решение,

  .    (1)

По заданному уровню значимости a и числу степеней свободы (m+n ^_ 2) из таблиц распределения Стьюдента находят критическое значение t_кр. Если |t|>t_кр, то гипотезу однородности (отсутствия различия) отклоняют, если же |t|<t_кр, то принимают. (При односторонних альтернативных гипотезах вместо условия |t|>t_кр проверяют, что t>t_кр; эту постановку рассматривать не будем, так как в ней нет принципиальных отличий от обсуждаемой здесь.)

         Рассмотрим условия применимости традиционного метода проверки однородности, основанного на использовании статистики t Стьюдента, а также укажем более современные методы.

         Вероятностная модель порождения данных. Для обоснованного применения эконометрических методов необходимо прежде всего построить и обосновать вероятностную модель порождения данных. При проверке однородности двух выборок общепринята модель, в которой x₁, x₂,...,x_m рассматриваются как результаты m независимых наблюдений некоторой случайной величины Х с функцией распределения F(x), неизвестной статистику, а y₁, y₂,...,y_n - как результаты п независимых наблюдений, вообще говоря, другой случайной величины Y с функцией распределения G(x), также неизвестной статистику. Предполагается также, что наблюдения в одной выборке не зависят от наблюдений в другой, поэтому выборки и называют независимыми.

          Возможность применения модели в конкретной реальной ситуации требует обоснования. Независимость и одинаковая распределенность результатов наблюдений, входящих в выборку, могут быть установлены или исходя из методики проведения конкретных наблюдений,или путем проверки статистических гипотез независимости и одинаковой распределенности с помощью соответствующих критериев [1].

          Если проведено (т+п) измерений объемов продаж в (т+п) торговых точках, то описанную выше модель, как правило, можно применять. Если же, например, x_i и y_i- объемы продаж одного и того же товара до и после определенного рекламного воздействия, то рассматриваемую модель применять нельзя. В последнем случае используют модель связанных выборок. В ней обычно строят новую выборку z_i = x_i - y_iи используют статистические методы анализа одной выборки, а не двух. Методы проверка однородности для связанных выборок рассматривается в разделе 3.1.6.

          При дальнейшем изложении принимаем описанную выше вероятностную модель двух выборок.

          Уточнения понятия однородности. Понятие «однородность», т. е. «отсутствие различия», может быть формализовано в терминах вероятностной модели различными способами.

          Наивысшая степень однородности достигается, если обе выборки взяты из одной и той же генеральной совокупности, т. е. справедлива нулевая гипотеза

H_{0 :} F(x)=G(x) при всех х.

Отсутствие однородности означает, что верна альтернативная гипотеза, согласно которой

H_{1 :} F(x₀)¹G(x₀)

хотя бы при одном значении аргумента x₀. Если гипотеза H₀  принята, то выборки можно объединить в одну, если нет - то нельзя.

          В некоторых случаях целесообразно проверять не совпадение функций распределения, а совпадение некоторых характеристик случайных величин Х и Y - математических ожиданий, медиан, дисперсий, коэффициентов вариации и др. Например, однородность математических ожиданий означает, что справедлива гипотеза

H'_{0 :} M(X)=M(Y),

где M(Х) и M(Y) - математические ожидания случайных величин Х и Y, результаты наблюдений над которыми составляют первую и вторую выборки соответственно. Доказательство различия между выборками в рассматриваемом случае - это доказательство справедливости альтернативной гипотезы 

H'_{1 :} M(X) ¹ M(Y .

          Если гипотеза H₀  верна, то и гипотеза H'₀ верна, но из справедливости H'₀ , вообще говоря, не следует справедливость H₀. Математические ожидания могут совпадать для различающихся между собой функций распределения. В частности, если в результате обработки выборочных данных принята гипотеза H'₀, то отсюда не следует, что две выборки можно объединить в одну. Однако в ряде ситуаций целесообразна проверка именно гипотезы H'_{0 .}  Например, пусть функция спроса на определенный товар или услугу оценивается путем опроса потребителей (первая выборка) или с помощью данных о продажах (вторая выборка). Тогда маркетологу важно проверить гипотезу об отсутствии систематических расхождений результатов этих двух методов, т.е. гипотезу о равенстве математических ожиданий. Другой пример – из производственного менеджмента. Пусть изучается эффективность управления бригадами рабочих на предприятии с помощью двух организационных схем, результаты наблюдения - объем производства на одного члена бригады, а показатель эффективности организационной схемы - средний (по предприятию) объем производства на одного рабочего. Тогда для сравнения эффективности препаратов достаточно проверить гипотезу H'₀ .

          Классические условия применимости критерия Стьюдента. Согласно математико-статистической теории должны быть выполнены два классических условия применимости критерия Стьюдента, основанного на использовании статистики t, заданной формулой (1):

         а) результаты наблюдений имеют нормальные распределения:

F(x)=N(x; m₁, s₁²), G(x)=N(x; m₂, s₂²)

с математическими ожиданиями m₁ и m₂ и дисперсиями s₁² и s₂² в первой и во второй выборках соответственно;

         б) дисперсии результатов наблюдений в первой и второй выборках совпадают:

D(X)=s₁²=D(Y)=s₂².

          Если условия а) и б) выполнены, то нормальные распределения F(x) и G(x) отличаются только математическими ожиданиями, а поэтому обе гипотезы H₀  и H'₀  сводятся к гипотезе

H"₀ : m₁=m₂, ,

а обе альтернативные гипотезы H₁ и H'₁ сводятся к гипотезе

H"₁ : m₁¹m₂, .

          Если условия а) и б) выполнены, то статистика t при справедливости H"₀имеет распределение Стьюдента с (т + п - 2) степенями свободы. Только в этом случае описанный выше традиционный метод обоснован безупречно. Если хотя бы одно из условий а) и б) не выполнено, то нет никаких оснований считать, что статистика t имеет распределение Стьюдента, поэтому применение традиционного метода, строго говоря, не обосновано. Обсудим возможность проверки этих условий и последствия их нарушений.

          Имеют ли результаты наблюдений нормальное распределение? Как показано в главе 2.1,априори нет оснований предполагать нормальность распределения результатов экономических, технико-экономических, технических, медицинских и иных наблюдений. Следовательно, нормальность надо проверять. Разработано много статистических критериев для проверки нормальности распределения результатов наблюдений [1]. Однако проверка нормальности - более сложная и трудоемкая статистическая процедура, чем проверка однородности (как с помощью статистики t Стьюдента, так и с использованием непараметрических критериев, рассматриваемых ниже).

          Для достаточно надежного установления нормальности требуется весьма большое число наблюдений. В главе 2.1 показано, что для того, чтобы гарантировать, что функция распределения результатов наблюдений отличается от некоторой нормальной не более чем на 0,01 (при любом значении аргумента), требуется порядка 2500 наблюдений. В большинстве технических, экономических, медицинских и иных исследований число наблюдений существенно меньше.

          Как уже отмечалось, есть и одна общая причина отклонений от нормальности: любой результат наблюдения записывается конечным (обычно 2-5) количеством цифр, а с математической точки зрения вероятность такого события равна 0. Следовательно, в прикладной статистике распределение результатов наблюдений практически всегда более или менее отличается от нормального распределения.  

          Последствия нарушения условия нормальности. Если условие а) не выполнено, то распределение статистики t не является распределением Стьюдента. Однако при справедливости H'₀  и условии б) распределение статистики t при росте объемов выборок приближается к стандартному нормальному распределениюФ(х)=N(x; 0, 1). К этому же распределению приближается распределение Стьюдента при возрастании числа степеней свободы. Другими словами, несмотря на нарушение условия нормальности традиционный метод (критерий Стьюдента) можно использовать для проверки гипотезы H'₀ при больших объемах выборок. При этом вместо таблиц распределения Стьюдента достаточно пользоваться таблицами стандартного нормального распределения Ф(х).

          Сформулированное в предыдущем абзаце утверждение справедливо для любых функций распределения F(x) и G(x) таких, что M(X)=M(Y), D(X)=D(Y) и выполнены некоторые внутриматематические условия, обычно считающиеся справедливыми в реальных задачах. Если же M(X)¹M(Y), то нетрудно вычислить, что при больших объемах выборок

P(t<x)»Ф(x-a_mn),             (2)

где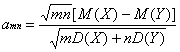

.               (3)

Формулы (2) - (3) позволяют приближенно вычислять мощность t-критерия (точность возрастает при увеличении объемов выборок т и п).