диплом саши. Реферат Ключевые слова биометрия, аутентификация, отпечаток пальца, преобразование Габора

• Название: Реферат Ключевые слова биометрия, аутентификация, отпечаток пальца, преобразование Габора
• Анкор: диплом саши.doc
• Дата: 19.12.2017
• Размер: 3.72 Mb.
• Имя файла: диплом саши.doc
• Тип: Реферат; #12167
• страница: 2 из 6

2.2 Исследование алгоритмов обработки образов отпечатков пальца

2.2.1 Алгоритмы обработки образов, основанные на сглаживающих или медианных фильтрах

Одни из наиболее часто используемых фильтров, используемых для обработки образов отпечатка пальца. Широкое распространение получили благодаря простоте реализации и низких требований к ресурсам вычислительной системы. Однако данные фильтры обеспечивают крайне невысокую степень фильтрации, к тому же побочным результатом их использования является размытие изображения, что отрицательно влияет на последующие шаги алгоритма распознавания образа.

2.2.2 Метод пространственной фильтрации образа, заключающейся в реализации физического процесса поглощения и отражения света

Плюсами данного метода является простота его реализации и достаточно высокое быстродействие; несмотря на простоту, конечное изображение не имеет характерной расфокусировки, свойственной широко распространенным сглаживающим и медианным алгоритмам. Так же данный алгоритм обеспечивает выделение середин папиллярных линий, что упрощает дальнейшую обработку отпечатка и выделение его скелета, что упрощает последующие шаги алгоритма распознавания образа отпечатка пальца. Минусами данного метода является худшее, по сравнению с более сложными фильтрами, качество фильтрации и сохранения ключевой информации.

2.2.3 Алгоритм обработки образов основанный на фильтрах Габора

Преимуществом данного метода является самое высокое качество обработки образов ОП из применяемых на сегодняшний день фильтров. Недостатком – самые высокие требования к вычислительной мощности из всех представленных алгоритмов.

Так как перед нами стоит задача выбрать алгоритм из условия качества фильтрации и сохранения ключевой информации, то наиболее рациональным выбором является алгоритм, основанный на фильтрах Габора, так как он лучше других удовлетворяет данным критериям.
2.3 Преобразование Габора

Рассмотри фильтр Габора в контексте нашей задач, а именно двумерный фильтр Габора.

2.3.1 Пространственный фильтра Габора для 2-D изображений

Формула функции Габора выглядит следующим образом:

,

где - комплексная синусоида, а - огибающая Гаусса для двумерного пространства. Остановимся более подробно на этих составных частях фильтра Габора.

2.3.2 Комплексная синусоида

Комплексная синусоида определяется как

,

где и Р определяются как пространственная частота и фаза синусоиды.

Можно представить синусоиду как две действительные функции, расположенные в действительной и мнимой части комплексной функции (Рисунок 2.1).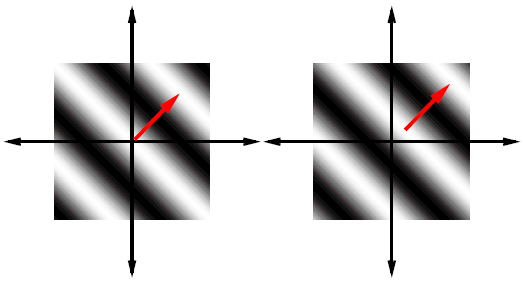



Рис. 2.1. Действительная и мнимая часть комплексной синусоиды с параметрами: , .

Действительная и мнимая части синусоиды имеют вид: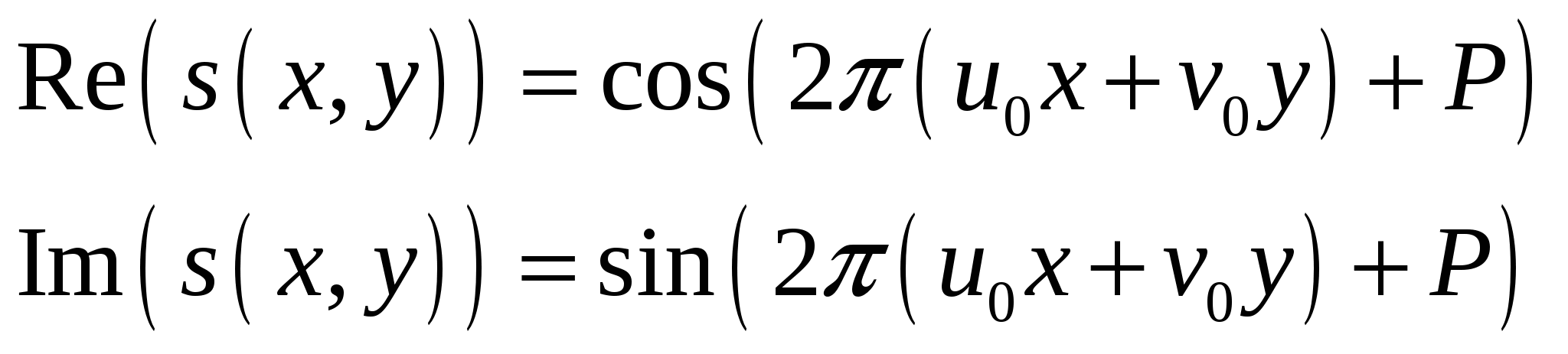



Параметры определяют частоту синусоиды в декартовых координатах.

2.3.3 Огибающая Гаусса

Огибающая Гаусса имеет вид:

,

где 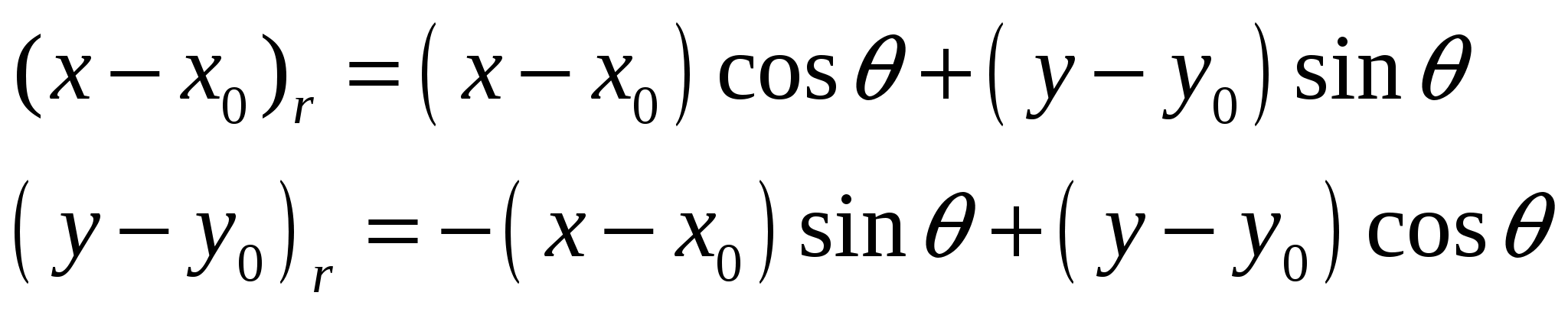- координаты пика функции, а и b скалярные параметры Гауссиана, - индекс, обозначающий операцию вращения, такой, что:

.

Иллюстрация огибающей Гаусса представлена на рисунке 2.2.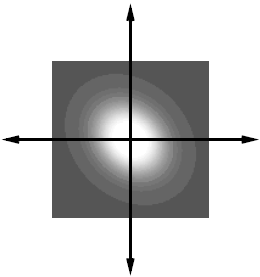



Рис.2.2. Огибающая Гаусса при значениях параметров:

2.3.4 Комплексная функция Габора

Комплексная функция Габора определяется следующими 9 параметрами:

• K Весовая величина огибающей Гаусса

• (a,b) Весовые величины огибающей, распределенные по осям

• Угол вращения огибающей Гаусса

• Координаты пика огибающей Гаусса

• Пространственные частоты комплексной синусоиды

• Р Фаза комплексной синусоиды

Каждая комплексная функция Габора состоит из двух частей, расположенных в действительной и мнимой части функции (Рисунок 2.3).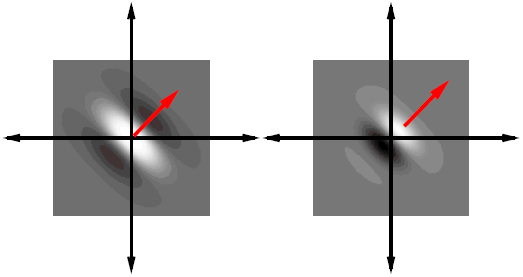



Рис.2.3 Действительная и мнимая часть комплексной функции Габора.

Таким образом, функция Габора имеет вид:



2.3.5 Алгоритм построения двумерного фильтра Габора

Для построения двумерного фильтра Габора применяется формула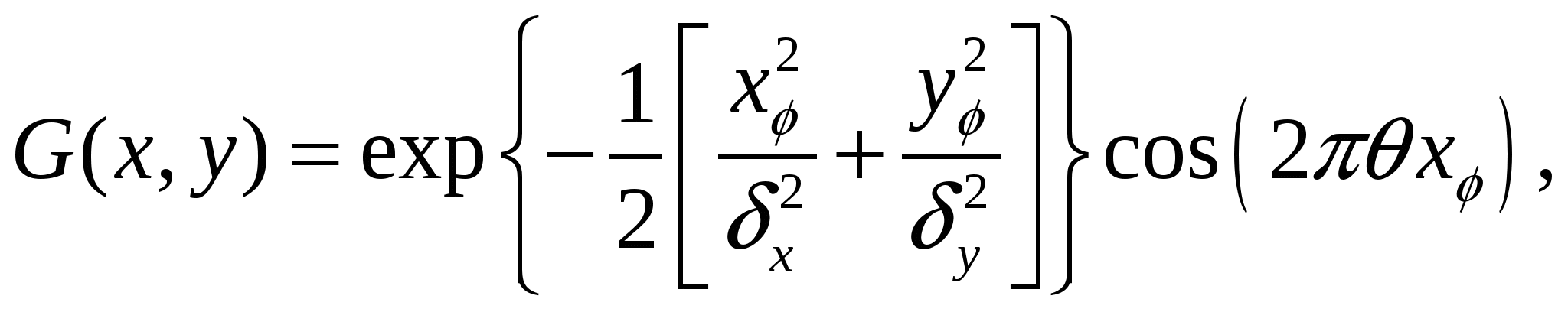



где , ; и - стандартные отклонения Гауссова ядра по осям соответственно, определяющая растянутость фильтра по осям; - частотная модуляция фильтра; - пространственное направление фильтра, определяющее ориентацию фильтра относительно осейx и y.

На Рисунке 2.4 изображена визуализация двумерной функции Габора в пространстве.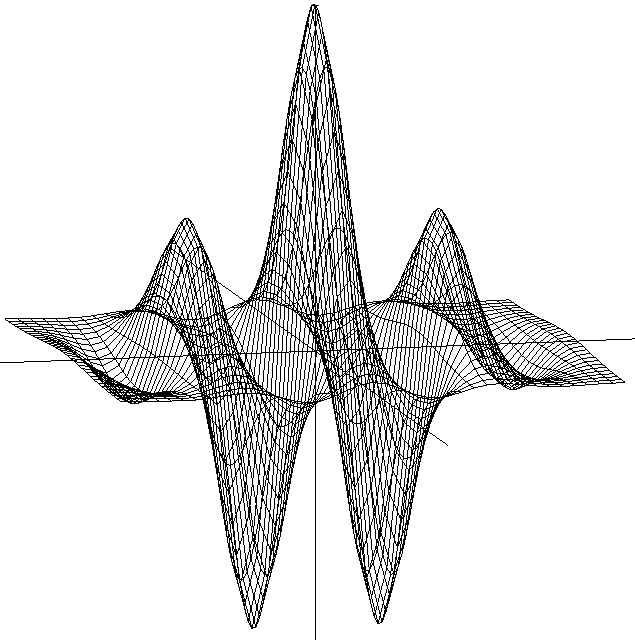



Рис.2.4. Двумерная функция Габора.
2.4 Применение фильтра Габора для 2-D изображений

Применение фильтра Габора для изображений осуществляется за четыре этапа.

Этап 1. Нормализация изображения.

Нормализация изображения необходима для того, чтобы задать предварительные средние значения и отклонения. Нормализованное изображение G определяется как 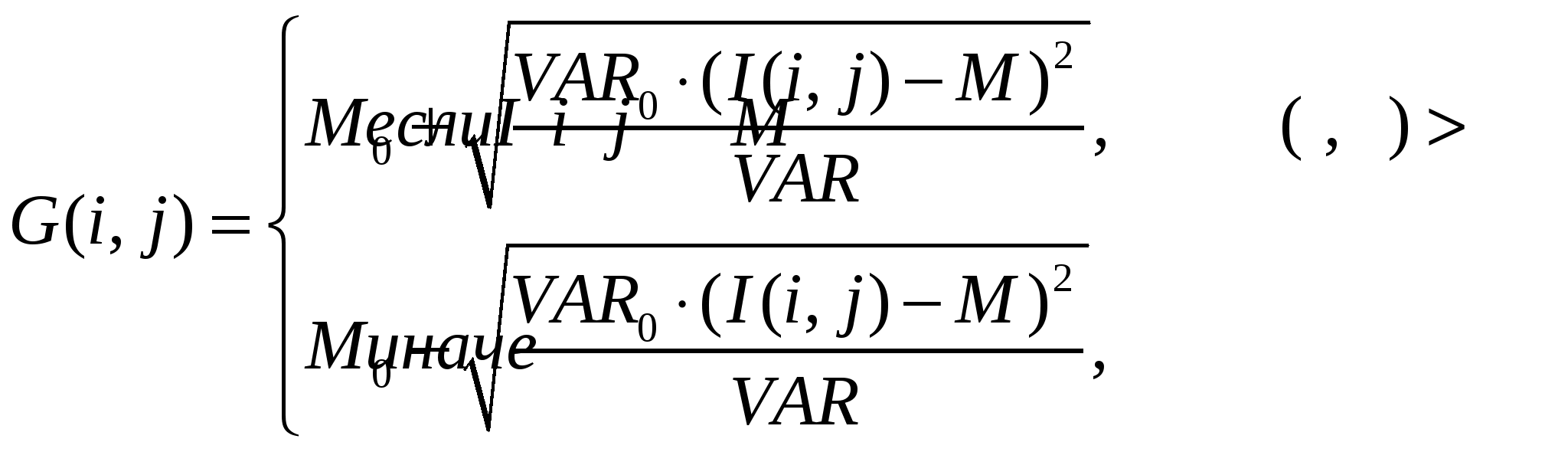изображение, где G(i,j) – значение нормализованной яркости пикселя с координатами (i, j). Нормализованное изображение рассчитывается исходя из среднего и среднеквадратического отклонения исходного изображения:

,

где и - заданные значения среднего и среднеквадратичного отклонения соответственно, и - исходные значения среднего и среднеквадратичного отклонения, вычисляются по формулам:

,



На рисунке 2.5 приведен пример входного и нормализованного изображения



(а) (б)

Рис.2.5. Пример входного (а) и нормализованного (б) изображения образа отпечатка пальца.

Этап 2. Расчет ориентационного изображения.

Рассчитываем рассчитывается ориентационное изображение. Ориентационное изображение О представляет собой матрицу 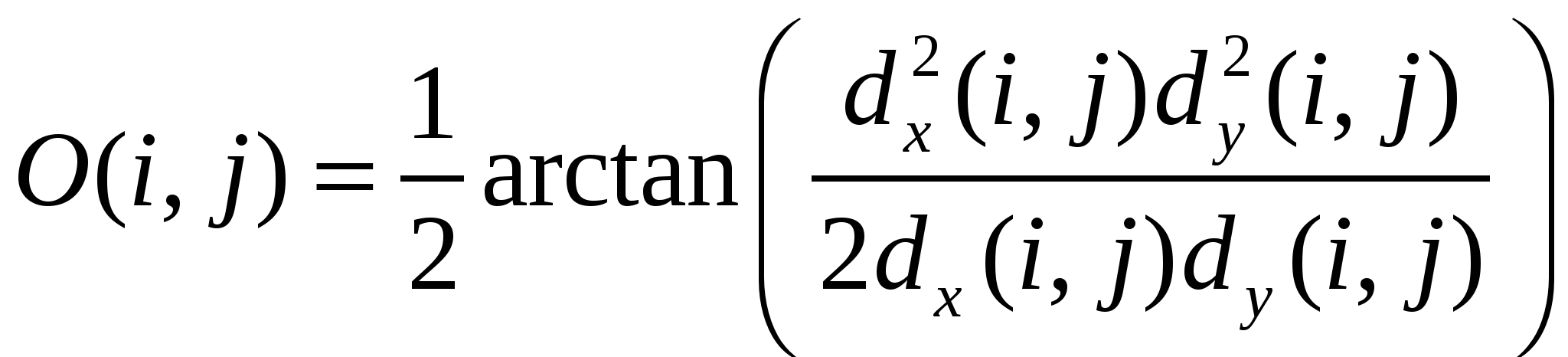, в которой каждая компонента показывает локальную ориентацию (угол наклона в данной точке) линии с координатами .

.

Пример ориентационного изображения отпечатка пальца показан на Рисунке 2.6.



а) б)

Рис.2.6. Ориентационные изображения фрагментов отпечатка пальца. На рисунке а) изображен фрагмент центра, на рисунке б) фрагмент дельты.

Этап 3. Расчет частотного изображения.

Частотное изображение представляет собой матрицу размера , в которой каждая компонента показывает локальную частоту линий в данной точке, определяемую как частоту гребней , направленных вдоль ориентации выступа. В случае, если в какой-то точке невозможно определить четкую синусоидально-очерченную волну (например, из-за наличие особых точек в этих координатах), частота определяется как средняя величина частоты в соседних блоках.



Рис.2.7. Пример блоков, в которых невозможно четко определить четкую синусоидально-очерченую волну.



Рис.2.8. Волновое представление линий в ячейке

Расчет частоты в точке с координатой рассчитывается следующим образом: если – количество пикселей между двумя соседними гребнями в блоке размерностью , и центр блока – пиксель с координатами , то частота в данной точке будет рассчитываться как



Этап 4. Бинаризация изображения.

Изображение B определяется как изображение, если каждый пиксель принимает одно из двух возможных значений – нуля единицы. Единица соответствует гребню отпечатка, ноль – впадине: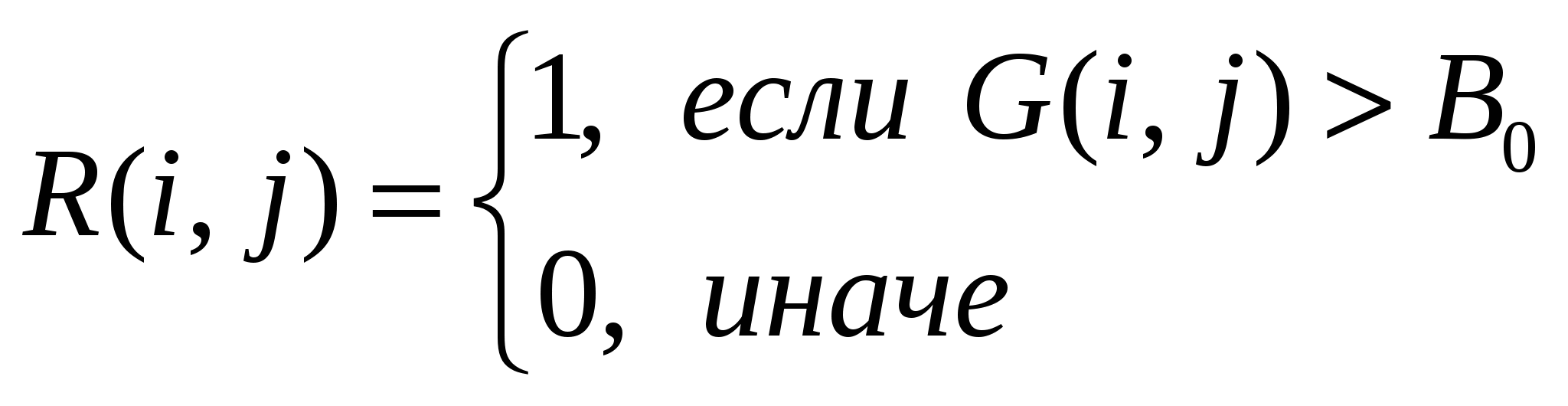

,

где - порог маскирования, а - интенсивность пикселя изображения.

Этап 5. Применение к бинарному изображению фильтров Габора.

Фильтр настраивается на локальную ориентацию выступов, применяется к пикселям выступов и впадин изображения.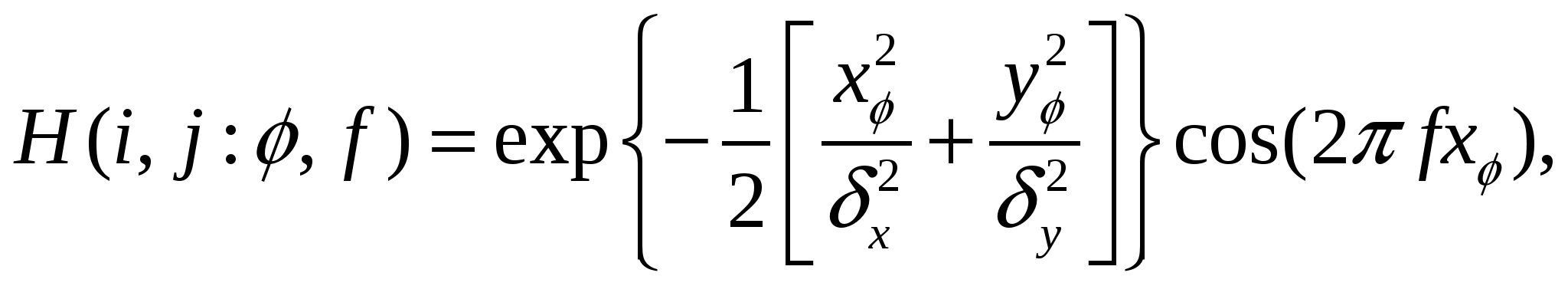



где ; ; - ориентация фильтра Габора, - частота, а и - пространственные константы огибающей Гаусса вдоль осей x и y соответственно.

Для использования Фильтра Габора нам необходимо знать значения следующих величин:

1) направление фильтра

2) частоту синусоидальной плоскостной волны

3) и - среднеквадратичные отклонения огибающей Габора

Частотная характеристика фильтра определяется из локальной частоты f выступов, направление определяется локальной ориентацией. Значения и можно задать при реализации алгоритма. Чем больше будут эти значения, тем более фильтр будет устойчив к шумам, но, в то же время, будет вносить больше искажений, создавая несуществующие выступы и впадины. Если выбрать значения и низкими, фильтр не будет вносить искажений, но его способность фильтровать значительно снизится, что приведет к неэффективному устранению шумов. Поэтому при подборе значений и пытаются найти компромисс между эффективностью фильтра и отсутствием вносимых фильтром искажений. Как правило эти параметры подбираются эмпирическим путем.



Рис.2.9. Пример отпечатка пальца, обработанного фильтром Габора.

2.5 ROC-анализ

Пусть имеется два класса: с положительным исходом и с отрицательным исходом. ROC-кривая показывает зависимость количества верно классифицированных положительных примеров от количества неверно классифицированных отрицательных примеров. В терминологии ROC-анализа первые называются истинно положительным, вторые – ложно отрицательным множеством. При этом предполагается, что у классификатора имеется некоторый параметр, варьируя который, мы будем получать то или иное разбиение на два класса. Этот параметр часто называют порогом, или точкой отсечения (cut-off value). В зависимости от него будут получаться различные величины ошибок I и II рода. Для понимания сути ошибок I и II рода рассмотрим Таблицу 2.1.

Таблица 2.1 Ошибки первого и второго рода

	Фактически
Моедель	Положительно	Отрицательно
Положительно	TP	FP
Отрицательно	FN	TN

TP (True Positives) – верно классифицированные положительные примеры (так называемые истинно положительные случаи);

TN (True Negatives) – верно классифицированные отрицательные примеры (истинно отрицательные случаи);

FN (False Negatives) – положительные примеры, классифицированные как отрицательные (ошибка I рода). Это так называемый "ложный пропуск" – когда интересующее нас событие ошибочно не обнаруживается (ложно отрицательные примеры);

FP (False Positives) – отрицательные примеры, классифицированные как положительные (ошибка II рода); Это ложное обнаружение, т.к. при отсутствии события ошибочно выносится решение о его присутствии (ложно положительные случаи).

Для нашей задачи положительным исходом будет класс гребней (черные пиксели в для изображения), отрицательным исходом – класс впадин (белые пиксели).

При анализе чаще оперируют не абсолютными показателями, а относительными – долями, выраженными в процентах:

Доля истинно положительных примеров:

.

Доля ложно положительных примеров:

.

Введем еще два определения: чувствительность и специфичность модели. Ими определяется объективная ценность любого бинарного классификатора.

Чувствительность – это и есть доля истинно положительных случаев:

,

Специфичность – доля истинно отрицательных случаев, которые были правильно идентифицированы моделью:

,

Заметим, что .

Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры). Если рассуждать в терминах нашей задачи:

• 
  Чувствительный тест характеризуется максимальном предотвращении пропуска гребня;
  
• 
  Специфичный тест диагностирует только истинные гребни. Это важно в случае, когда «гипердиагностика» не желательна.
  

ROC-кривая получается следующим образом:

1. Для каждого значения порога отсечения, которое меняется от 0 до 1 с шагом dx (например, 0.01) рассчитываются значения чувствительности Se и специфичности Sp. В качестве альтернативы порогом может являться каждое последующее значение примера в выборке.

2. Строится график зависимости: по оси у откладывается чувствительность Se, по оси х откладываем величину 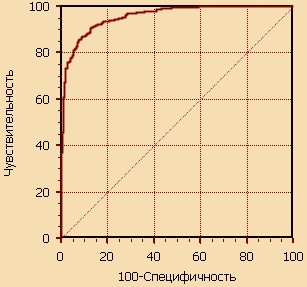(сто процентов минус специфичность), или, что то же самое, FPR – доля ложно положительных случаев.



Рис 2.10. ROC-кривая

Для идеального классификатора график ROC-кривой проходит через верхний левый угол, где доля истинно положительных случаев составляет 100% или 1.0 (идеальная чувствительность), а доля ложно положительных примеров равна нулю. Поэтому чем ближе кривая к верхнему левому углу, тем выше предсказательная способность модели. Наоборот, чем меньше изгиб кривой и чем ближе она расположена к диагональной прямой, тем менее эффективна модель. Диагональная линия соответствует "бесполезному" классификатору, т.е. полной неразличимости двух классов.
2.6 Подбор параметров алгоритма. Математическая постановка задачи