Теория удара. Реферат Тема Теория удара План реферата Введение
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
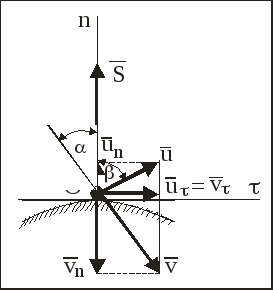
Косой удар материальной точки о неподвижную поверхностьКосым ударом МТ с массой m об абсолютно гладкую неподвижную поверхность, называется такой удар, при котором скорость Пусть угол – угол падения, а скорость в конце удара направлена к этой нормали под некоторым углом – угол отражения (рис. 2).
Из последнего равенства следует, что то есть касательная составляющая скорости МТ при ударе об идеальную гладкую поверхность не изменяется. Так как влиянием трения пренебрегаем и, следовательно, удар происходит только по направлению нормали к поверхности в точке удара, то аналогично соотношению (4), запишем: В результате из соотношений (5) и (6) можно найти модуль и направление скорости МТ в конце удара и ударный импульс, если m, v и k известны [6]: На рис. 2 видно, что Поделив эти соотношения почленно и учтя, что то есть в случае косого удара коэффициент восстановления есть отношение тангенса угла падения к тангенсу угла отражения. При не вполне упругом ударе В частном случае абсолютно упругого удара Теорема об изменении количества движения системы материальных точек при ударе Рассмотрим систему материальных точек (далее – СМТ), состоящую из n МТ, и выделим -ю МТ с массой Так же как при доказательстве общих теорем динамики СМТ, разделим все ударные импульсы, действующие на МТ, на внешние и внутренние. Тогда основное уравнение теории удара (1) для -й МТ рассматриваемой СМТ примет вид [6]: где Составив такие уравнения для всех n МТ рассматриваемой СМТ и сложив их почленно, получим [2, 3, 6]: Введя следующие обозначения: Теорема: Изменение количества движения СМТ за время удара равно геометрической сумме всех внешних ударных импульсов, действующих на эту СМТ. Проектируя соотношение (8) на координатные оси, получим скалярную форму теоремы об изменении количества движения СМТ при ударе [6]: 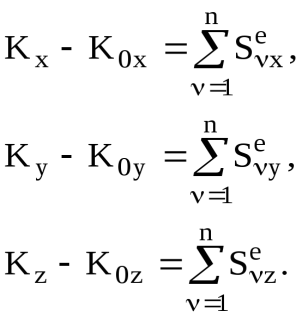 (9) (9)Из соотношений (9) следует, что изменение проекции количества движения СМТ на какую-либо ось за время удара равно сумме проекций всех ударных импульсов внешних ударных сил, действующих на СМТ, на ту же ось. |

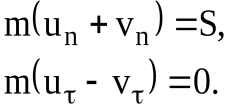 (5)
(5)