Теория удара. Реферат Тема Теория удара План реферата Введение

• Название: Реферат Тема Теория удара План реферата Введение
• Анкор: Теория удара
• Дата: 01.02.2023
• Размер: 0.88 Mb.
• Имя файла: Doklad_po_teme_Alexeev_IA.docx
• Тип: Реферат; #915555
• страница: 3 из 9

3.1.2. Абсолютно неупругий удар

Абсолютно неупругий удар — ударное взаимодействие, в результате которого тела соединяются и продолжают дальнейшее своё движение как единое тело. Его скорость может быть найдена из закона сохранения импульса. Важно отметить, что импульсы являются величинами векторными, поэтому складываются только векторно [6]:

,

где v → {\displaystyle {\vec {v}}} это общая скорость тел, полученная после удара, m a {\displaystyle m_{a}} и v → a {\displaystyle {\vec {v}}_{a}}  — масса и скорость первого тела до соударения, m b {\displaystyle m_{b}} и v → b {\displaystyle {\vec {v}}_{b}}  — масса и скорость второго тела до соударения. Важно отметить, что импульсы являются величинами векторными, поэтому складываются только векторно [6]:

.

Как и при любом ударе, при этом выполняются закон сохранения импульса и закон сохранения момента импульса, но не выполняется закон сохранения механической энергии. Часть кинетической энергии соударяемых тел в результате неупругих деформаций переходит в тепловую. В случае абсолютно неупругого удара механическая энергия уменьшается на максимально возможную величину, не противоречащую закону сохранения импульса. Данное утверждение можно принять за определение абсолютно неупругого удара в терминах энергии. При помощи теоремы Кёнинга легко показать, что в этом случае тела продолжают движение как единое целое: компонента кинетической энергии, отвечающая за движение центра масс всей системы соударяемых тел, должна остаться неизменной в силу закона сохранения импульса, а кинетическая энергия в системе отсчёта, связанной с центром масс, будет минимальной в том случае, когда тела в ней покоятся.

Наиболее простая модель абсолютно неупругого удара — сталкивающиеся пластилиновые шарики.

3.1.3. Реальный удар

При реальном соударении тел наблюдаются промежуточные варианты между случаем абсолютно упругого удара — отскока, и случаем абсолютно неупругого удара — слипания соударяющихся тел.

Степень близости соударения в случаю абсолютно упругого удара характеризуют коэффициентом восстановления k {\displaystyle k} . При k = 0 {\displaystyle k=0} удар является абсолютно неупругим, при k = 1 {\displaystyle k=1} удар является абсолютно упругим.

Пусть u 1 , u 2 {\displaystyle u_{1},u_{2}}  — скорости тел до удара, v 1 , v 2 {\displaystyle v_{1},v_{2}}  — скорости тел после удара, k {\displaystyle k} -коэффициент восстановления, S {\displaystyle S}  — полный импульс удара. Тогда [3, 6]:

v 1 = u 1 − ( 1 + k ) m 2 m 1 + m 2 ( u 1 − u 2 ) {\displaystyle v_{1}=u_{1}-(1+k){\frac {m_{2}}{m_{1}+m_{2}}}(u_{1}-u_{2})} ,

v 2 = u 2 + ( 1 + k ) m 1 m 1 + m 2 ( u 1 − u 2 ) {\displaystyle v_{2}=u_{2}+(1+k){\frac {m_{1}}{m_{1}+m_{2}}}(u_{1}-u_{2})} ,

S = ( 1 + k ) m 1 m 2 m 1 + m 2 ( u 1 − u 2 ) {\displaystyle S=(1+k){\frac {m_{1}m_{2}}{m_{1}+m_{2}}}(u_{1}-u_{2})} .

Потеря кинетической энергии T {\displaystyle T} при ударе [6]:

T = ( 1 − k 2 ) m 1 m 2 m 1 + m 2 ( u 1 − u 2 ) 2 2 = 1 − k 1 + k [ m 1 ( u 1 − v 1 ) 2 2 + m 2 ( u 2 − v 2 ) 2 2 ] {\displaystyle T=(1-k^{2}){\frac {m_{1}m_{2}}{m_{1}+m_{2}}}{\frac {(u_{1}-u_{2})^{2}}{2}}={\frac {1-k}{1+k}}\left[{\frac {m_{1}(u_{1}-v_{1})^{2}}{2}}+{\frac {m_{2}(u_{2}-v_{2})^{2}}{2}}\right]} .

Для абсолютно неупругого удара k = 0 {\displaystyle k=0} : T = m 1 ( u 1 − v 1 ) 2 2 + m 2 ( u 2 − v 2 ) 2 2 {\displaystyle T={\frac {m_{1}(u_{1}-v_{1})^{2}}{2}}+{\frac {m_{2}(u_{2}-v_{2})^{2}}{2}}} , то есть потерянная кинетическая энергия равна кинетической энергии потерянных скоростей, что следует из теоремы Карно.

Для абсолютно упругого удара k = 1 {\displaystyle k=1} T = 0 {\displaystyle T=0} .

Кроме того, при реальном ударе макроскопических тел происходит деформация соударяющихся тел и распространение по ним упругих волн, передающих взаимодействие от сталкивающихся границ по всему телу.

Пусть сталкиваются одинаковые тела. Если c — скорость звука в теле, L — характерный размер каждого тела, то время удара будет порядка t = 2 L / c {\displaystyle t=2L/c}  — двукратному прохождению волны деформации вдоль линии соударения, что учтено множителем 2 соответствующем распространению волны в прямом и обратном направлении.

Систему сталкивающихся тел можно считать замкнутой, если импульс силы внешних сил за время соударения мал по сравнению с импульсами тел.

Кроме того, само время соударения должно быть достаточно мало, иначе при рассмотрении трудно оценить потери энергии на упругую деформацию за время удара, и при этом часть энергии расходуется на внутреннее трение, а само описание сталкивающихся тел становится сложным из-за существенного вклада внутренних колебательных степеней свободы.

В приведенном анализе необходимо, чтобы линейные деформации тел при ударе были существенно меньше, чем собственные размеры тел.

3.2. Анализ процессов удара материальных объектов
Для анализа ударного взаимодействия рассмотрим материальную точку (далее – МТ) с массой m, которая движется под действием обычной (неударной) силы . В момент , когда рассматриваемая МТ имеет скорость – скорость до удара, на нее начинает действовать ударная сила , действие которой прекращается в момент . Определим движение МТ под действием сил и за время удара .

Применяя теорему об изменении количества движения МТ, получим [6]: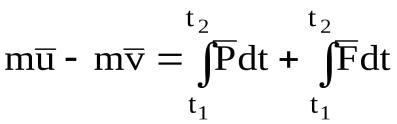

,

где – скорость точки в момент после удара.

Рассмотрим отдельно каждый член правой части этого равенства. По теореме о среднем значении определенного интеграла можно написать [6]: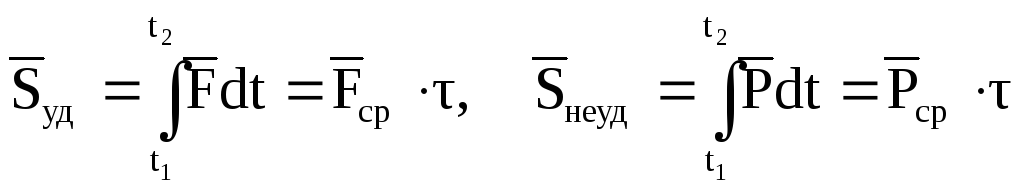

,

где и есть средние значения сил и в некоторый промежуток времени. При этом является конечной величиной; ударная сила за время удара достигает весьма большой величины (порядка ). Поэтому произведение будет пренебрежимо мало по сравнению с произведением , являющимся величиной конечной. Импульс обычной (неударной) силы за время удара будет по сравнению с импульсом ударной силы очень мал и им можно пренебречь.

В итоге [6]:

(1).
Основное уравнение теории удара

Изменение количества движения МТ за время удара равно действующему на эту МТ ударному импульсу.

Проектируя векторное равенство (1) на координатные оси, получим три следующих уравнения [1, 6]: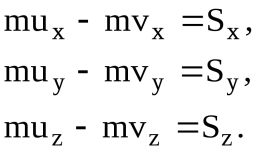

(2)

Таким образом, изменение проекции количества движения материальной точки на какую-нибудь неподвижную ось за время удара равно проекции на ту же ось действующего на эту точку ударного импульса.

Уравнение (1) – основное уравнение теории удара, которое играет такую же роль в явлении удара, как второй закон динамики при изучении движений под действием обычных сил.

Определим перемещение МТ за время удара.

Так как , где – радиус-вектор, определяющий положение данной МТ относительно некоторой системы отсчета, то уравнение (1) можно записать следующим образом [6]:



Проинтегрировав это равенство в пределах от до , получаем [6]:

,

где есть среднее значение ударного импульса за время удара . Учитывая при этом, что и суть величины конечные, а - весьма мало, приходим к выводу, что будет близко к нулю и, следовательно, за время удара перемещение МТ практически равно нулю.

Таким образом, перемещением МТ за время удара можно пренебречь, считая, что за время удара эта МТ практически остается неподвижной, то есть не успевает переместиться.