ШПОРА НА ЗАДАЧИ. Решение номинал дополнительно размещенных акций номиналу существующих, поэтому число дополнительных акций

• Название: Решение номинал дополнительно размещенных акций номиналу существующих, поэтому число дополнительных акций
• Анкор: ШПОРА НА ЗАДАЧИ.doc
• Дата: 15.02.2017
• Размер: 176.5 Kb.
• Имя файла: ШПОРА НА ЗАДАЧИ.doc
• Тип: Решение; #2732
• страница: 1 из 9

Задача1
Акционерное общество с уставным капиталом 2 млн. рублей, состоящем из 100000 обыкновенных акций, осуществляет дополнительный выпуск акций. Курсовая стоимость акций – 10 рублей. Номинал эмиссии дополнительных акций – 2 млн. рублей. Для организации выпуска привлечен андеррайтер, который берет на себя обязательство выкупить весь выпуск акций. Плата за андеррайтинг установлена как максимально возможная (в рамках закона). Рассчитайте размер вознаграждения андеррайтера
Решение

1. номинал дополнительно размещенных акций = номиналу существующих, поэтому число дополнительных акций:

2 000 000 (номинал новой эмиссии) / ((2 000 000 (УК) / 100 000 (количество существующих акций) – частное от деления равно номиналу 1 обыкновенной акции) = 100 000

Это в общем случае, но для целей этой задачи можно заметить, что номинал допэмиссии равен уставному капиталу, поэтому и акций размещается столько же, сколько уже размещено.

2. Сумма привлеченных средств = курсовая стоимость всех дополнительно размещенных акций = 10 * 100 000 = 1 000 000 руб.

3. Андеррайтер по законодательству может взимать плату за услуги в пределах 10% от цены размещения, то есть вознаграждение равно:

10% * 1 000 000 = 100 000 руб.

Ответ: 100 000 руб.
Задача 2
Акционерным обществом при учреждении размещено 50000 акций с номинальной стоимостью 100 рублей. В уставе зафиксировано 10000 объявленных акций номинальной стоимостью 1000 рублей. На вторичном рынке акции продаются по цене 1200 рублей. Рассчитайте величину уставного капитала общества и его рыночную стоимость
Решение:

В данном случае нам неинтересны объявленные акции, поскольку, сколько бы их ни было зафиксировано в уставе, пока они не размещены и не увеличивают уставного капитала. Тогда:

Величина УК = цена размещенных акций * их количество = 50 000 * 100 = 5 000 000 руб.

Рыночная стоимость УК = капитализация = цена акций на вторичном рынке * их число =

1 200 * 50 000 = 60 000 000 руб.

Ответ: 5 млн. руб., 60 млн. руб.
Задача 3
Инвестор купил облигацию по цене 1010 руб и продал ее через два года за 995 руб. За двухлетний период он получил купонные платежи в сумме 300 руб. Какую доходность за период и в расчете на год он получил. Годовую доходность определять на базе сложных процентов.
Решение:

Доходность за период = (Цена продажи + купонный доход – цена покупки) / цена покупки * 100% = (995 + 300 – 1010) / 1010 * 100% = 28,22%

Доходность за год на базе сложных %ов:



Ответ: 28,22%; 13,23%


Задача 4
Определить рыночную цену (в долларах) купонной облигации, выпущенной в 1980г., если в момент эмиссии фиксированная купонная ставка была установлена в размере 10%, проценты по облигации выплачиваются 1 раз в год, а в момент продажи доходность до погашения облигации с аналогичным рейтингом равнялась 8%. Номинал облигации равен 1000 долл. Облигация продается на следующий день после выплаты очередного купонного дохода и до погашения облигации остается два года. По условиям эмиссии облигация погашается с 10% премией.
Решение:

Цена облигации определяется по формуле:

V = INT * PVIFA + M * PVIF = M * q * PVIFA + M * PVIF, где

INT – купонный платеж,

q – ставка купона,

M – номинал облигации (или сумма, полученная при погашении).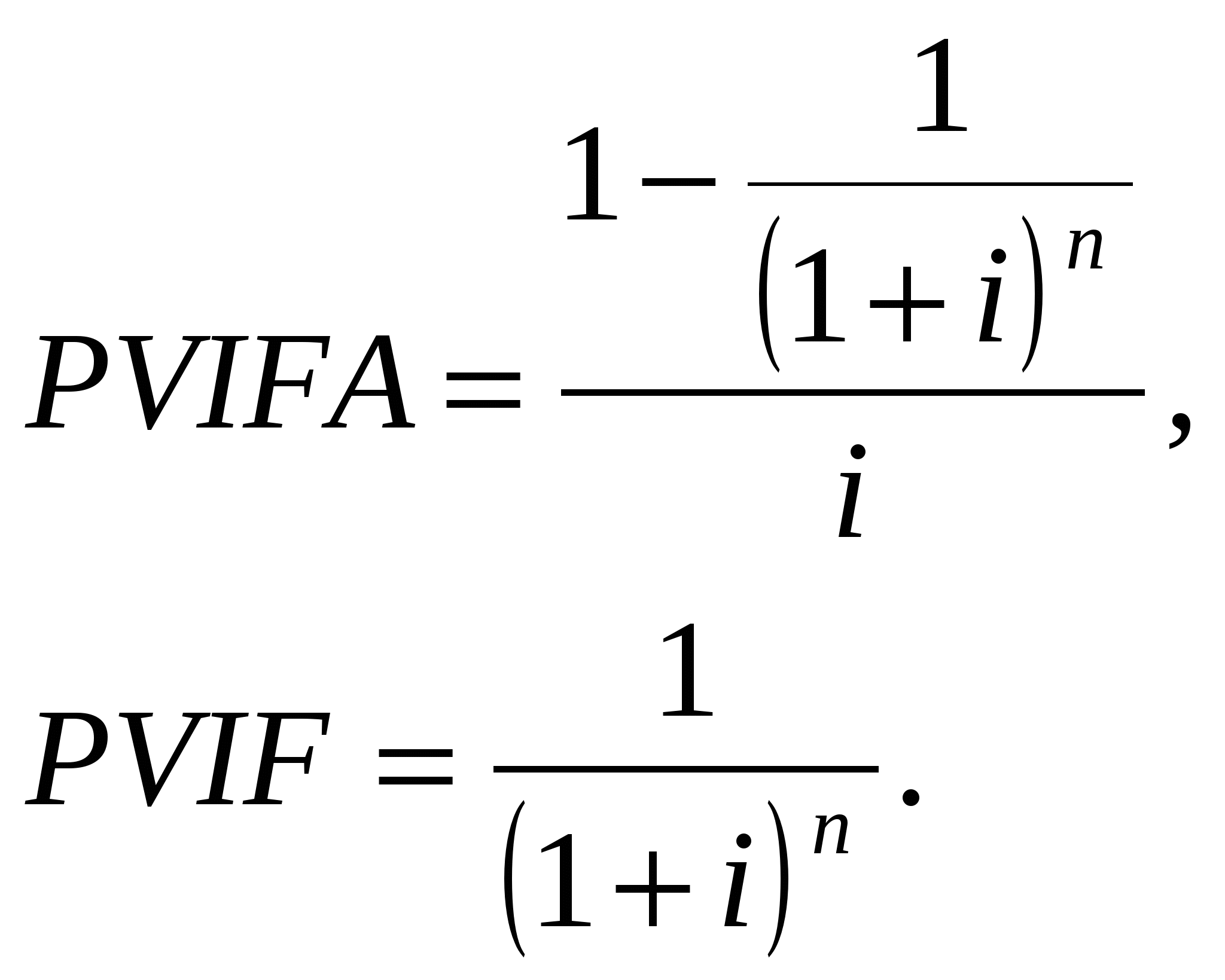



Тогда с учетом того, что n = 2, i = 8%, q = 10%, M = 1000 * 1,1= 1100,

V = 1121,4 долл.

Ответ: 1121,4 долл.

Задача 5

Чистая прибыль АО «Пионер» составила 1 000 000 рублей. Акции этого общества (их выпущено 4 000 штук) продаются на рынке по цене 2000 рублей за акцию. Рассчитайте показатель дохода на акцию (EPS) и коэффициент р/е.
Решение:

В данном случае EPS = ЧП / число ао в обращении = 1 000 000 / 4 000 = 250 руб.

P/E = цена / EPS = 2 000 / 250 = 8

Ответ: 250 руб; 8.

Задача 6

Рассчитайте, что выгоднее, купить 1000 облигаций номиналом 1000 рублей со сроком обращения 1 год и ставкой купона 20 % (выплачивается 2 раза в год) по цене 112%, или положить 1млн. руб. в банк на тот же срок с процентной ставкой по депозиту 19 % и начислением процентов раз в год? Предусматривается возможность реинвестирования процентов по облигации по банковской процентной ставке. Налогообложение не учитывается. Указать величину доходности более выгодного инструмента с точностью до сотых.
Решение:

Доход по облигациям складывается из 3 компонентов: разницы цены приобретения и номинала; купонного дохода; дохода от реинвестирования купонов (в нашем случае только первого купонного платежа и на полгода). Доходность по облигациям:

1000 * (1000 * (1 – 1,12) + 1000 * 0,2 + 1000 * 0,1 * 0,19 / 2) / (1000 * 1000 * 1,12) = 7,99%

Доходность по вкладу равна 19,00%.

В данном случае выгоднее положить деньги в банк.

Ответ: в банке выгоднее (19,00% против 7,99%).