Решение одноиндексных оптимизационных задач. ЛР № 2. Решение одноиндексных оптимизационных задач Цель работы научиться решать одноиндексные оптимизационные задачи производства
 Скачать 4.38 Mb. Скачать 4.38 Mb.
|
|
Задача проверки сбалансированности плана Рассмотрим решение предыдущей задачи при измененных условиях. Предположим при сложившейся ситуации на рынке продукцию вида D сняли с производства и взамен планируется выпуск продукции вида Е. Поменялись предельно допустимые значения выпуска некоторых видов. Все исходные данные по расходу, запасам ресурсов, предельно допустимым значениям выпуска каждого вида даны в табл. 2.7. Таблица 2.7. Условие задачи 2
Прибыль от реализации единицы продукции равны: 8 д. е. – для A, 10 д. е. – для B, 7 д. е. – для C, 12 д. е. – для Е. Необходимо определить объем продукции каждого вида, чтобы прибыль от реализации продукции была максимальной. Решение. Составим математическую модель для решения поставленной задачи. Обозначим переменные: x1 – объем произведенной продукции вида А; x2 – объем произведенной продукции вида B; x3 – объем произведенной продукции вида C; x4 – объем произведенной продукции вида Е. Прибыль от реализации продукции составит: Ограничения для переменных: 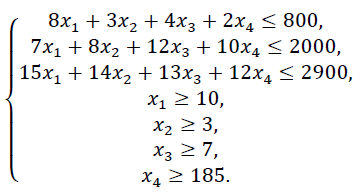 Математическая постановка данной задачи состоит в нахождении такого неотрицательного решения системы линейных уравнений, при котором целевая функция F принимает максимальное значение. Создадим на рабочем листе таблицу для ввода исходных данных. Введем в созданную таблицу исходные данные, целевую функцию, ограничения и граничные условия (рис. 2.31). 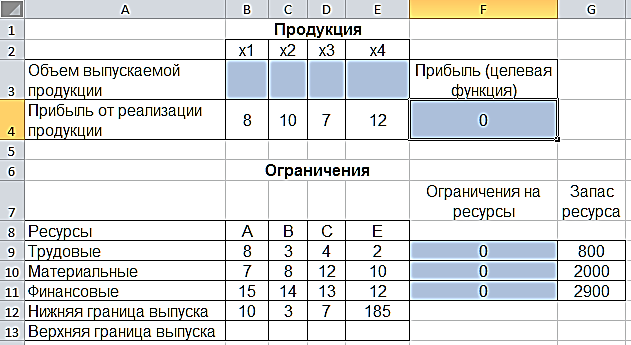 Рис. 2.31. Исходные данные для задачи 2 В формульном варианте таблица будет иметь вид (рис. 2.32): 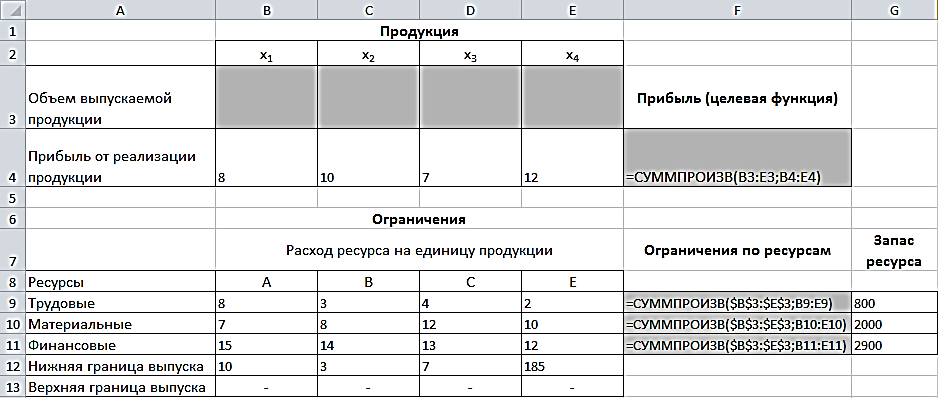 Рис. 2.32. Формулы для вычислений На вкладке «Данные» в группе «Анализ» выберем команду «Поиск решения». На экране отобразится диалоговое окно «Параметры поиска решения», в котором установим необходимые параметры (рис. 2.33): 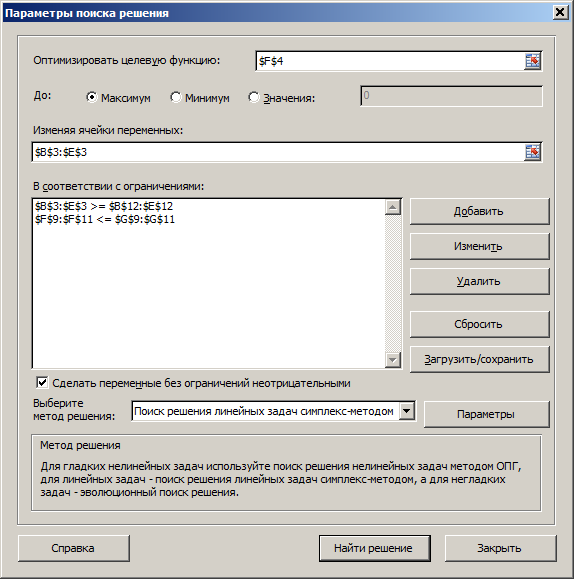 Рис. 2.33. Окно «Параметры поиска решения» задачи 2 После выбора кнопки Найти решение отобразится окно Результаты поиска решения (рис. 2.34).  Рис. 2.34. Окно «Результаты поиска решения» задачи 2 В данном окне дано сообщение, что в результате решения данной задачи не удалось найти допустимого решения. Выведем отчет о допустимости (рис 2.35). 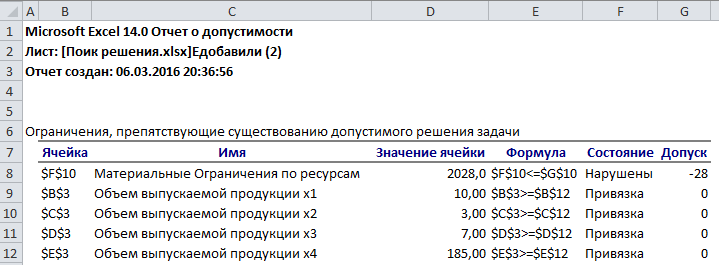 Рис. 2.35. Отчет о допустимости По отчету о допустимости делаем вывод, что задача не сбалансирована по материальным ресурсам. Действительно, если подставим нижние границы выпуска продукции во второе уравнение системы , то материальных ресурсов для выполнения плана не хватит: 7*10+8*3+12*7+10*185 = 2028 (запас материальных ресурсов по условию задачи равен 2000 ед.). Поэтому мы и не получили оптимального решения. При постановке задачи определения оптимального ассортимента продукции до получения ее решения неизвестно, сбалансирована она или нет. В этом случае есть смысл составить модель с учетом возможной нехватки ресурсов. Введем новые переменные: объем дополнительных трудовых ресурсов; объем дополнительных материальных ресурсов; объем дополнительных финансовых ресурсов. Дополнительные ресурсы необходимы для выполнения скорректированного плана производства. Теперь задача сводится к минимизации целевой функции L. Предприятие заинтересовано в получаемой прибыли. Поэтому включим ее желаемое значение в систему ограничений: 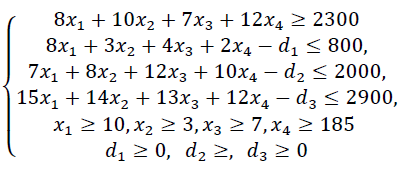 Математическая постановка скорректированной задачи состоит в нахождении такого неотрицательного решения системы линейных неравенств, при котором целевая функция L принимает минимальное значение. Создадим на рабочем листе таблицу для ввода исходных данных. Введем в созданную таблицу исходные данные, целевую функцию, ограничения и граничные условия (рис. 2.36). Диапазон ячеек В3:Е3;G9:G11 содержит оптимальное решение, значение этих ячеек будет получено в результате решения задачи. Блок ячеек В4:Е4 содержит значения прибыли от реализации продукции. В ячейках В9: Е13 отображен расход ресурсов на единицу производства продукции A, B, C и Е и предельно допустимые значения выпуска каждого вида. Для вычисления прибыли в ячейке F4 используем функцию =СУММПРОИЗВ($B$3:$E$3;B4:E4). В ячейки F9:F11 введены формулы для расчета ограничений по ресурсам. Целевая функция находится в ячейке G14. 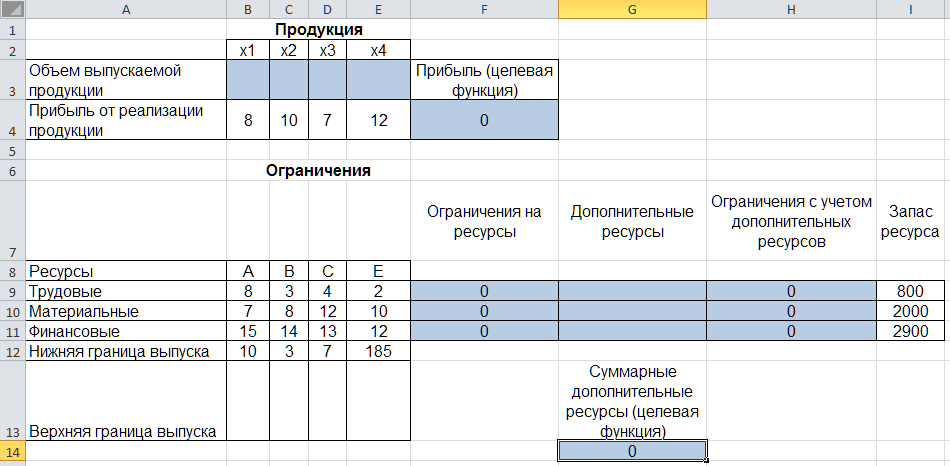 Рис. 2.36. Окно исходных данных задачи 2 В формульном варианте таблица будет иметь вид (рис. 2.37): 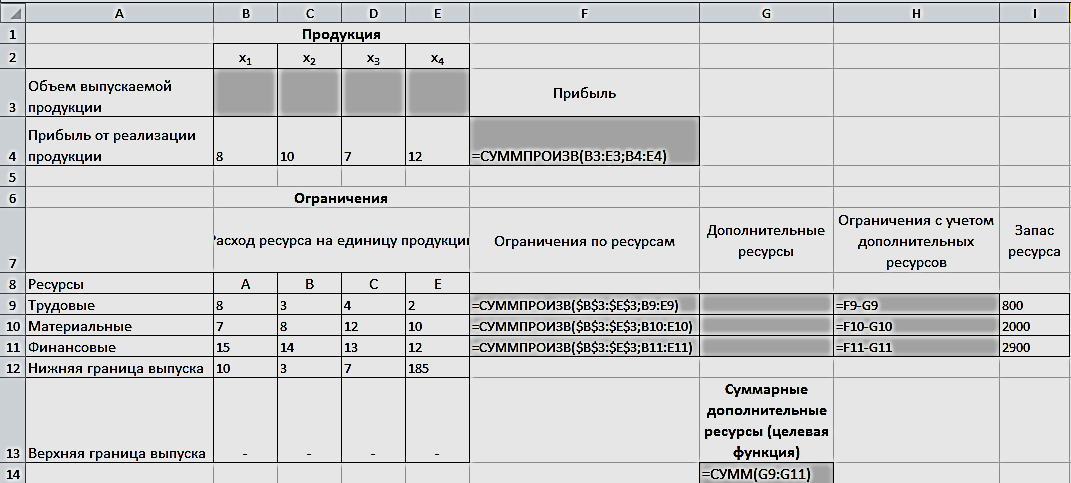 Рис. 2.37. Формулы для расчета задачи 2 На вкладке «Данные» в группе «Анализ» выберем команду «Поиск решения». На экране отобразится диалоговое окно Параметры поиска решения, в котором установим необходимые параметры (рис. 2.23) для решения задачи. 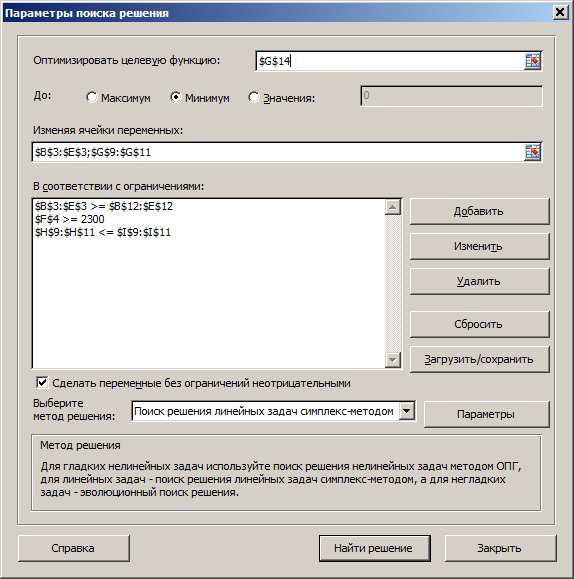 Рис. 2.38. Окно «Параметры поиска решения» После выбора кнопки Найти решение отобразится окно Результаты поиска решения (рис. 2.39). В данном окне дано сообщение, что решение найдено.  Рис. 2.39. Результаты поиска решения задачи 2 Для сохранения полученного решения необходимо установить переключатель «Сохранить найденное решение» и нажать кнопку ОК. После чего на рабочем листе отобразится решение задачи (рис. 2.40). 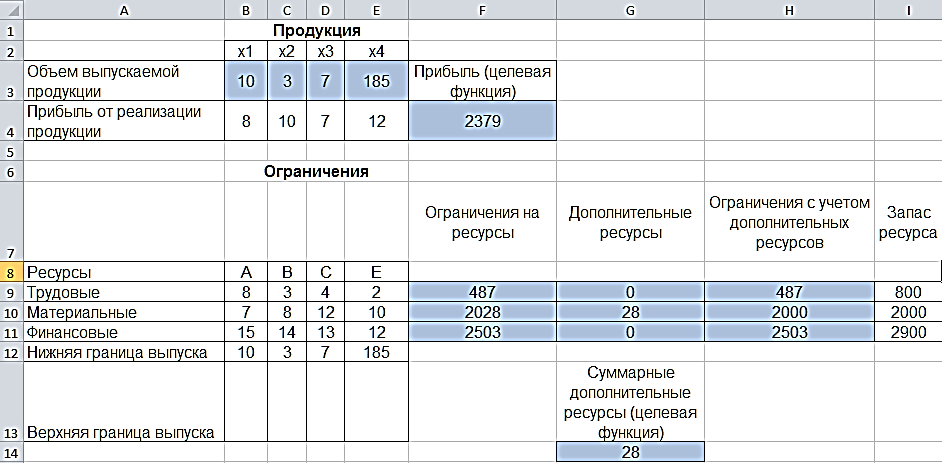 Рис. 2.40. Результат решения задачи 2 Результаты решения данной задачи показывают какого вида и сколько ресурсов потребуется для обеспечения выполнения скорректированного плана. Вся продукция выпускается на нижней границе. Трудовых и финансовых ресурсов достаточно для выполнения плана. Для материальных ресурсов требуется восполнение в объеме 28 единиц. Прибыль составит 2379 денежных единиц. Решение несбалансированной задачи, конечно, не заменило дополнительных ресурсов, но показало, что нужно для сбалансированного плана. Задания Задание 1 1. Решить задачи графическим методом, проверив на разрешимость. 2. Решить в Excel, используя «Поиск решения» и сравнить результаты. Примечания: Во всех задачах X1 0, X2 0.;  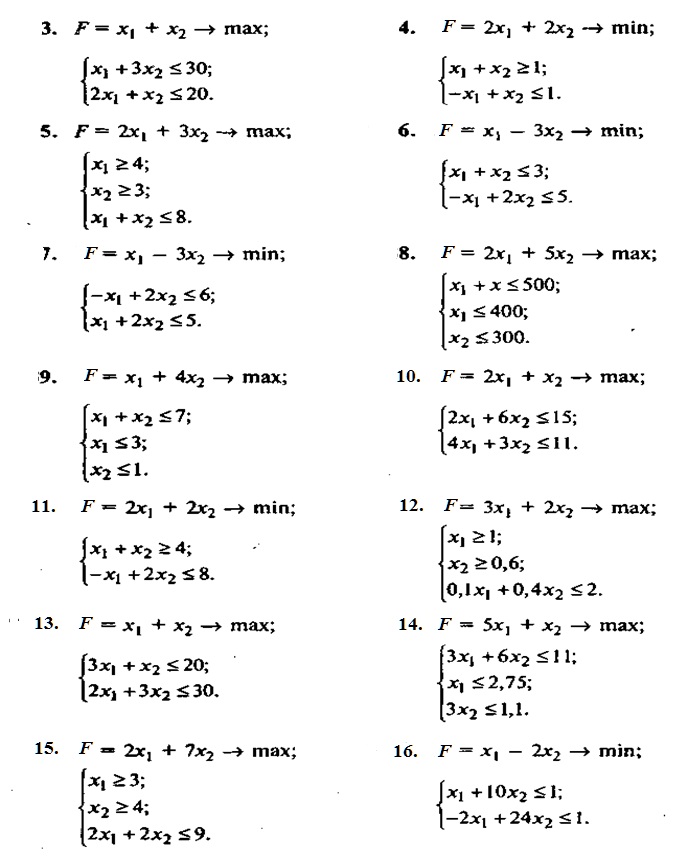  Задание 2 Построить математическую модель решения задачи. Решить задачу симплексным методом. Сделать выводы. Решить задачу в EXCEL. Сделать выводы. Сравнить результаты. Проделать пункты 2) и 3) с использованием дополнительных условий *. Вариант № 1 При производстве трех видов изделий Изд1, Изд2 и Изд3 предприятие использует четыре вида оборудования: сварочное, токарное, фрезерное и шлифовальное. Затраты времени на обработку каждого изделия и фонд рабочего времени каждого вида оборудования приведены в таблице.
Предприятие получает прибыль от реализации одного изделия Изд1 в размере 2 руб., от реализации одного изделия Изд2 - 3 руб., а от реализации одного изделия Изд3 - 1 руб. Определить, сколько изделий, и какого вида требуется изготовить предприятию, чтобы обеспечить максимальную прибыль от реализации. * Количество Изд3 должно быть не менее 5. Вариант № 2 На звероферме для обеспечения нормальных условий выращивания используется три вида кормов: Корм1, Корм2, Корм3 и Корм4. Количество единиц каждого вида корма, которое должны получать ежедневно звери, и ежедневные запасы кормов каждого вида приведены в таблице.
Прибыль от реализации одного Зверя1 составляет 35 руб., от реализации одного Зверя2 – 29 руб., от реализации одного Зверя3 – 39 руб., а от реализации одного Зверя4 – 52 руб. Определить, сколько зверей, и какого вида следует выращивать на звероферме, чтобы обеспечить максимальную прибыль от реализации. * Количество Зверя2 должно быть не менее 2. Вариант № 3 Из стандартных листов требуется вырезать заготовки четырех видов (Заготовка1, Заготовка2, Заготовка3, Заготовка4) в количествах, соответственно, не более 100, 60, 55 и 120 шт. Каждый лист может быть разрезан на заготовки несколькими способами. Количество получаемых заготовок при данном способе раскроя и прибыль от каждого вида раскроя приведены в таблице.
Определить сколько листов фанеры и по какому способу следует раскроить так, чтобы было получено нужное количество заготовок, обеспечивающее максимальную прибыль. * . Количество листов по 3-му способу должно быть не менее 1. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
