Решение одноиндексных оптимизационных задач. ЛР № 2. Решение одноиндексных оптимизационных задач Цель работы научиться решать одноиндексные оптимизационные задачи производства

• Название: Решение одноиндексных оптимизационных задач Цель работы научиться решать одноиндексные оптимизационные задачи производства
• Анкор: Решение одноиндексных оптимизационных задач
• Дата: 22.05.2023
• Размер: 4.38 Mb.
• Имя файла: ЛР № 2.docx
• Тип: Решение; #1151185
• страница: 7 из 8

Приложение 1.

Симплексный метод в решении задач с условием в виде уравнений и неравенств со знаком «≥» (метод искусственного базиса).

Ранее был рассмотрен основной алгоритм симплексного метода для решения так называемой стандартной задачи линейного программирования на максимум целевой функции, условие которой было представлено в виде неравенств с положительными свободными членами.

Исходные неравенства нами были преобразованы в уравнения путем ввода дополнительных неотрицательных неизвестных (x_n+1,…,х_п+т). Дополнительные неизвестные входили в симплексные уравнения со знаком плюс, и в единичной подматрице на главной диагонали мы имели элементы, равные единице. Это позволило нам получить исходную программу.

В целом ряде экономических задач исходные ограничительные условия могут быть представлены в виде уравнений или неравенств с любыми знаками: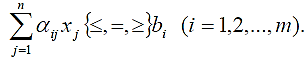



Предположим, дано условие задачи в виде системы линейных уравнений: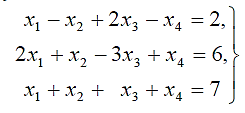

(2.4)

и требования минимизации целевой функции

F(x)=2x₁+x₂-x₃-x₄ (2.5)

при неотрицательных переменных x₁, x₂, x₃ и x₄ или то же в общем развернутом виде: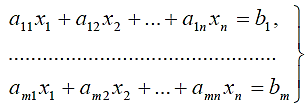

(2.6)

при bi≥0, i = l , 2, . . ., mи при x_j ≥0, j=1,2,…,nи минимизации целевой функции

F=c₁x₁ + c₂x₂+…+ c_nx_n. (2.7)

Как в числовом примере, так и в общей формулировке задачи нет таких переменных x_j, которые бы входили с коэффициентом + 1 один раз в какое-либо одно уравнение системы.

Следовательно, нет и явной исходной программы.

Рассмотрим еще один пример — раскройную задачу.

Условие задачи. Положим, что на мебельном комбинате производится раскрой ДСП на заготовки и детали для мебели. Известно, что из партии ДСП необходимо нарезать четыре вида (А, В,С,D)различных по размерам заготовок и деталей. Древесностружечная плита стандартных размеров может быть раскроена пятью способами (вариантами). По каждому возможному варианту раскроя составляется соответствующая карта раскроя. Из карт раскроя известен выход заготовок (в штуках) раз- ных размеров, а также площадь отходов при раскрое одной плиты по тому или иному варианту.

В задании на раскрой указано общее количество заготовок каждого вида, которые необходимо нарезать из партии плит, поступивших в раскрой. Все эти данные приведены в табл. 1.3.

Табл. 1.3

Виды (типоразмеры) заготовок и деталей	Задание на раскрой по выходу заготовок, шт.	Выход заготовок, шт., по видам, при раскрое одной плиты по вариантам
		1		2		3		4		5
А	500	0		0		1		1		0
В	1000	2		1		2		1		0
С	200	3		0		0		0		1
D	400	0		1		0		2		1
Площадь отходов, м2			0,5		0,6		0,4		0,2		0,3

В задаче требуется найти оптимальный план раскроя ДСП, обеспечивающий выход планового числа заготовок при минимальных суммарных отходах от раскроя всех плит. Иными словами, в задаче необходимо определить, сколько ДСП следует раскроить по тому или иному варианту раскроя, чтобы нарезать требуемое число заготовок и при этом отходы были бы минимальными.

Математическая модель задачи, заключающаяся в минимизации целевой функции

F=0,5x₁+0,6x₂+0,4x₃+0,2x₄+0,3x₅ (2.8)

при ограничениях, представленных в виде системы линейных неравенств: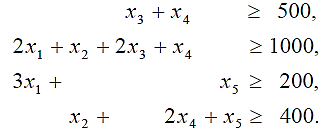

(2.9)

при x _j ≥0 (j =1,2,3,4,5)

или то же в общем виде

F=c₁x₁+ c₂x₂+…+ c_nx_n.= min (2.10)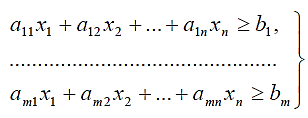

(2.11)

при x _j ≥0 ( j =1,2,..., n) и

при b_i ≥0 (i =1,2,..., m).

Эти исходные неравенства надо преобразовать в равенства с неотрицательными неизвестными. Для этого надо ввести дополнительные неотрицательные неизвестные х₆, x₇, х₈ и x₉ (а в общем случае x_n+1, х_п+2,…,х_п+т) в неравенства-ограничения так, чтобы они превратились в уравнения.

В данной задаче неравенства имеют противоположный смысл по сравнению с неравенствами, рассмотренными ранее, т. е. левые части должны быть не менее правых частей, поэтому дополнительные неотрицательные неизвестные должны вводиться со знаком плюс в правые части неравенств, либо со знаком минус (с коэффициентами -1) в левые части этих неравенств-ограничений.

Итак, вышеуказанные системы неравенств, преобразуются в следующие эквивалентные системы линейных уравнений: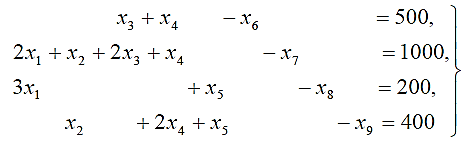

(2.12)

F=0,5x₁+0,6x₂+0,4x₃+0,2x₄+0,3x₅-0x₆-0x₇-0x₈-0x₉=min при x_j≥0 (2.13)

или, в общем виде,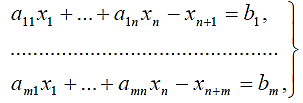

(2.14)

F=c₁x₁+…+ c_nx_n.+0x_n+1+…+0x_n+m= min. (2.15)

В матрицах систем уравнений такого вида не содержится единичной подматрицы, в которой диагональные элементы были бы равны единице, а остальные - нулю. В них содержатся подматрицы, соответствующие дополнительным неизвестным, с диагональными элементами, равными -1. Поэтому, если принять дополнительные неизвестные в качестве базисных, то они окажутся отрицательными (х₁ = х₂ = х₃ = х₄ = x₅ = 0, х₆= -500, х₇ = -1000, х₈ = -200, x₉ = -400), т. е. не будут удовлетворять условиям неотрицательности всех переменных. Следовательно, здесь мы не имеем явной неотрицательной исходной программы.

Для решения задачи необходима единичная подматрица (с положительными элементами). Чтобы получить ее, надо ввести еще одну группу неизвестных, число которых равно числу исходных неравенств (или уравнений), по одному такому неизвестному на каждое неравенство (или уравнение). Эти новые неизвестные в отличие от дополнительных - уравновешивающих — называют