Решение одноиндексных оптимизационных задач. ЛР № 2. Решение одноиндексных оптимизационных задач Цель работы научиться решать одноиндексные оптимизационные задачи производства
 Скачать 4.38 Mb.
|
|
Элементы целевой строки таблицы не соответствуют условию оптимальности, так как среди них имеются отрицательные величины. Это свидетельствует о возможности увеличения целевой функции, следовательно, опорное решение, не является оптимальным. То обстоятельство, что базисными сейчас являются дополнительные переменные, означает, что никакая проду/кция не производится и все имеющиеся ресурсы не используются. Переход к новому опорному плану Поскольку проверяемое решение не является оптимальным, найдем другое опорное решение, «улучшающее» значение целевой функции. Это возможно только в том случае, если возрастание какой-либо свободной (нулевой) переменной (х1 или х2) ведет к улучшению значения целевой функции. Но для того, чтобы свободная переменная стала положительной (перешла в число базисных переменных), надо одну из текущих базисных переменных сделать нулевой, т.е. перевести в разряд свободных. Это необходимо, чтобы новое решение содержало в точности m базисных переменных. Таким образом, переход к новому опорному плану осуществляется путем замены базисных переменных. При этом выбранная для ввода в число базисных свободная переменная называется вводимой, а удаляемая в разряд свободных базисная переменная – выводимой. Выбор вводимой в число базисных переменной определяется условием оптимальности F≥0: вводимая в число базисных переменная определяется максимальной по абсолютной величине отрицательной оценкой при решении задачи на максимум целевой функции и наибольшей положительной оценкой – при решении задачи на минимум. Соответствующий столбец коэффициентов в симплекс-таблице будем называть ключевым (S). В нашем случае это столбец х2, в котором F=-3. Для определения ключевой строки (q), рассчитаем оценочные отношения (табл. 2.2). Из полученных значений следует выбрать минимальное. Такое значение определится из следующего соотношения: 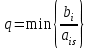 .Таблица 2.2 – Первый шаг. Определение ключевого элемента
 Наименьшим числом среди оценочных отношений является 5, поэтому третья строка будет разрешающей. Выделим её в таблице и запомним её номер полагая q=3. На пересечении разрешающего столбца и разрешающей строки находится разрешающий элемент а32=1.Строим таблицу 2.3 следующим образом: Таблица 2.3 - Второй шаг
а) в первом столбце базисную переменную x5, находящуюся в разрешающей строке, заменим переменной x2, расположенной в разрешающем столбце; б) расставляем нули и единицы в столбцах, которые соответствуют базисным переменным: ставим единицу, если клетка на пересечении столбца и строки с базисными переменными с одинаковым индексоми ноль - если с разными индексами. Элементы строки с номером q=3 получаем делением каждого элемента разрешающей строки таблицы 1 на разрешающий элемент а32=1; Остальные клетк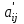и  и 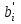 заполняем по правилу прямоугольника. Вершины прямоугольника выбираем следующим образом (рис. 2.9):  Рис. 2.9. Правило прямоугольника - одна из вершин - клетка (i,j), - по диагонали с ней расположена клетка с разрешающим элементом (q,s); - третья клетка находится на пересечении строки i и разрешающего столбца, т. е. клетка (i,s); - четвёртая клетка находится на пересечении столбца j и разрешающей строки, т.е. клетка (q,j). 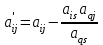 ;  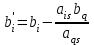В итоге получим таблицу 2.3.  Критерий оптимальности в таблице 2.3 не выполнен. Разрешающим будет столбец 1, а разрешающей строкой - строка 1. Разрешающий элемент  . 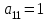Построим новую таблицу 2.4.Таблица 2.4 - Третий шаг
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||