Решение одноиндексных оптимизационных задач. ЛР № 2. Решение одноиндексных оптимизационных задач Цель работы научиться решать одноиндексные оптимизационные задачи производства

• Название: Решение одноиндексных оптимизационных задач Цель работы научиться решать одноиндексные оптимизационные задачи производства
• Анкор: Решение одноиндексных оптимизационных задач
• Дата: 22.05.2023
• Размер: 4.38 Mb.
• Имя файла: ЛР № 2.docx
• Тип: Решение; #1151185
• страница: 4 из 8

Критерий оптимальности в таблице 3 не выполнен. Разрешающим будет столбец 5, а разрешающей строкой - строка 2. Разрешающий элемент 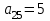. Построим новую таблицу 2.5.
Таблица 2.5 - Четвертый шаг

Базис	Свободный член, bi	Переменные							Оценочные отношения
		x1	x2	x3	x4	x5	x6
x1	6	1	0	-0,2	0,6	0	0
x5	1	0	0	-0,4	0,2	1	0
x2	4	0	1	0,4	-0,2	0	0
x6	3	0	0	0,6	-1,8	0	1
F	24	0	0	0,8	0,6	0	0

Критерий оптимальности в таблице 4 выполнен. Целевая функция F_max=24 достигается при X=(6;4;0;0;1;3).

Оптимальное решение задачи линейного программирования можно "считать" из симплекс-таблицы следующим образом. Неотрицательные (базисные) переменные представлены в столбце "Базис", а их значения — в столбце " Свободный член, b_i ". В данном примере имеем следующее:

1. 
   ежедневно следует производить 6 ед. краски х1;
   
2. 
   ежедневно следует производить 4 ед. краски х2;
   
3. 
   ежедневный доход составляет 24 у.е.
   

С помощью симплекс-таблицы можно получить много дополнительной информации (кроме непосредственно оптимального решения).

1. Состояние ресурсов.

2. Цена единицы ресурсов (двойственные цены).

3. Все данные, необходимые для проведения анализа чувствительности оптимального решения.

Покажем, как определить состояние (статус) ресурсов. Статус ресурса определяется как дефицитный или недефицитный, в зависимости от того, будет он использован полностью или нет. Эту информацию можно получить из результирующей симплекс-таблицы путем проверки значений дополнительных (остаточных) переменных, ассоциируемых с соответствующими ограничениями, накладываемыми на ресурсы.

Если дополнительная переменная равна нулю, значит, ресурс использован полностью, и он получает статус дефицитного.

Положительное значение дополнительной переменной указывает на недефицитность соответствующего ресурса. В нашем случае мы имеем дефицит сырья М1 и М2, т.к оно используется полностью при х1=6 и х2=4.

Переменные х5=1 ед. и х6=3 ед. говорят о том, что при наличии достаточного сырья из-за неполного удовлетворения потребностей изданий, можно было бы увеличить выпуск краски х1 на 1 ед., а краски х2 – на 3 ед.

Решение задач линейногопрограммирования с использованием MS EXCEL

Общий алгоритм решения

Как отмечалось выше, в качестве инструмента решения оптимизационных задач используется математическое программирование.

Математическое программирование представляет собой математическую дисциплину, занимающуюся изучением экстремальных задач и разработкой методов их решения.

В общем виде математическая постановка экстремальной задачи состоит в определении наибольшего или наименьшего значения целевой функция F(х₁, х₂, ..., х_n) при условиях а_i(х₁, x₂, ..., х_n) ≤b_i, (і= 1 ^{̅̅̅ ̅ ̅̅}m), где F и a_i заданные функции, а b_i – некоторые действительные числа.

В зависимости от свойств функций F и a_i математическое программирование можно рассматривать как ряд самостоятельных дисциплин, занимающихся изучением и разработкой методов решения определенных классов задач.

Прежде всего, задачи математического программирования делятся на задачи линейного и нелинейного программирования. При этом если все функции F и а_i, линейные, то соответствующая задача является задачей линейного программирования. Если же хотя бы одна из указанных функций нелинейная, то соответствующая задача является задачей нелинейного программирования.

Для решения задач оптимизации в MS Excel 2010 используется инструмент «Поиск решения».

Общий алгоритм решения оптимизационных задач в MS Excel 2010 следующий:

1. 
   Составить математическую модель.
   
2. 
   Ввести на рабочий лист Excel условия задачи:
   

а) создать таблицу на рабочем листе для ввода условий задачи;

б) ввести исходные данные, целевую функцию, ограничения и граничные условия.

3. 
   Выполнить команду «Данные – Анализ - Поиск решения».
   
4. 
   Указать параметры в диалоговом окне «Параметры поиска решения», выполнить решение.
   
5. 
   Проанализировать полученные результаты.
   

Настройка доступа к инструменту Поиск решения

Доступ к инструменту Поиск решения осуществляется с помощью команды Данные Анализ Поиск решения (рис. 2.10).



Рис. 2.10. Режим «Поиск решения»

Если команда «Поиск решения» или группа «Анализ» отсутствует на вкладке «Данные», то необходимо загрузить соответствующую надстройку:

1. 
   Выбрать команду «Файл – Параметры».
   
2. 
   В диалоговом окне «Параметры» Ехсеl выбрать категорию «Надстройки»(рис. 2.12).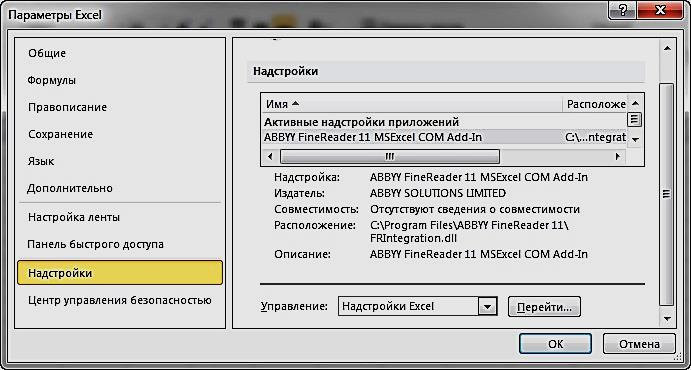
   

Рис. 2.12. Окно «Параметры»

3. 
   В поле «Управление» выбрать значение «Надстройки Excel», затем кнопку «Перейти».
   
4. 
   В поле «Доступные надстройки» установить флажок рядом с пунктом «Поиск решения» (рис. 2.13) и нажать кнопку ОК.
   

После выполнения этих действий команда Поиск решения будет доступной в группе команд Анализ вкладки Данные (рис. 2.10).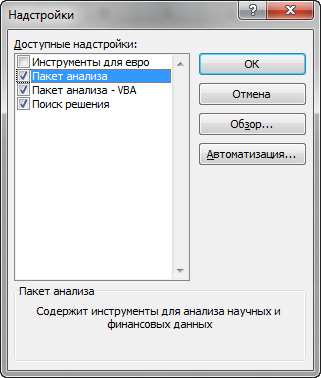



Рис. 2.13. Окно «Надстройки»

Параметры инструмента Поиск решения

Как отмечалось ранее, доступ к инструменту «Поиск решения» осуществляется с помощью команды «Данные – Анализ - Поиск решения» (рис. 2.14).

Данная команда отображает окно диалога «Параметры поиска решения». Перед использованием рассматриваемого инструмента на листе электронной таблицы должны быть сформированы целевая функция, область изменяемых ячеек (неизвестные), значения которых будут найдены в процессе решения. Решение (изменяемые ячейки) должно находиться в определенных пределах или удовлетворять определенным ограничениям.

Параметры задачи ограничиваются такими предельными показателями:

• 
  количество неизвестных – 200;
  
• 
  количество формульных ограничений на неизвестные – 100;
  
• 
  количество предельных условий на неизвестные – 400.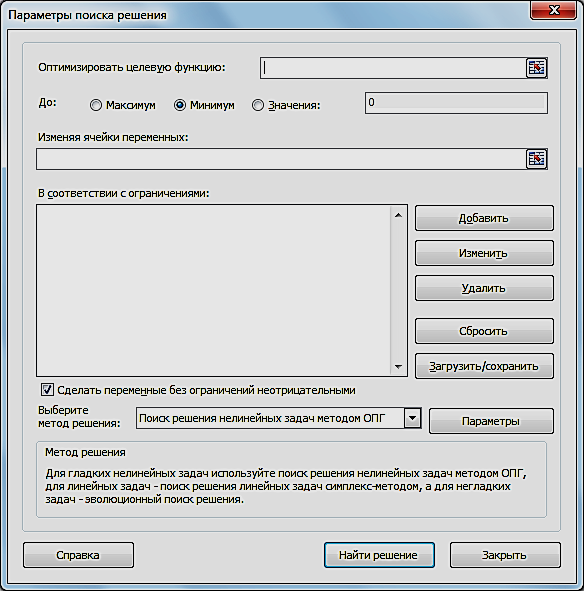
  

Рис. 2.14. Окно «параметры поиска решения»

В окне диалога «Параметры поиска решения» в поле «Оптимизировать целевую функцию» указывается адрес ячейки с целевой функцией. Целевая функция зависит от изменяемых ячеек и связана с ними некоторой формулой. Оптимизируется значение целевой функции до максимума, минимума, или некоторого определенного значения.

В поле «Изменяя ячейки переменных» указывается адрес блока ячеек, которые и будут решением.

В область «В соответствии с ограничениями» вводятся ограничения на решение. Кнопки «Добавить, Изменить, Удалить» управляют ограничениями, их действия интуитивно понятны.

Если в пределах одного рабочего листа Excel необходимо рассмотреть несколько моделей оптимизации (например, найти максимум и минимум одной функции или максимальные значения нескольких функций), то удобнее сохранить эти модели, используя кнопку «Загрузить/сохранить». Диапазон для сохраняемой модели содержит информацию о целевой ячейке, об изменяемых ячейках, о каждом из ограничений и все значения окна диалога «Параметры». Выбор сохраненной ранее модели для решения конкретной оптимизационной задачи осуществляется также с помощью кнопки «Загрузить/сохранить».

Флажок в поле «Сделать переменные без ограничений неотрицательными» позволяет не вводить дополнительно ограничения на изменяемые ячейки, если их значения неотрицательны.

Поиск решения в зависимости от типа решаемых задач, позволяет использовать методы:

• 
  Симплексный метод.
  
• 
  Метод ОПГ (обобщенного приведенного градиента).
  
• 
  Эволюционный поиск решения.
  

Метод решения выбирается из раскрывающегося списка «Выберите метод решения» рассматриваемого окна диалога.

Кнопка «Найти решение» запускает процесс решения задачи.

Иногда, в результате выполнения процедуры поиска решения, само решение не находится, даже если известно, что решение существует. Часто эту проблему удается решить, изменив некоторые параметры и повторно запустив «Поиск решения». Указанные параметры устанавливаются в диалоговом окне «Параметры» (рис. 2.15), которое отобразится, если в окне диалога «Параметры поиска решения» выбрать кнопку «Параметры».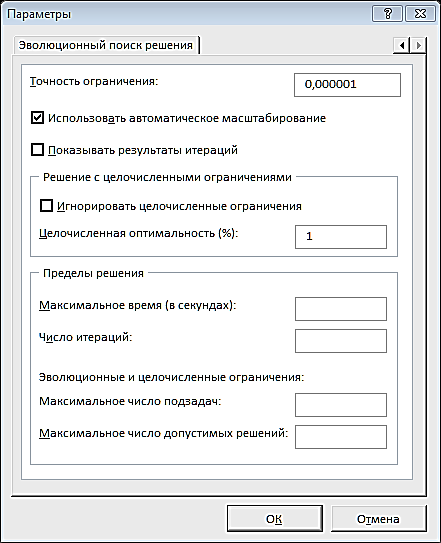



Рис. 2.15. Окно «Параметры»

Ниже описаны основные параметры вкладки.

Точность ограничения. Указывает насколько точно выполняются ограничения. Задача может быть решена быстрее, если задать меньшую точность.

Использовать автоматическое масштабирование. Служит для автоматической нормализации входных и выходных значений, значительно различающихся по величине.

Показывать результаты итераций. Если этот параметр активизирован, то после выполнения очередной итерации решение приостанавливается, и отображаются найденные результаты.

Игнорировать целочисленные ограничения. При установке этого параметра игнорируются ограничения, определяющие, что значения должны быть целыми. Применение этого параметра иногда позволяет найти решение, которое в противном случае обнаружить нельзя.

Максимальное время. Предоставляет возможность ограничить максимальное время решения задачи (в секундах). Если появится сообщение, что время на решение задачи истекло, то его можно добавить.

Число итераций. Используется для ввода максимального числа промежуточных решений, допустимых при поиске решения.

Максимальное число подзадач. Параметр предназначен для решения сложных задач. Позволяет задать максимальное количество подзадач, которые могут использоваться при применении эволюционного алгоритма.

Максимальное число допустимых решений. Параметр предназначен для решения сложных задач. Позволяет задать максимальное количество приемлемых решений, которые могут использоваться при применении эволюционного алгоритма.

Пример решения задач линейного программирования.

Задача определения оптимального ассортиментапродукции

Предприятие изготавливает четыре вида продукции – A, B, C и D. Для производства продукции используются ресурсы – трудовые, материальные, финансовые. Максимальный запас ресурсов на производстве 800, 2000, 2900 соответственно. Расход ресурсов на единицу производства продукции A, B, C и D и предельно допустимые значения выпуска каждого вида даны в табл. 2.6.

Таблица 2.6. Условие задачи 1

Ресурсы	Расход ресурса на единицу продукции					Запас ресурса
	A	B	C	D
Трудовые	8	3	4	4	800
Материальные	7	8	12	10	2000
Финансовые	15	14	13	14	2900
Нижняя граница выпуска	12		3
Верхняя граница выпуска	30	25

Прибыль от реализации единицы продукции равны: 8 д. е. – для A, 10 д. е. – для B, 7 д. е. – для C, 8 д. е. – для D.

Какой объем продукции каждого вида должно производить предприятие, чтобы прибыль от реализации продукции была максимальной?

Решение.Составим математическую модель для решения поставленной задачи.

Обозначим переменные:

x₁ – объем произведенной продукции вида А; x₂ – объем произведенной продукции вида B; x₃ – объем произведенной продукции вида C; x₄ – объем произведенной продукции вида D;

Поскольку производство продукции ограничено имеющимися в распоряжении предприятия ресурсами и спросом на данную продукцию, а также учитывая, что объем изготовляемой продукции не может быть отрицательным, должны выполняться следующие неравенства: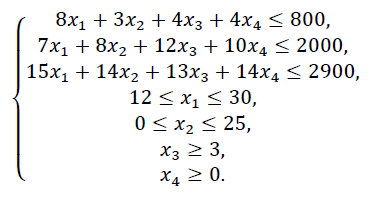



Прибыль от реализации продукции составит:



Cреди всех неотрицательных решений системы линейных неравенств требуется найти такое, при котором функция F принимает максимальное значение F_max.

Рассматриваемая задача относится к разряду типовых задач оптимизации производственной программы предприятия. В качестве критериев оптимальности в этих задачах могут быть также использованы прибыль, себестоимость, номенклатура производимой продукции, затраты станочного времени и др.

Создадим на рабочем листе таблицу для ввода исходных данных (рис. 2.16). Заливкой выделены ячейки для ввода формул и вывода результата.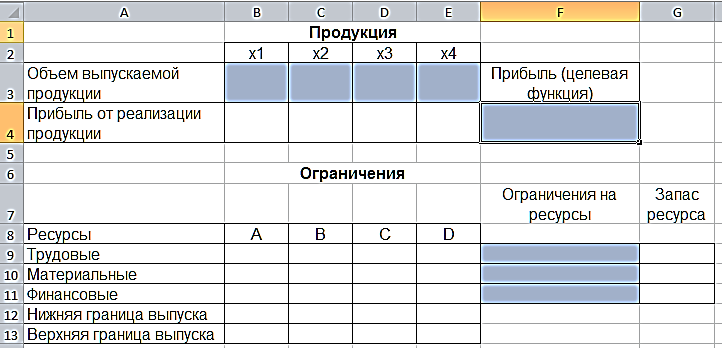



Рис. 2.16. Экранная форма задачи

Заполним таблицу.

Блок ячеек В3:Е3 содержит оптимальное решение, значение этих ячеек будет получено в результате решения задачи.

Блок ячеек В4:Е4 содержит значения прибыли от реализации продукции. В ячейках В9: Е13 отображен расход ресурсов на единицу производства продукции A, B, C и D и предельно допустимые значения выпуска каждого вида.

Для вычисления целевой функции в ячейке F4 используем функцию =СУММПРОИЗВ($B$3:$E$3;B4:E4) (рис. 2.17).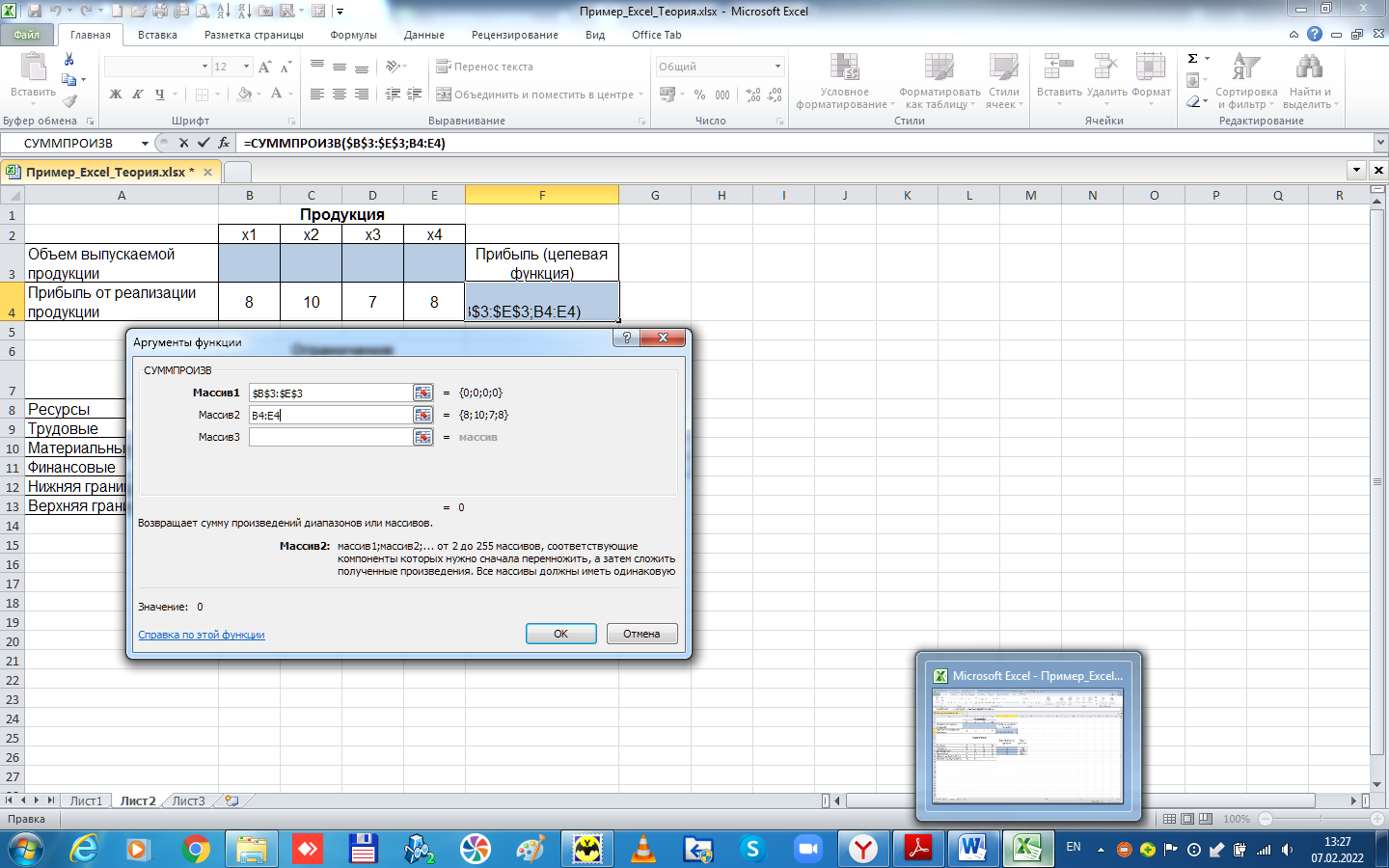



Рис. 2.17. Функция СУММПРОИЗВ

В ячейки F9:F11 введены формулы для расчета ограничений по ресурсам. На рис. 2.18 представлена таблица с исходными данными, целевой функцией, ограничениями и граничными условиями.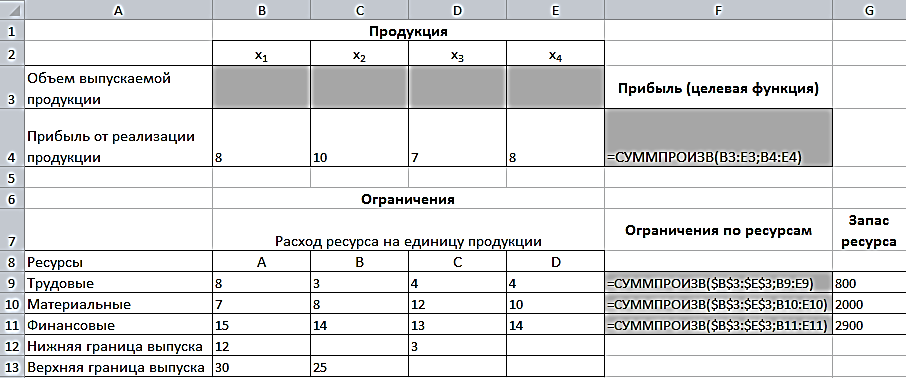



Рис. 2.18. Исходные данные с формулами

На вкладке «Данные» в группе «Анализ» выберем команду Поиск решения.

На экране отобразится диалоговое окно «Параметры поиска решения», в котором установим следующие параметры (рис. 2.19):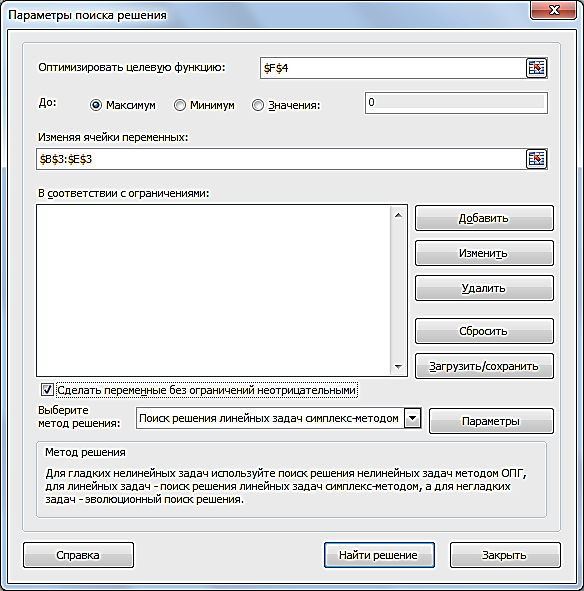



Рис. 2.19. Окно «Параметры поиска решения»

• 
  в поле «Оптимизировать целевую функцию» указываем адрес ячейки со значением целевой функции – F4;
  
• 
  выбираем нахождение максимума целевой функции;
  
• 
  в поле «Изменяя ячейки переменных» указываем адреса ячеек со значениями искомых переменных B3:Е3;
  
• 
  в области «В соответствии с ограничениями» с помощью кнопки «Добавить» размещаем все ограничения задачи (добавление ограничений будет рассмотрено ниже);
  
• 
  установим флажок в поле «Сделать переменные без ограничений неотрицательными»;
  
• 
  в списке «Выберите метод решения» указываем «Поиск решения линейных задач симплекс-методом»;
  
• 
  нажимаем кнопку «Найти решение»
  

Остановимся подробно на добавлении ограничений в область В соответствии с ограничениями.

Все ограничения указаны в математической модели задачи. Для добавления ограничения необходимо выбрать кнопку «Добавить». Отобразится окно диалога «Добавление ограничений» (Рис. 2.20).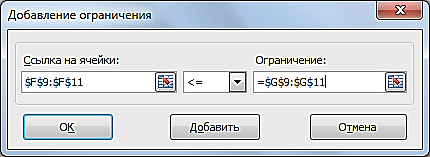



Рис. 2.20. Окно «Добавление ограничений»

Добавляем ограничения для неравенств: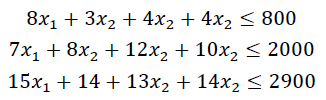



В поле «Ссылка на ячейки» указываем адрес диапазона F9:F11, выбираем в раскрывающемся списке знак неравенства ≤, в поле Ограничение выделяем диапазон G9:G11 и нажимаем кнопку «Добавить». Результатом этого действия будет добавление текущего ограничения в список ограничений, поля окна Добавление ограничения будут очищены для ввода следующего ограничения.

Порядок ввода ограничений не имеет значения. Главное — не забыть ни одно из ограничений.

Покажем окна для добавления остальных ограничений.

х1≤12≤30 (рис. 2.21, 2.22).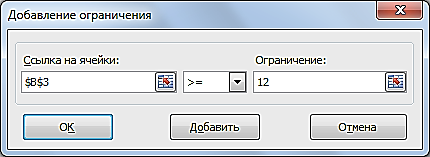



Рис. 2.21. Добавление левой части ограничения по х1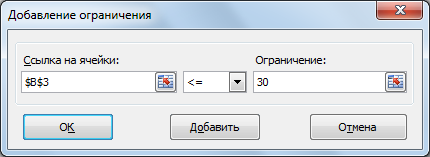



Рис. 2.22. Добавление правой части ограничения по х1

х2≤25 - (рис. 2.23).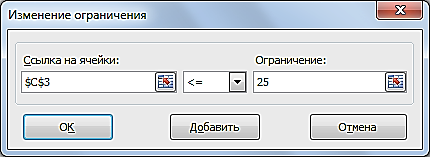



Рис. 2.23. Добавление ограничения по х2

х3≥25 - (рис. 2.24).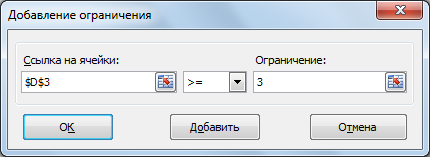



Рис. 2.24. Добавление ограничения по х3

Ограничения х2≥0 и х4≥0 можно не добавлять, т.к. в окне «Параметры поиска решения» установлен флажок в поле «Сделать переменные без ограничений неотрицательными».

Для принятия последнего ограничения и возврата к диалоговому окну «Параметры поиска решения» нажмем кнопку OK.

После указания всех необходимых параметров в диалоговое окно Параметры поиска решения примет вид (рис. 2.25):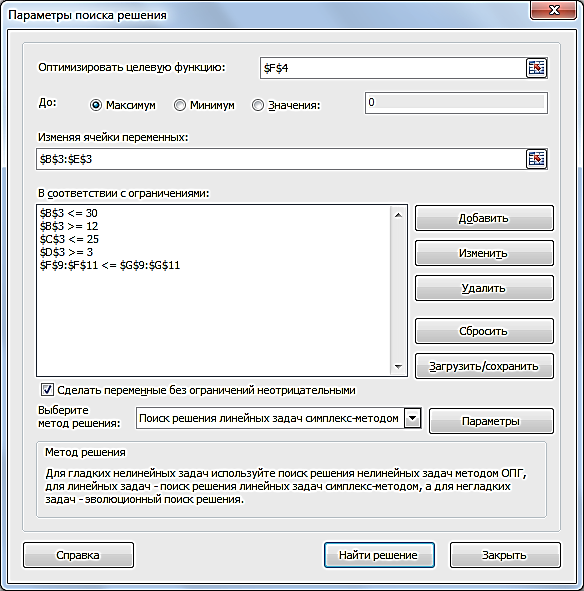



Рис. 2.25. Окно «Параметры поиска решения» с ограничениями

После нажатия кнопки «Найти решение» отобразится окно «Результаты поиска решения» (рис. 2.26).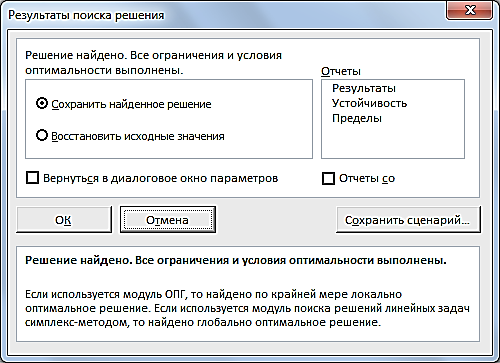



Рис. 2.26. Окно «Результаты поиска решения»

Для сохранения полученного решения необходимо установить переключатель «Сохранить найденное решение» и нажать кнопку ОК. После чего на рабочем листе отобразится решение задачи (рис. 2.27).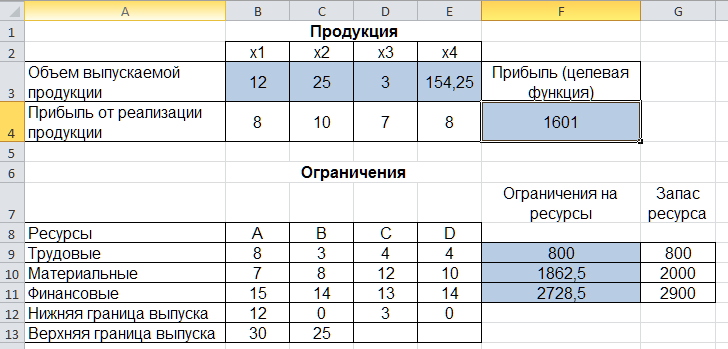



Рис. 2.27. Результаты решения задачи

Таким образом, максимальная прибыль при реализации продукции будет получена в размере 1601 д. е. при следующем плане производства:

• 
  12,00 – объем продукции типа А;
  
• 
  25,00 – объем продукции типа B;
  
• 
  3,00 – объем продукции типа C;
  
• 
  154,25– объем продукции типа D.
  

Кроме вставки оптимальных значений в изменяемые ячейки, «Поиск решения» позволяет представлять результаты в виде трех отчетов: «Результаты, Устойчивость и Пределы». Для генерации одного или нескольких отчетов необходимо выделить их названия в окне диалога «Результаты поиска решения» (рис. 2.26). Для выбора нескольких отчетов из списка использовать клавишу Shift.

Рассмотрим более подробно каждый из них.

Отчет по результатам (рис. 2.28) содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления и окончательное значение, во второй – значения искомых переменных: исходные и полученные в результате решения задачи, в третьей – результаты оптимального решения для ограничений.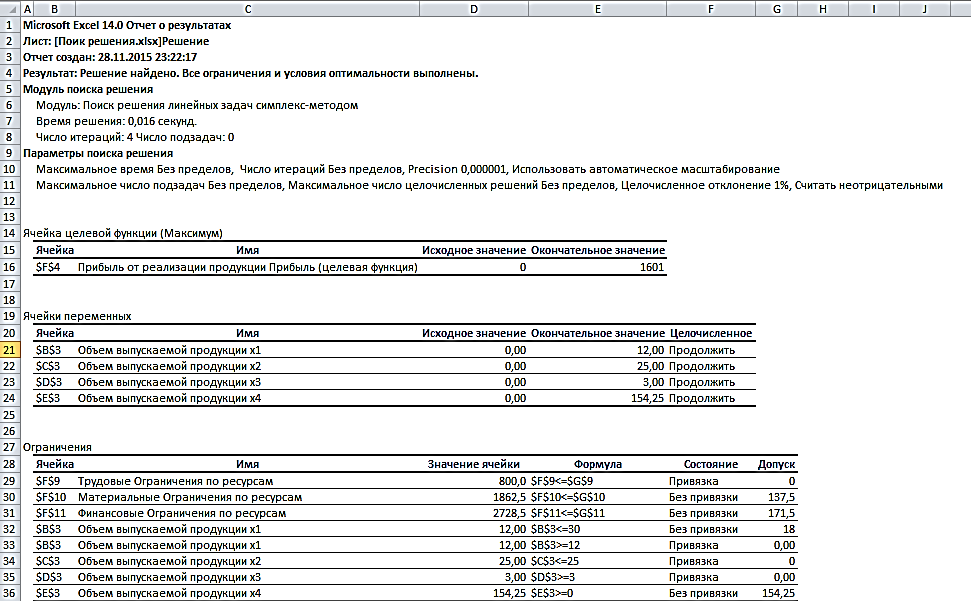



Рис. 2.28. Отчет о результатах

Этот отчет также содержит информацию о таких параметрах каждого ограничения, как состояние и допуск. Состояние принимает значение «Привязка», если вводимые ограничения совпадают с ограничениями, полученными в результате вычислений, и значение «Без привязки» в противном случае.

По значениям столбца «Допуск» можно сделать вывод о недоиспользованных ресурсах. В рассматриваемой задаче трудовые ресурсы были использованы полностью (значение в столбце «Допуск» равно 0), материальные ресурсы использованы не полностью (недоиспользованными оказались 137,5 единиц), также недоиспользовано 171,5 ед. финансовых ресурсов.

Отчет по устойчивости (рис. 2.29) содержит два блока: Ячейки переменных и Ограничения. Первый блок содержит информацию по допустимому увеличению и уменьшению коэффициентов целевой функции при условии, что объем оптимальной продукции не изменится. Второй блок касается увеличения и уменьшения значений ограничений.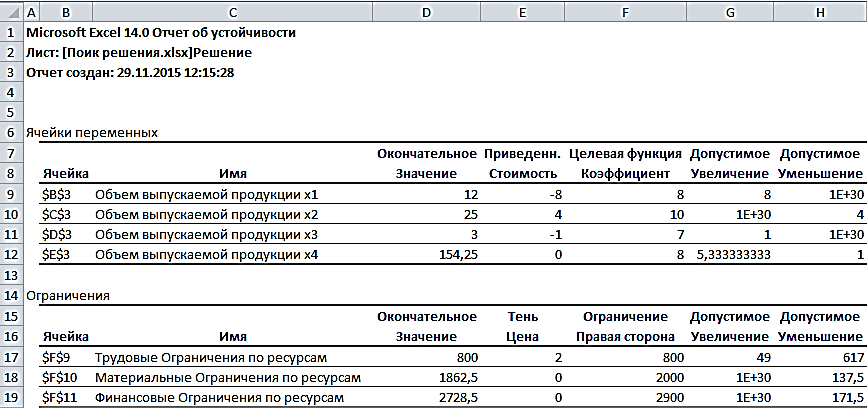



Рис. 2.29. Отчет по устойчивости

Отчет по пределам (рис. 2.30) содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи. Для каждой изменяемой ячейки этот отчет содержит оптимальное значение, а также наименьшие значения, которые ячейка может принимать без нарушения ограничений.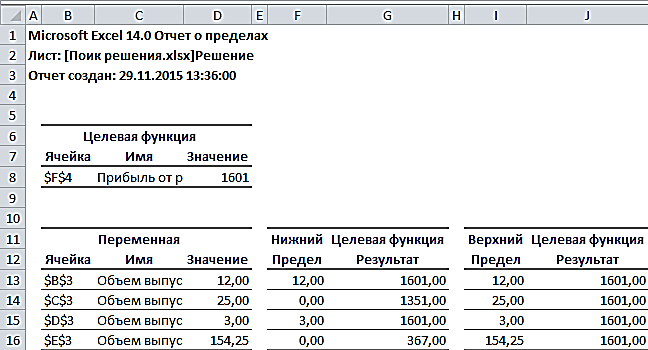



Рис. 2.30. Отчет о пределах

При сохранении книги Excel после выполнения поиска решения все значения, введенные в окнах диалога «Поиск решения», сохраняются вместе с данными рабочего листа. С каждым рабочим листом в рабочей книге можно сохранить один набор значений параметров «Поиска решения».

Кнопка «Сохранить сценарий» окна «Результаты поиска решения» (рис. 2.31) позволяет сохранить сценарий текущей модели. Все сценарии доступны в «Диспетчере сценариев», который открывается командой «Данные - Работа с данными - Анализ что-если - Диспетчер сценариев».