Решение одноиндексных оптимизационных задач. ЛР № 2. Решение одноиндексных оптимизационных задач Цель работы научиться решать одноиндексные оптимизационные задачи производства
 Скачать 4.38 Mb. Скачать 4.38 Mb.
|
|
искусственными. В данной задаче обозначим их через y1, у2, у3, y4 и введем их в левые части уравнений со знаком плюс. Симплексные уравнения исходных условий в окончательном виде, допускающем перенесение коэффициентов при неизвестных непосредственно в первоначальную симплекcную таблицу, будут1: 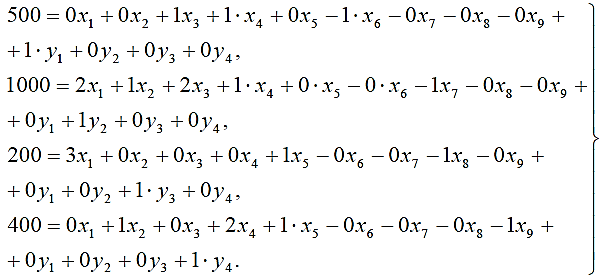 (2.16) (2.16)В этих уравнениях имеется единичная подматрица и все неизвестные считаются неотрицательными. Дальнейшее решение задачи может быть выполнено двумя способами. Первый способ заключается в отыскании какой-то программы (опорного плана) основной задачи (2.8), (2.9) посредством решения вспомогательной задачи,которая заключается в нахождении минимума целевой функции: F’=y1+ y2+ y3+y4=min (2.17) или, в расширенном виде, F’=0x1+0x2+0x3+0x4+0x5+0x6+0x7+0x8+0x9+1y1+1y2+1y3+1y4=min Если получится минимум этой целевой функции, равный нулю (F' = 0), то в решении этой вспомогательной задачи (3.24; 3.25) получится искомая программа исходной задачи (3.16; 3.17). Второй способ решения этой задачи. Он в значительной мере отличается от первого хотя бы тем, что здесь не требуется решать вспомогательную задачу для отыскания опорного плана (какого-то решения) исходной задачи. Этот способ позволяет нам приступить к непосредственному решению исходной задачи, поскольку в симплексных уравнениях, представленных в окончательной форме, имеется единичная подматрица (2.16). Целевая функция была представлена выражением (2.8): F=0,5x1+0,6x2+0,4xз+0,2x4+0,3x5=min Искусственные переменные у1, y2, y3 и y4 входят в первоначальную программу, с которой начинается процесс решения задачи, как базисные с положительными значениями, но по ходу решения они постепенно исключаются из базисных переменных. Оптимальной программа станет не раньше, чем все эти искусственные переменные перейдут из базисных в свободные. Чтобы это обеспечить, искусственные неизвестные вводятся в уравнение целевой функции с коэффициентами (ценами), равными М. Под Мпонимается величина больше любого другого сколько угодно большего наперед заданного числа. Таким образом, мы блокируем искусственные неизвестные, т. е. введением коэффициентов Ммы избавляемся от влияния искусственных переменных на истинную оптимальную программу. Действительно, как только хотя бы одна из искусственных переменных в программе положительна, значение целевой функции расширенной задачи (с искусственными переменными), соответствующим подбором положительного числа М, может быть сделано больше любого значения целевой функции (2.8) исходной задачи при любых значениях основных переменных х1, x2, x3, x4, х5. Следовательно, минимум целевой функции может быть получен только при нулевых значениях искусственных переменных. Целевая функция нашей задачи примет следующее выражение: F= 0,5x1 + 0,6x2 + 0,4x3 + 0,2x4 + 0,3x5-0x6-0x7-0x8 -0 x9+My1+ My2+ My3+ My4 = min Теперь все готово для решения задачи. Можно приступить к составлению первой симплексной рис. (2.41), которая будет иметь точно такой же вид, как и в задачах, рассмотренных ранее. 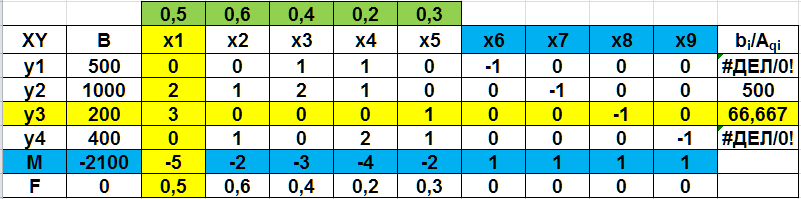 Рис. 2.41. Первая симплекс-таблица В первоначальную программу войдут все искусственные переменные. Однако есть и некоторая особенность таблицы, заключающаяся в том, что в задачу входит неопределенное число М. Строка М формируется как отрицательная сумма предыдущих строк: столбец В - 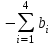 ; столбцы х1–х9 - ; столбцы х1–х9 - 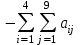 . .Далее выбираем разрешающий столбец, но поскольку задача решается на минимум, в строке F выбираем положительные элементы, а строке М – максимальный по модулю отрицательный элемент (за исключением столбца В). Таким образом выбран столбец 1 (х1). Далее, оцениваем отношения элементов столбца В к элементам разрешающего столбца (bi/Aqi), и выбираем большее положительное значение (строка 3 – y3). После этого по аналогичному алгоритму, рассмотренному ранее, пересчитываем вторую таблицу (рис. 2.42) 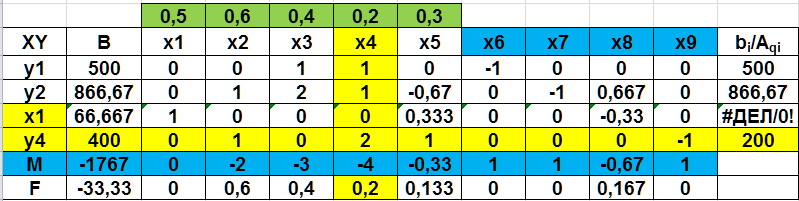 Рис. 2.42 Вторая симплекс-таблица В этой таблице разрешающий столбец – 4 (х4), а разрешающая строка – 4 (y4). Переходим к расчету третьей и т.д. таблицам (рис. 2.43-2.45). 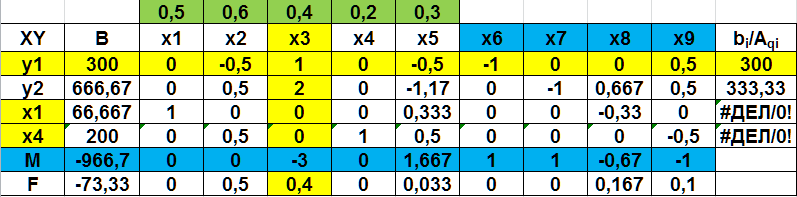 Рис. 2.43 Третья симплекс-таблица 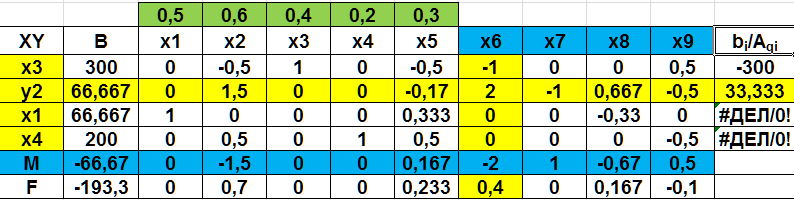 Рис. 2.44 Четвертая симплекс-таблица На пятой итерации (рис. 2.45) получаем в строке М все нули, а все искусственные переменные y1- y4 замещены на основные и базисные переменные х. 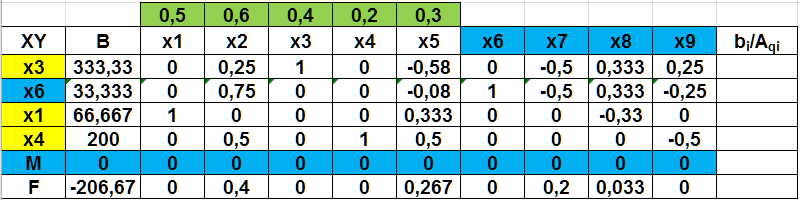 Рис. 2.45 Пятая симплекс-таблица Следовательно, получаем оптимальное решение F-206,67=0, или F=206,67, при х1=66,667, х3=333,33, х4=200. Значение х6=33,33 показывает насколько первое ограничение превышает значение ресурса 500. |
