Решение по действиям с пояснениями и выражением. Желательно рассмотреть два способа решения задачи
 Скачать 1.5 Mb. Скачать 1.5 Mb.
|
|
VII. Решение выражений. С подробным объяснением на доске выполняется задание 1 (с. 27 учебника, часть 2), а затем самостоятельно ученики выполняют задание 6 (с. 27 учебника, часть 2), в котором, после того как найдут значение выражения, делают проверку. Самопроверка. VIII. Работа с геометрическим материалом. – Рассмотрите фигуры, изображённые на полях с. 27 (учебник, часть 2). – Что хотите сказать? – Какая из этих фигур лишняя? (Лишними могут быть: фигура 2, так как это треугольник, а все остальные фигуры – четырёхугольники; фигура 1, так как в ней нет прямых углов, а в остальных фигурах есть; фигура 3, так как она зелёного цвета, а все остальные фигуры – розового.) IX. Итог урока. – Что хотите сказать? – Что особенно понравилось? Запомнилось? – Оцените свою работу на уроке. У р о к 87. ПРЯМОУГОЛЬНИК Цели: расширять представления учащихся о прямоугольнике как о четырёхугольнике, у которого все углы прямые и противоположные стороны равны; закреплять умение учеников решать задачи изученных видов; продолжать формировать умение учащихся применять на практике изученные приёмы письменного сложения и вычитания. Ход урока I. Организационный момент. II. Каллиграфическая минутка. 48 48 48 48 48 84 84 84 84 84 III. Устный счёт. 1. b = 64, 43, 52, 76.
2. Определите закономерность, по которой записаны числа а) верхней строки; б) каждого столбца, – и продолжите ряды чисел. 16 26 27 37 38 * * * * 6 25 17 36 28 * * * * IV. Изучение нового материала. 1. На доске: 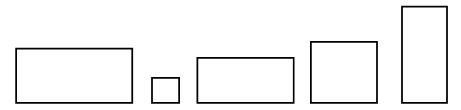 – Чем похожи изображенные фигуры? – Чем отличаются? – Распределите фигуры на две группы по их отличительным признакам. В ы п о л н е н и е з а д а н и я: 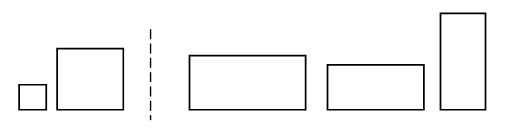 – Рассмотрите внимательно фигуры второй группы. – Что в них общего? У прямоугольника все углы прямые, а противоположные стороны равны. 2. Практическая работа. Учитель раздает учащимся вырезанные из бумаги в клетку прямоугольники, просит детей сложить прямоугольники пополам и проверить, действительно ли противоположные стороны равны. Необходимо перегибание модели произвести дважды: первый раз горизонтально, второй – вертикально.  3. Работа с учебником. Дети читают текст из задания 1 (с. 28 учебника, часть 2). – Догадались, что изменилось в фигуре? – Совершенно верно, углы. В новой фигуре они не прямые, и, следовательно, данную фигуру нельзя назвать прямоугольником. (Учитель может сообщить ученикам о том, что такая фигура называется параллелограмм.)  V. Работа над задачами. Учащиеся читают текст в задании 2 (с. 28 учебника, часть 2). – Что хотите сказать? – Почему считаете, что прочитанный вами текст не является задачей? – Поставьте такой вопрос, чтобы задача решалась сложением. (Сколько всего деталей понадобилось Никите?) – Измените вопрос так, чтобы задача решалась вычитанием. (На сколько больше деталей потребовалось Никите для изготовления подъёмного крана, чем для изготовления тележки? Или: На сколько меньше деталей потребовалось Никите для изготовления тележки, чем для изготовления подъёмного крана?) – Дайте ответы на поставленные вами вопросы. После этой работы учащиеся составляют задачи по выражениям: 36 + (36 – 8) 36 + (36 + 8) VI. Решение выражений. Учащиеся выполняют с комментированием задание 4 (с. 28 учебника, часть 2). Затем им может быть предложена самостоятельная работа по карточкам. Учащиеся записывают выражения столбиком и находят их значения. К-1. 32 – 15 24 + 47 50 – 36 13 + 67 К-2. 45 – 18 36 + 19 70 – 32 22 + 58 К-3. 91 – 78 35 + 27 60 – 46 28 + 32 VII. Итог урока. – Чему научил вас сегодняшний урок? – Какие открытия вы сделали? – Какую работу вам бы хотелось выполнить ещё? – Как вы сегодня работали? У р о к 88. РАБОТА НАД ЗАДАЧАМИ И ВЫРАЖЕНИЯМИ. ПРЯМОУГОЛЬНИК Цели: закреплять знания учащихся о том, что прямоугольник – это четырёхугольник, у которого все углы прямые и противоположные стороны равны; продолжать пропедевтику темы «Умножение»; развивать навыки счёта, умение решать простые и составные задачи, умение чертить геометрические фигуры. Ход урока I. Организационный момент. II. Каллиграфическая минутка. 25 25 25 25 25 37 37 37 37 37 III. Устный счёт. 1. Какое число пропущено? 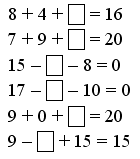 2. Вычислите удобным способом. 36 + 18 + 2 + 4 27 + 6 + 14 + 3 17 + 20 + 40 + 3 29 + 50 + 1 + 20 IV. Работа с геометрическим материалом. На доске изображены фигуры из задания на смекалку (на полях с. 29 учебника, часть 2). – Что хотите сказать? – Есть ли среди данных фигур хоть один прямоугольник? – Почему так считаете? – Начертите изображённые фигуры в своих тетрадях. – Дополните каждую из них до прямоугольника. – Как вы это сделали? – Как отличить прямоугольник от любого другого четырёхугольника? – Известно, что длины двух сторон прямоугольника равны 3 см и 6 см. Как узнать длины двух других сторон этого прямоугольника? – Начертите в тетрадях прямоугольник со сторонами 2 см и 5 см. – Проверьте работу друг друга. – Как найти периметр данного прямоугольника? – Найдите периметр изображённого вами прямоугольника. – Чему он равен?  V. Работа над задачами. Учащиеся читают текст задачи 3 (с. 29 учебника, часть 2). – Вы прочитали задачу? – Докажите. – Чем эта задача непохожа на те, которые мы с вами уже решали? – Кто из вас догадался, какой формы была комната? – Как бы вы предложили решить эту задачу? – Удобнее ли будет решать задачу при помощи чертежа? – Выполните чертёж. За 1 метр примите 1 сантиметр. – Найдите длину полоски. – Какова длина полоски? – Запишите ответ. Далее ученики рассматривают краткие записи задач в задании 4 (с. 29 учебника, часть 2), а затем составляют по ним задачи, которые позже решают самостоятельно с последующей взаимопроверкой. VI. Пропедевтика темы «Умножение». С этой целью устно выполняется задание 6 (с. 29 учебника, часть 2) и с комментированием задание 7 (с. 29 учебника, часть 2). VII. Самостоятельная работа. В качестве самостоятельной работы учащимся может быть предложено задание 8 (с. 29 учебника, часть 2), которое способствует закреплению учениками изученных приёмов сложения и вычитания двузначных чисел. VIII. Итог урока. – Чему научились сегодня на уроке? – Всё ли было понятно? – Какие задания вызвали наибольшие затруднения? – Как вы думаете, почему? – Чью бы работу вам хотелось отметить? У р о к 89. КВАДРАТ Цели: дать учащимся представление о квадрате как о четырёхугольнике, у которого все углы прямые и все стороны равны; развивать умение учеников находить периметр многоугольников, продолжать работу над задачами; развивать навыки счёта. Ход урока I. Организационный момент. II. Каллиграфическая минутка. 8 80 8 80 8 80 18 18 18 18 18 < > < > < > III. Устный счёт. 1. «Магические квадраты». 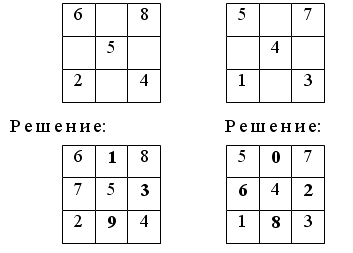 2. Ребусы. *8 – * = 20 *9 – * = 40 60 84 +2* –*6 *5 4* IV. Письменное сложение и вычитание двузначных чисел. На данном этапе урока ученикам может быть предложено задание 4 (с. 30 учебника, часть 2), а также аналогичные задания, подобранные учителем. Задание может быть выполнено как фронтально, так и индивидуально либо в парах (на усмотрение учителя или учащихся). V. Изучение нового материала. На доске изображены геометрические фигуры: 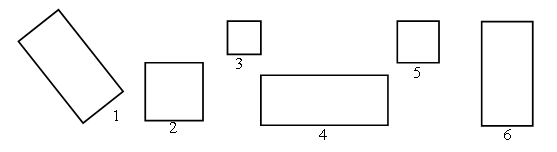 – Что хотите сказать? – Найдите на чертеже и назовите номера тех прямоугольников, у которых все стороны равны. – Прямоугольник, у которого все стороны равны, – квадрат. – Начертите в тетрадях квадрат, длина стороны которого равна 2 сантиметрам. – Найдите периметр этого квадрата. – Чему он равен? VI. Работа над задачами. На доске записаны выражения: 100 – (25 + 15) (20 + 20) + 50 – Рассмотрите внимательно выражения. – Составьте по ним задачи. Данную работу учащиеся могут выполнить по вариантам. – Решите составленные вами задачи. – Проверьте свою работу. (Самопроверка с доски или контрольного листа.) VII. Решение выражений и уравнений. На данном этапе урока ученики выполняют задания 5, 7 (с. 30 учебника, часть 2). Задание 5 может быть выполнено с комментированием либо в парах с последующей фронтальной проверкой. Работу над уравнениями можно провести следующим образом: ученики решают уравнения самостоятельно, в это время трое учащихся выполняют работу на закрытой доске (решая каждый по одному уравнению). Фронтальная проверка. VIII. Итог урока. – Чему научил вас урок? – Какие открытия сделали? – Какое задание вам понравилось больше других? – Чем? – Какую бы работу вам хотелось выполнить ещё? – Оцените свою работу. У р о к 90. РЕШЕНИЕ ЗАДАЧ И ВЫРАЖЕНИЙ Цели: закреплять знания учащихся о том, что квадрат – это прямоугольник, у которого все стороны равны; развивать умение учеников применять на практике изученные приёмы сложения и вычитания двузначных чисел; продолжать работу над задачами; развивать навыки счёта, мышление, внимание учеников. Ход урока I. Организационный момент. II. Каллиграфическая минутка. 0 0 0 0 0 0 10 10 10 10 10 100 100 100 100 – Что хотите сказать о записанных вами числах? – Одинакова ли роль нуля в них? – А роль единицы в числе 10 и числе 100? III. Устный счёт. 1. Найдите значения выражений: а + 8 и b – 6 при: а = 14 b = 13 а = 8 b = 18 а = 6 b = 44 а = 47 b = 50 2. Рассмотрите записанные суммы и, не вычисляя, определите, значение какой из них больше: 8 + 7+ 15 + 65 7 + 65 + 20 + 8 – Объясните, как вы рассуждали. IV. Работа над задачами. Учитель предлагает ученикам рассмотреть краткие записи в задании 3 (с. 31 учебника, часть 2). – Что заметили? – Будут ли данные задачи обратными? – Почему так считаете? – Какая из записанных задач составная? – Что можно сказать о первой задаче? – Составьте задачи. – Запишите их решение. – Проверьте свою работу. (Самопроверка.)  Далее учащиеся читают текст задачи 2 (с. 31 учебника, часть 2), выделяют условие и вопрос, называют данные и искомое числа, записывают задачу кратко или при помощи схемы и решают её. После того как задача решена, к ней составляются две обратные задачи. (В одной посылке 8 килограммов яблок. Сколько килограммов в другой посылке, если всего в двух посылках было 14 килограммов яблок? В одной посылке 6 килограммов яблок, а в другой – 8 килограммов. Сколько килограммов яблок в двух посылках?) Учащиеся решают задачи самостоятельно с последующей взаимопроверкой. V. Решение выражений. C подробным объяснением на доске и последующей проверкой выполняется задание 4 (с. 31 учебника, часть 2), в котором дети находят значения выражений в столбик. После этого ученики выполняют задание 5 (с. 31 учебника, часть 2). Часть задания может быть выполнена с комментированием, часть – самостоятельно с последующей фронтальной проверкой. VI. Работа с геометрическим материалом. – Рассмотрите фигуры, изображённые в задании 1 (с. 31 учебника, часть 2). – Что хотите сказать? – Какие из этих фигур – квадраты? – Обоснуйте ваше мнение. – Чем похожи и чем отличаются фигуры 1 и 2, 2 и 3, 3 и 4? После этой работы учитель читает ученикам задачу на смекалку – задание 2 (с. 32 учебника, часть 2). Р е ш е н и е: Белочка начертила треугольник. Учитель может несколько изменить задание, спросив учащихся о том, какую фигуру начертил каждый ученик лесной школы. Р е ш е н и е: Ёж – круг. Заяц – прямоугольник. Лиса – квадрат. Белочка – треугольник. VII. Итог урока. – Чему научил вас урок? – Что особенно запомнилось? – Какую работу вам бы хотелось выполнить ещё? – Как вы сегодня работали? У р о к 91. ЗАКРЕПЛЕНИЕ ЗНАНИЙ УЧАЩИХСЯ Цели: закреплять умения учащихся использовать изученные приёмы письменного сложения и вычитания, решать уравнения; продолжать работу над задачами; развивать мышление, навыки устного счёта. Ход урока I. Организационный момент. II. Каллиграфическая минутка. 17 17 17 17 17 21 21 21 21 21 III. Устный счёт. 1. Ребусы. *5 18 34 ** –1* +1* +2* –15 57 *2 *0 64 2. Задание 14 (с. 34 учебника, часть 2). Используя таблицу (ее лучше начертить на доске), учащиеся составляют выражения и находят их значения. Выполняя предложенное задание, ученики повторяют термины «слагаемое», «сумма». IV. Решение выражений. Учащиеся выполняют задание 1 (с. 33 учебника, часть 2) следующим образом: • выражения под первой скобкой решаются устно с подробным объяснением; • часть выражений, данных под второй и третьей скобками, решается на доске с подробным объяснением, остальные выражения (под скобками два и три) ученики решают самостоятельно с последующей фронтальной проверкой; • после этого с комментированием выполняется задание 6 (с. 33 учебника, часть 2). Выполняя это задание, дети повторяют порядок действий в выражениях со скобками. V. Работа над задачами. Учащиеся читают задачу 11 (с. 34 учебника, часть 2). – Что заметили? – Дополните задачу. – Запишите её кратко и решите. (Двое учащихся выполняют работу на закрытой доске.) – Посмотрите, так ли вы записали и решили задачу. – Можно ли было это сделать по-другому?  Фронтально разбирается задача 12 (с. 34 учебника, часть 2). Ученики выделяют условие и вопрос, называют данные и искомые числа. Далее составляется краткая запись, после чего учитель сообщает учащимся о том, что такую задачу можно записать кратко иначе: используя таблицу.
Решение задачи учащиеся выполняют самостоятельно с последующей фронтальной проверкой. В парах разбирается и решается задача 10 (с. 34 учебника, часть 2). |
