Алушкина Начертательная геометрия. Самостоятельная работа по изучению дисциплины 6 2 Методика выполнения контрольных работ 8 2 Содержание дисциплины Начертательная геометрия

• Название: Самостоятельная работа по изучению дисциплины 6 2 Методика выполнения контрольных работ 8 2 Содержание дисциплины Начертательная геометрия
• Дата: 18.01.2022
• Размер: 1.72 Mb.
• Имя файла: Алушкина Начертательная геометрия.doc
• Тип: Самостоятельная работа; #334581
• страница: 2 из 8

5 КОНТРОЛЬНАЯ РАБОТА № 1

(листы 1, 2, 3)

5.1 Лист 1

Задача 1. Построить линию пересечения треугольников АВС и EDKи показать их видимость в проекциях. Определить натуральную величину треугольника АВС. Данные для своего варианта взять из таблицы 2. Пример выполнения листа 1 дан на рисунке 2.

Указания к решению задачи 1. В левой половине листа формата А3 (297^х420) намечаются оси координат и из таблицы 1 согласно своему варианту берутся координаты точек А, В, С, D, Е. К вершин треугольника (рисунок А2). Стороны треугольников и другие вспомогательные прямые проводятся вначале тонкими сплошными линиями. Линия пересечения треугольников строится по точкам пересечения сторон одного треугольника со стороной другого треугольника или по точкам пересечения каждой из сторон одного треугольника с другим порознь. Такую линию можно построить, используя и вспомогательные секущие проецирующие плоскости.

Видимость сторон треугольников определяется способом конкурирующих точек. Видимые отрезки сторон треугольников выделяют сплошными жирными линиями, невидимые следует показать штриховыми или тонкими линиями. Определяется натуральная величина треугольника АВС.

Плоскопараллельным перемещением треугольник АВС приводится в положение проецирующей плоскости, и далее вращением вокруг проецирующей прямой треугольник ABCприводится в положение А₁В₁С₁,когда он будет параллелен плоскости проекций. В треугольнике ABCследует показать и линию пересечения его с треугольником EDK.

Выполнив все построения в карандаше, чертеж обводят тушью или цветной пастой шариковой ручки. Вначале, используя балеринку (трафарет), помечают кружками характерные точки. Черной тушью (пастой) обводят линии заданных треугольников, красной тушью (пастой) обводят линию пересечения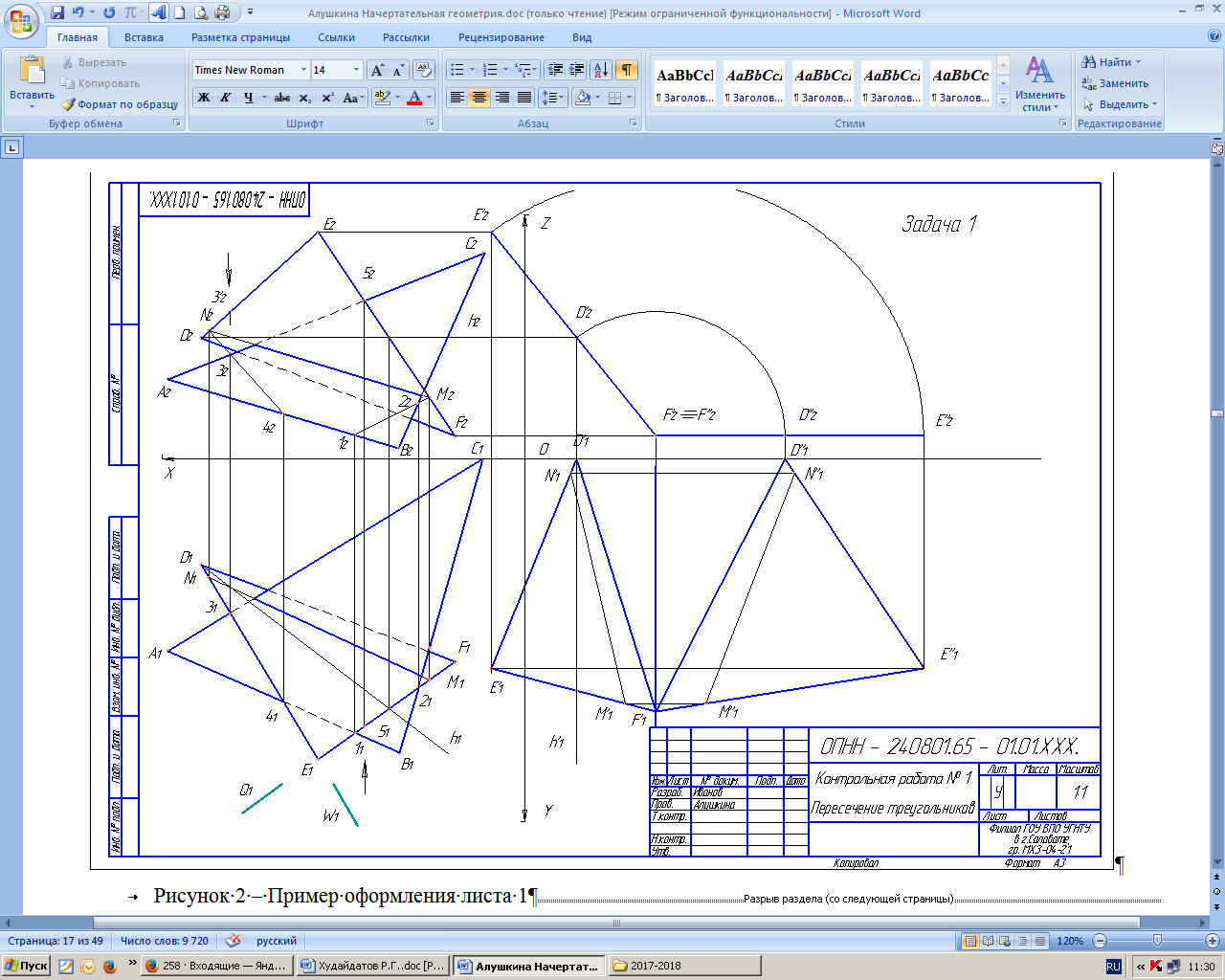



Рисунок 2 – Пример оформления листа 1

треугольников. Все вспомогательные построения должны быть обязательно показаны на чертеже в виде тонких линий синей (зеленой) тушью (пастой).

Видимые части треугольников в проекциях можно покрыть очень бледными тонами красок или цветных карандашей. Все буквенные или цифровые обозначения, а также надписи обводятся черной тушью (пастой).

Таблица 2 - Данные к задаче 1 (размеры и координаты, мм)

№ варианта	Точка А			Точка В			Точка С			Точка D			Точка Е			Точка К
	x	y	z	x	y	z	x	y	z	x	y	z	x	y	z	x	y	z
1	117	90	9	52	25	79	0	83	48	68	110	85	135	19	36	14	52	0
2	120	90	10	50	25	80	0	85	50	70	110	85	135	20	35	15	50	0
3	115	90	10	52	25	80	0	80	45	65	105	80	130	18	35	12	50	0
4	120	92	10	50	20	75	0	80	46	70	115	85	135	20	32	10	50	0
5	117	9	90	52	79	25	0	48	83	68	85	110	135	36	19	14	0	52
6	115	7	85	50	80	25	0	50	85	70	85	110	135	40	20	15	0	50
7	120	10	90	48	82	20	0	52	82	65	80	110	130	38	20	15	0	52
8	116	8	88	50	78	25	0	46	80	70	85	108	135	36	20	15	0	52
9	115	10	92	50	80	25	0	50	85	70	85	110	135	35	20	15	0	50
10	18	10	90	83	79	25	135	48	83	67	85	110	0	36	19	121	0	52
11	20	12	92	85	80	25	135	50	85	70	85	110	0	35	20	120	0	52
12	15	10	85	80	80	20	130	50	80	70	80	108	0	35	20	120	0	50
13	16	12	88	85	80	25	130	50	80	75	85	110	0	30	15	120	0	50
14	18	12	85	85	80	25	135	50	80	70	85	110	0	35	20	120	0	50
15	18	90	10	83	25	79	135	83	48	67	110	85	0	19	36	121	52	0
16	18	40	75	83	117	6	135	47	38	67	20	0	0	111	48	121	78	86
17	18	75	40	83	6	107	135	38	47	67	0	20	0	48	111	121	86	78
18	117	75	40	52	6	107	0	38	47	135	0	20	68	48	111	15	86	78
19	117	40	75	52	107	6	0	47	38	135	20	0	68	111	48	15	78	86
20	120	38	75	50	108	5	0	45	40	135	20	0	70	110	50	15	80	85
21	122	40	75	50	110	8	0	50	40	140	20	0	70	110	50	20	80	85
22	20	40	10	85	110	80	135	48	48	70	20	85	0	110	35	120	80	0

Продолжение таблицы 2

№ варианта	Точка А			Точка В			Точка С			Точка D			Точка Е			Точка К
	x	y	z	x	y	z	x	y	z	x	y	z	x	y	z	x	y	z
23	20	10	40	85	80	110	135	48	48	70	85	20	0	35	110	120	0	80
24	117	40	9	52	111	79	0	47	48	68	20	85	135	111	36	14	78	0
25	117	9	40	52	79	111	0	48	47	68	85	20	135	36	111	14	0	78
26	18	40	9	83	111	79	135	47	48	67	20	85	0	111	36	121	78	0
27	18	9	40	83	79	111	135	48	47	67	85	20	0	36	111	121	0	78

5.2 Лист 2

Задача 2. Построить проекции пирамиды, основанием которой является треугольник ABC, аребро SAопределяет высоту hпирамиды. Данные для своего варианта взять из таблицы 3.

Задача 3. Построите линию пересечения пирамиды с прямой призмой. Данные для своего варианта взять из таблицы 4. Пример выполнения листа 2 дан на рисунке 3.

Указания к решению задачи 2. В левой половине листа формата А3 намечаются оси координат и из таблицы 3 согласно своему варианту берутся координаты точек А, В и С вершин треугольника ABC. По координатам строится треугольник в проекциях. В точке А восставляется перпендикуляр к плоскости треугольника и на нем выше этой плоскости откладывается отрезок AS, равный заданной величине h. Строятся ребра пирамиды. Способом конкурирующих точек определяется их видимость. Видимые ребра пирамиды следует показать сплошными жирными линиями, невидимые — штриховыми линиями. Стороны треугольника ABC(основание пирамиды) следует показать черной тушью (пастой); ребра SA, SB,и SС пирамиды показать красной тушью (пастой). Все вспомогательные построения необходимо сохранить на эпюре и показать их тонкими сплошными линиями зеленой (синей) тушью или пастой шариковой ручки.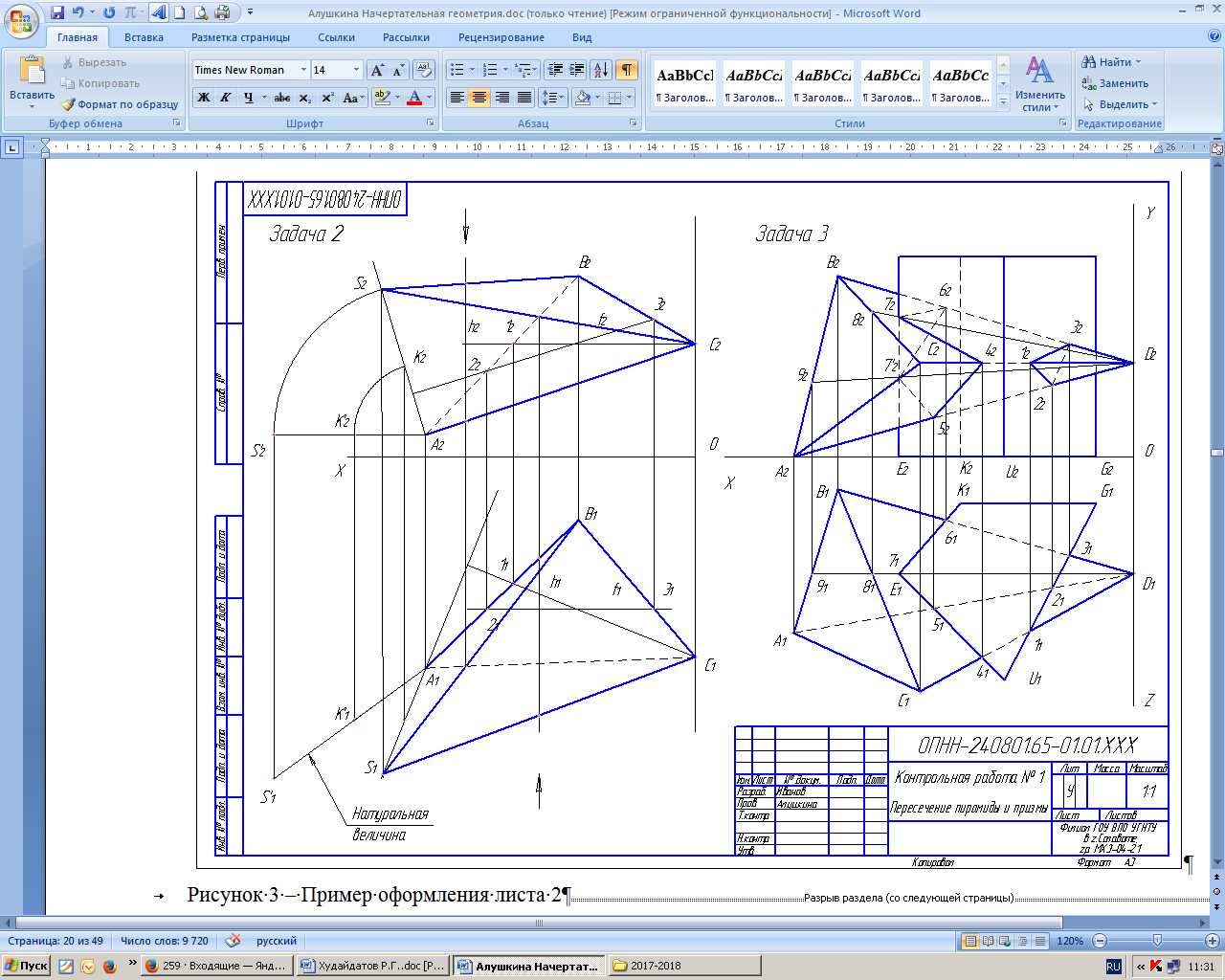


Рисунок 3 – Пример оформления листа 2

Указания к решению задачи 3. В оставшейся правой половине листа намечаются оси координат и из таблицы 4 согласно своему варианту берутся координаты точек А, В, С и Dвершин пирамиды и координаты точек Е, К, G и Uвершин многоугольника нижнего основания призмы, атакже высота hпризмы. По этим данным строятся проекции многогранников (пирамида и призма). Призма своим основанием стоит на плоскости уровня, горизонтальные проекции ее вертикальных рёбер преобразуются в точки. Грани боковой поверхности призмы представляют собой отсеки горизонтально-проецирующих плоскостей.

Линия пересечения многогранников определяется по точкам пересечения ребер каждого из них с гранями другого многогранника или построением линией пересечения граней многогранников. Соединяя каждые пары таких точек одних и тех же граней отрезками прямых, получаем линию пересечения многогранников.