Алушкина Начертательная геометрия. Самостоятельная работа по изучению дисциплины 6 2 Методика выполнения контрольных работ 8 2 Содержание дисциплины Начертательная геометрия

• Название: Самостоятельная работа по изучению дисциплины 6 2 Методика выполнения контрольных работ 8 2 Содержание дисциплины Начертательная геометрия
• Дата: 18.01.2022
• Размер: 1.72 Mb.
• Имя файла: Алушкина Начертательная геометрия.doc
• Тип: Самостоятельная работа; #334581
• страница: 3 из 8

Таблица 3 - Данные к задаче 2 (координаты и размеры, мм)

№ ва-рианта	хА	уА	zА	xВ	уВ	zВ	xС	уС	zС	n
1	117	90	9	52	25	79	0	83	48	85
2	120	90	10	50	25	80	0	85	50	85
3	115	90	10	52	25	80	0	80	45	85
4	120	92	10	50	20	75	0	80	46	85
5	117	9	90	52	79	25	0	48	83	85
6	115	7	85	50	80	25	0	50	85	85
7	120	10	90	48	82	20	0	52	82	85
8	116	8	88	50	78	25	0	46	80	85
9	115	10	92	50	80	25	0	50	85	85
10	18	10	90	83	79	25	135	48	83	85
11	20	12	92	85	80	25	135	50	85	85
12	15	10	85	80	80	20	130	50	80	85
13	16	12	88	85	80	25	130	50	80	80
14	18	12	85	85	80	25	135	50	80	80
15	18	90	10	83	25	79	135	83	48	80

Продолжение таблицы 3

№ ва-рианта	хА	уА	zА	xВ	уВ	zВ	xС	уС	zС	n
16	18	40	75	83	117	6	135	47	38	80
17	18	75	40	83	6	107	135	38	47	80
18	117	75	40	52	6	107	0	38	47	80
19	117	40	75	52	107	6	0	47	38	80
20	120	38	75	50	108	5	0	45	40	80
21	122	40	75	50	110	8	0	50	40	85
22	20	40	10	85	110	80	135	48	48	80
23	20	10	40	85	80	110	135	48	48	85
24	117	40	9	52	111	79	0	47	48	80
25	117	9	40	52	79	111	0	48	47	85
26	18	40	9	83	111	79	135	47	48	80
27	18	9	40	83	79	111	135	48	47	80

Видимыми являются только те стороны многоугольника пересечения, которые принадлежат видимым граням многогранников. Их следует показать сплошными жирными линиями красной тушью (пастой). Невидимые отрезки пространственной ломаной показать штриховыми линиями красной тушью (пастой). Все вспомогательные построения на эпюре сохранить и показать их тонкими линиями синей (зеленой) тушью или пастой шариковой ручки.

П р и м е ч а н и е. Задаче 3 уделить особое внимание. Все построения на чертеже тщательно проверить. Допущенные здесь ошибки приводят к неправильному решению следующей задачи — задачи 4 (построение разверток многогранников)

Таблица 4 - Данные к задаче 3 (координаты и размеры, мм)

№ ваварианта ваввваавввввваввввввввввввввввввввввариа ваарианта	xА	уа	Zа	xв	уВ	zВ	xС	уС	zС	xD	yD	zD	xE	yE	zE	xK	yK	zK	xG	yG	zG	xU	yU	zU	h
1	141	75	0	122	14	77	87	100	40	0	50	40	100	50	0	74	20	0	16	20	0	55	95	0	85
2	0	70	0	20	9	77	53	95	40	141	45	40	40	50	0	67	20	0	125	20	0	86	95	0	85
3	0	80	0	20	19	77	53	110	40	141	55	40	40	50	0	67	20	0	125	20	0	86	95	0	85
4	0	68	0	20	7	77	53	93	40	141	43	40	40	50	0	67	20	0	125	20	0	86	95	0	85
5	0	75	0	20	14	77	53	100	40	141	50	40	40	50	0	67	20	0	125	20	0	86	95	0	85
6	0	82	0	20	21	77	53	112	40	141	57	40	40	50	0	67	20	0	125	20	0	86	95	0	85
7	0	85	0	20	24	77	53	115	40	141	60	40	40	50	0	67	20	0	125	20	0	86	95	0	85
8	0	90	0	20	29	77	53	120	40	141	65	40	40	50	0	67	20	0	125	20	0	86	95	0	85
9	0	85	0	15	30	80	55	120	40	141	60	40	40	50	0	67	20	0	125	20	0	86	95	0	85
10	141	70	0	122	9	77	87	95	40	0	45	40	100	50	0	74	20	0	16	20	0	55	95	0	85
11	141	80	0	122	19	77	87	110	40	0	55	40	100	50	0	74	20	0	16	20	0	55	90	0	85
12	141	68	0	122	7	77	87	93	40	0	43	40	100	50	0	74	20	0	16	20	0	55	95	0	85
13	141	82	0	122	21	77	87	112	40	0	57	40	100	50	0	74	20	0	16	20	0	55	95	0	85
14	141	85	0	122	24	77	87	115	40	0	60	40	130	50	0	74	20	0	16	20	0	55	95	0	85
15	141	90	0	122	29	77	87	120	40	0	65	40	100	50	0	74	20	0	16	20	0	55	95	0	85
16	135	75	0	116	14	77	81	100	40	0	50	40	100	50	0	74	20	0	16	20	0	55	95	0	85
17	145	75	0	126	14	77	91	100	40	0	50	40	100	50	0	74	20	0	16	20	0	55	95	0	85
18	145	95	0	120	34	77	87	120	60	0	70	60	100	50	0	74	20	0	16	20	0	55	95	0	85
19	145	70	0	122	10	80	90	95	45	0	70	45	100	50	0	74	20	0	16	20	0	55	95	0	85
20	145	65	0	122	20	70	85	100	47	0	68	47	100	50	0	74	20	0	16	20	0	55	95	0	85
21	122	14	77	141	75	0	87	100	40	0	50	40	105	55	0	80	15	0	20	20	0	50	95	0	85
22	120	15	80	140	75	0	85	100	45	0	50	45	105	55	0	80	15	0	20	20	0	50	95	0	85
23	125	20	80	140	75	0	85	100	45	0	55	45	98	52	0	76	20	0	18	22	0	57	95	0	85
24	140	70	0	120	15	80	85	95	45	0	50	45	100	50	0	75	22	0	20	20	0	60	90	0	85
25	140	65	0	115	20	75	80	90	40	0	50	40	100	45	0	75	17	0	22	25	0	60	95	0	85
26	135	65	0	120	20	75	80	90	45	0	55	45	100	48	0	70	15	0	20	27	0	65	95	0	85
27	135	60	0	115	20	80	85	90	40	0	50	40	100	43	0	70	20	0	20	20	0	60	90	0	85

5.3 Лист 3

Задача 4. Построить развертки пересекающихся многогранников — прямой призмы с пирамидой. Показать на развертках линию их пересечения. Пример выполнения листа 3 дан на рисунке 4.

Чтобы решить данную задачу, чертеж-задание для листа 3 получить, переведя на кальку или миллиметровую бумагу формата 297^х420 чертеж пересекающийся многогранников с листа 2 (задача 3). Пример показан на рисунке 5.

Указания к решению задачи 4. Заданные элементы многогранников на кальке показать черным цветом туши (пасты); линию их пересечения обвести красным цветом туши (пасты). Здесь выполняются вспомогательные построения (их обвести синей или зеленой тушью или пастой шариковой ручки) для определения натуральных величин ребер многогранников.

На листе бумаги ватман формата А3 (297^Х420) строятся развертки многогранников.

Р а з в е р т к а п р я м о й п р и з м ы. Для построения развертки прямой призмы поступают следующим образом:

а) проводят горизонтальную прямую;

б) от произвольной точки этой прямой Gна прямой откладывают отрезки GU, UE, ЕК, KG, равные длинам сторон основания призмы;

в) из точек G, U... восставляют -перпендику­ляры и на них откладывают величины, равные высоте призмы. Полученные точки соединяют прямой. Прямоугольник GG₁G₁ Gявляется разверткой боковой поверхности призмы. Для указания на развертке граней призмы из точек U, Е, К восставляют перпендикуляры;

г) для получения полной развертки поверхности призмы к развертке поверхности пристраивают многоугольники ее оснований.

Для построения на развертке линии пересечения призмы с пирамидой — замкнутых ломаных линий 1 2 3 и 4 5 6 7 8 — пользуемся вертикальными прямыми. Например, для определения положения точки 1 на развертке посту-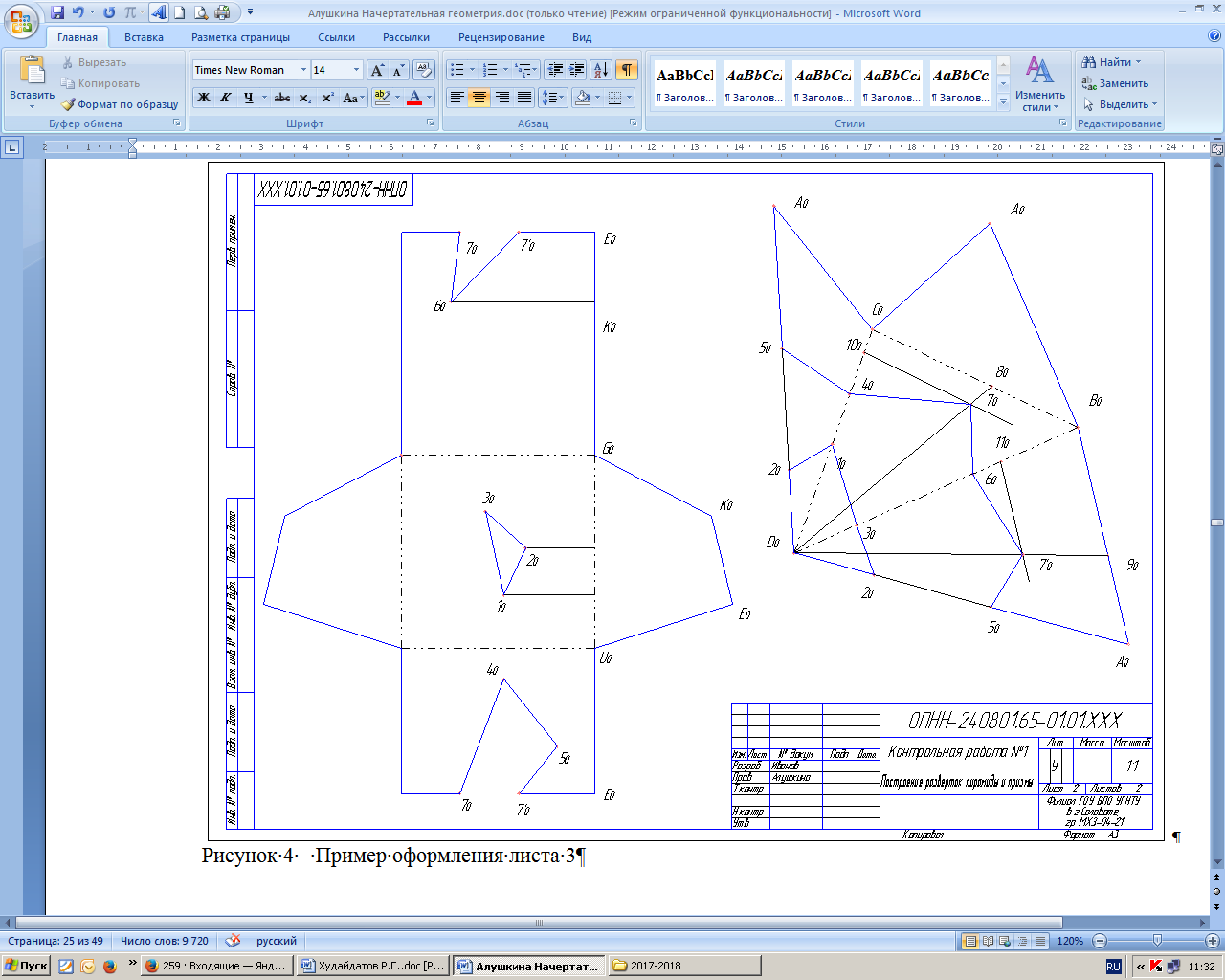



Рисунок 4 – Пример оформления листа 3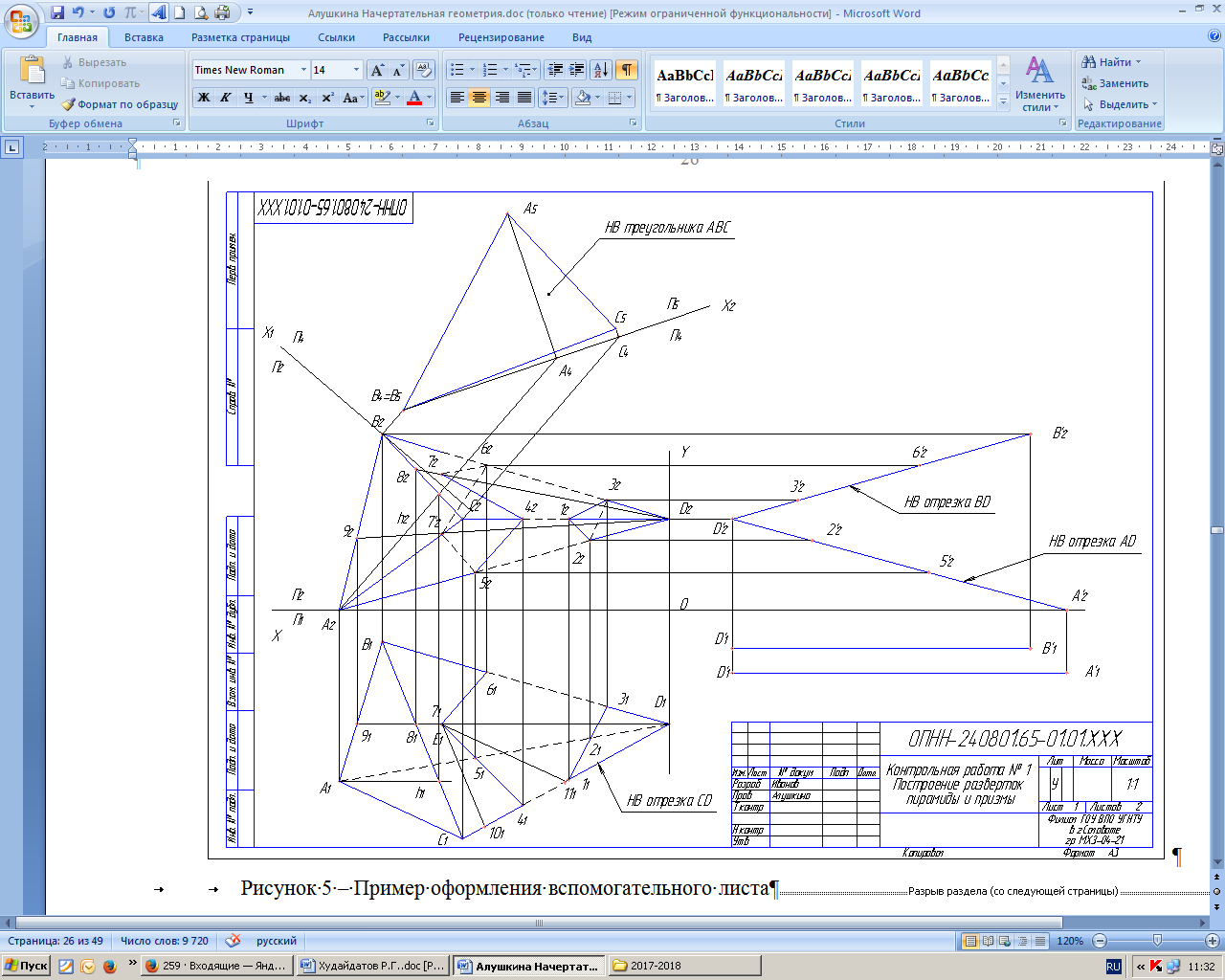



Рисунок 5 – Пример оформления вспомогательного листа

паем так: на отрезке GUот точки Gвправо откладываем отрезок G1_о, равный отрезку gl(рисунок 4).

Из точки 1о восставляем перпендикуляр к отрезку GUи на нем откладываем аппликату zточки1. Аналогично строят и находят и остальные точки.

Р а з в е р т к а п и р а м и д ы. На кальке определяют натуральную величину каждого из ребер пирамиды. Зная натуральные величины ребер пирамиды, строят ее развертку. Определяют последовательно натуральные величины граней пирамиды. На ребрах и на гранях пирамиды (на развертке) определяют вершины пространственной ломаной пересечения пирамиды с призмой.

Развертки многогранников покрыть бледным тоном цветной акварели, чая или цветного карандаша. Ребра многогранников на развертке обвести черной тушью (пастой); линии пересечения многогранников обвести красной, а все вспомогательные построения - синей /зеленой) тушью или пастой шариковой ручки.

Кальку и листы писчей бумаги с планом решения задачи наклеить с левого края листа 3.

Примечание: При построении разверток любых геометрических тел следует помнить, что откладывать на чертеже развертки можно только натуральные величины отрезков.