ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА. СанктПетербургский государственный электротехнический университет Н. П. Серебрянникова б. Е. Соботковский в. В. Морозов
 Скачать 1.09 Mb.
|
2.4. Нормальное или гауссово распределениеОдним из часто встречающихся на практике распределений является нормальный или гауссовский закон. Ему подчиняются физические величины, случайность которых обусловлена действием множества независимых (или слабо зависимых) малых аддитивных факторов, результат воздействия каждого из которых мал по сравнению с их суммарным воздействием. Плотность распределения вероятности нормального закона имеет вид 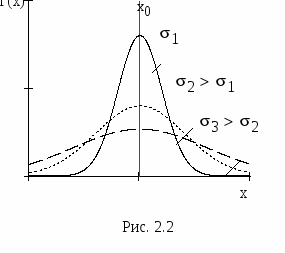 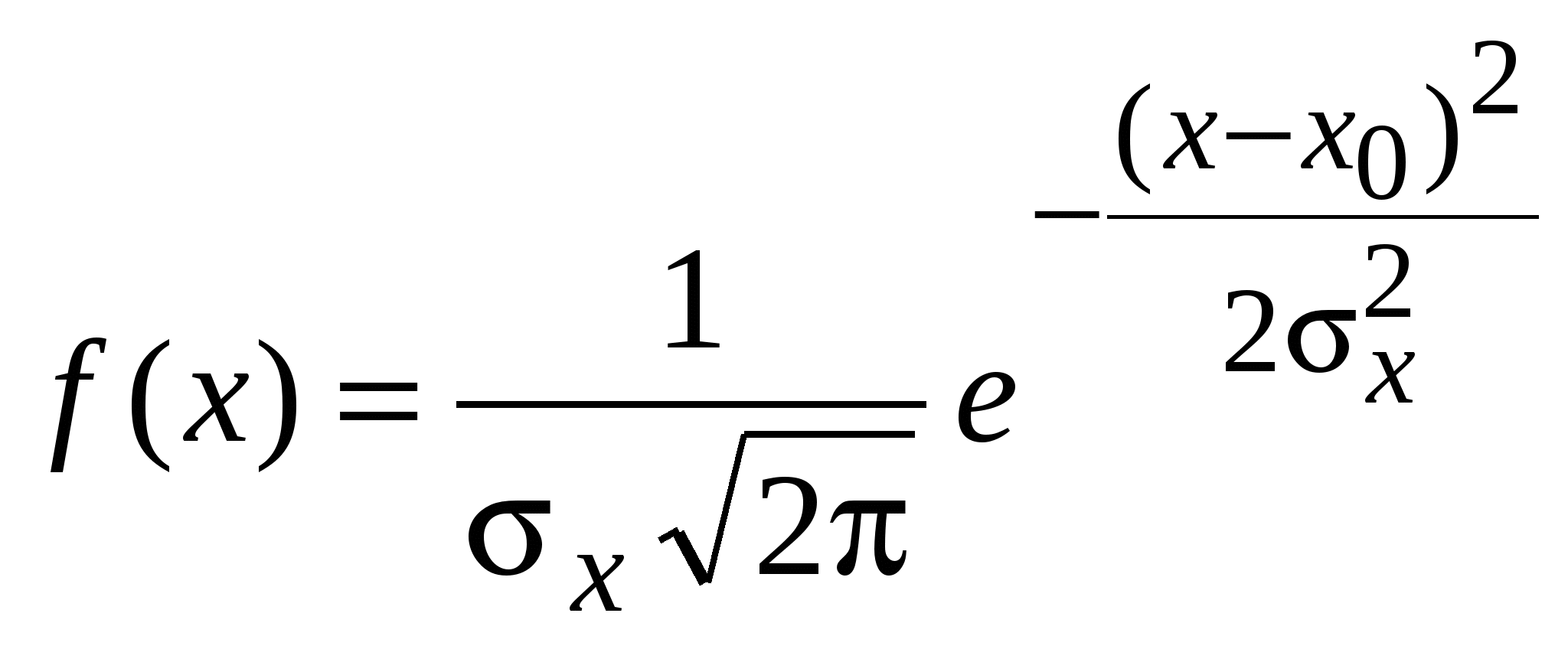 (2.4.1)где x – случайное значение величины X. Параметр x0 определяет центр распределения, а x форму и ширину кривой плотности распределения, что показано на рис. 2.2. В этом можно также убедиться, подставив (2.4.1) в (2.3.4), (2.3.5). Тогда получим, что  , а  или  . Множитель  перед экспонентой, определяющий высоту гауссовской кривой, выбран таким образом, чтобы было выполнено условие нормировки (2.3.3). Вероятность того, что случайное значение xвеличины X, распределенной по нормальному закону, попадет в заданный интервал (x1, x2) равна площади под графиком функции плотности вероятности f(x) в этом интервале. 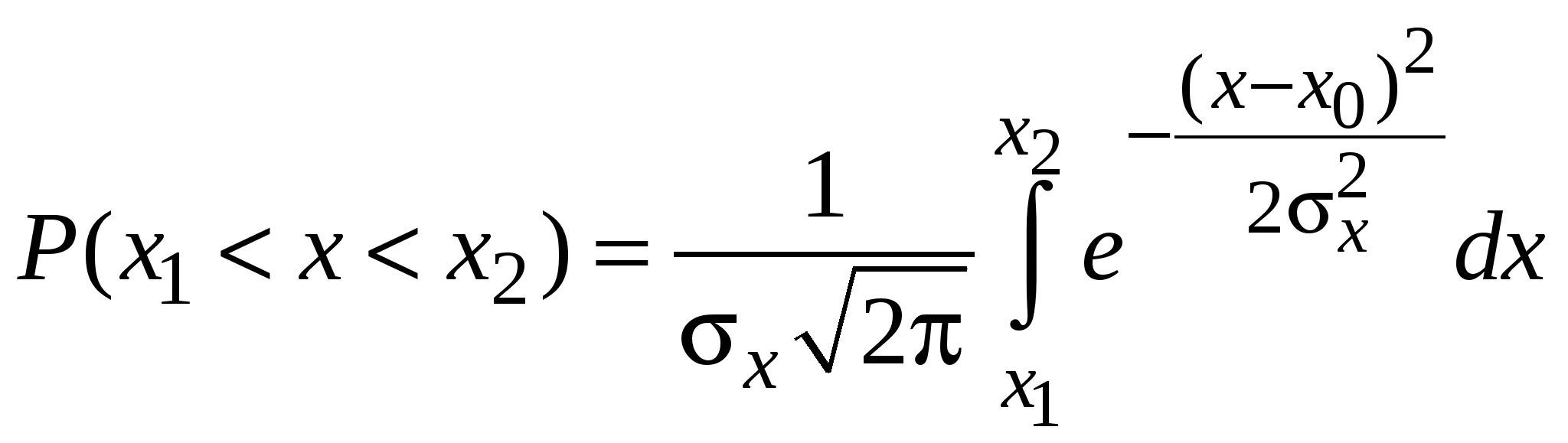 (2.4.2)Если интервал симметричный относительноx0, то его границы можно записать в виде  ,  , где tP – коэффициенты, определяющие ширину интервала в единицах x.Вводя новую переменную  , (2.4.2) можно записать в виде . (2.4.3)Вероятность P попадания u в интервал (–tP, tP) для разных значений tP можно найти, вычислив интеграл (2.4.3) численно. Соответствие между значениями P и tP для некоторых значений вероятности P дается таблицей:
Если значения коэффициентов tP найдены, то от переменной u можно вернуться к переменной x. Тогда из неравенства  получим  с вероятностью P или  с вероятностью P. 2.5. Результат измерения. Доверительный интервал.Задачей эксперимента является оценка истинного значения физической величины, которое может быть получено, только если мы располагаем генеральной совокупностью всех значений искомой величины Х. Однако, в связи с тем, что количество наблюдений в выборке конечно, в опыте находят некоторое приближенное к x0 значение  , которое называют оценкой истинного значения, и указывают интервал, в который истинное значение x0 попадает с заданной вероятностью P. Этот интервал называют доверительным, а вероятность Р – доверительной вероятностью. В качестве оценки истинного значения выбирают среднее арифметическое результатов наблюдений в выборке  , (2.5.1)которое называют также выборочным средним. Среднее также является случайной величиной, и если повторить опыт по его нахождению несколько раз, то получим выборку средних X:  ,  ...  , которые также будут отличаться друг от друга случайным образом, однако разброс средних значений будет заметно меньше разброса результатов отдельных наблюдений в каждой выборке.Для нахождения доверительного интервала необходимо знать распределение средних значений  около x0. З ная вид , можно построить интервал, в который истинное значение x0 попадает с вероятностью Р. Для этого на оси абсцисс (рис. 2.5.1) находят точки x1 иx2 такие, чтобы площади под графиком слева от x1 и справа x2 равнялись бы одной и той же величине  . Тогда площадь под графиком в интервале (x1, x2) будет равна значению вероятности P, и для произвольного полученного в опыте среднего значения можно написать: x1 < < x2 c вероятностью Р. Границы интервала можно записать в виде:  ,  . Если распределение симметрично, то  . Величину  в этом случае называют случайной доверительной погрешностью результата измерения. Можно показать, что если значения xвеличины X распределены по нормальному закону, то и рассчитываемые по ним средние значения также распределены по нормальному закону с центром в точке x0 и шириной распределения  , где N – объем выборок, по которым рассчитываются . Распределение средних будет описываться формулой (2.5.1), в которой x заменено на , а  на  . Если средние значения распределены по нормальному закону, то задача нахождения доверительного интервала сводится к нахождению доверительного интервала (– tP, tP) для стандартизованной переменной  и переходу к доверительному интервалу переменной . Решение этой задачи рассмотрено в предыдущем разделе. В результате получим, что границы интервала, в который случайное значение попадает с вероятностью P, определяется неравенством  с вероятностью P.Откуда для границ доверительного интервала x0 получаем  с вероятностью P,где tp – коэффициенты, соответствующие заданной вероятности Р. Это неравенство принято записывать в виде символического равенства  с вероятностью P, (2.5.2)где  – случайная доверительная погрешность результата измерения. |