ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА. СанктПетербургский государственный электротехнический университет Н. П. Серебрянникова б. Е. Соботковский в. В. Морозов

• Название: СанктПетербургский государственный электротехнический университет Н. П. Серебрянникова б. Е. Соботковский в. В. Морозов
• Анкор: ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА.doc
• Дата: 02.12.2017
• Размер: 1.09 Mb.
• Имя файла: ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА.doc
• Тип: Документы; #10600
• Категория: Физика
• страница: 7 из 14

2.7. Дисперсия суммы случайных величин. Дисперсия и среднеквадратичное отклонение среднего

Пусть Z = X + У есть сумма случайных величин X и У. Тогда среднее значение Z равно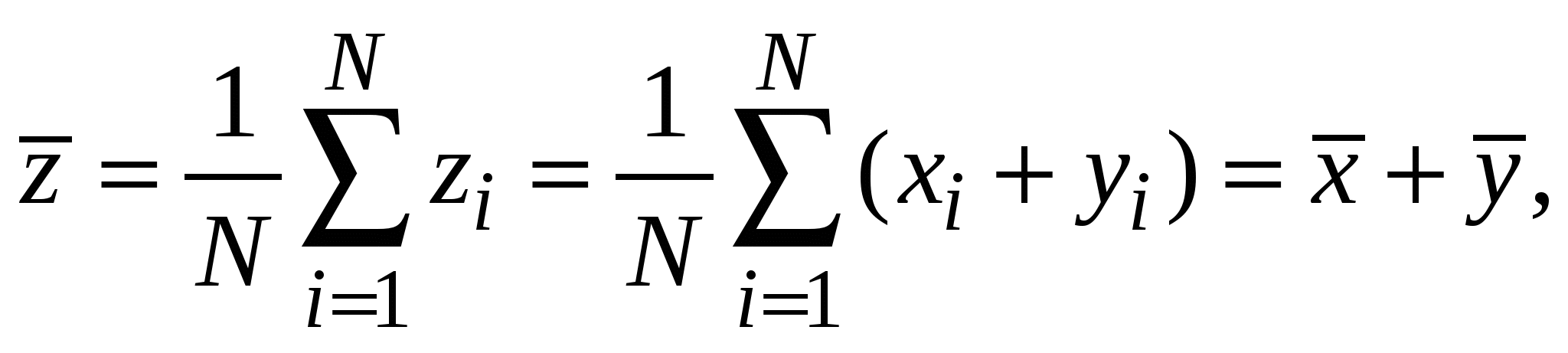



а дисперсия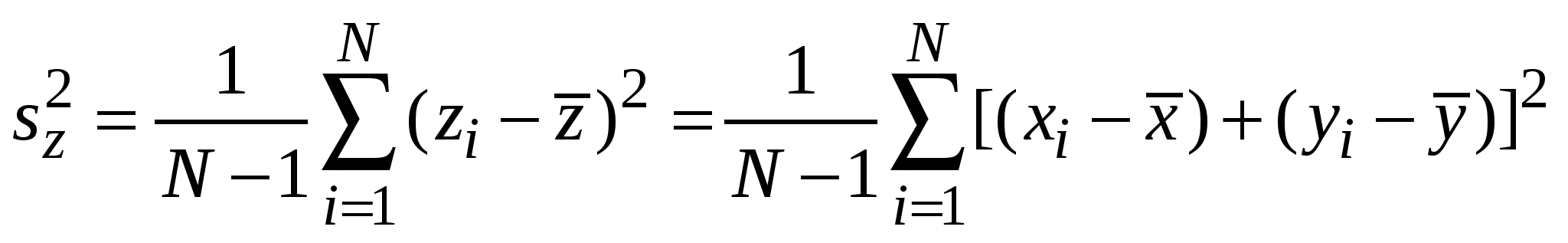



может быть представлена в виде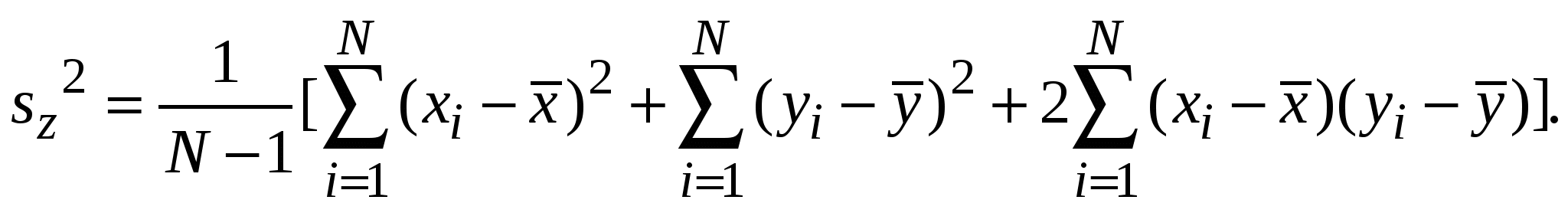



Если X и Y слу­чайны и независимы, то последняя сумма равна нулю, и

S_z² = S_x² + S_y².

т.е. дисперсии независимых случайных величин складываются линейно, а выборочные среднеквадратические отклонения – складываются квадратично.

Если Z = аХ + bY, то, повторив рассуждения, получим

S_z² = aS_x² + bS_y².

В случае суммы более двух случайных величин Z = a₁X₁+a₂X₂ +…+a_NX_N = ,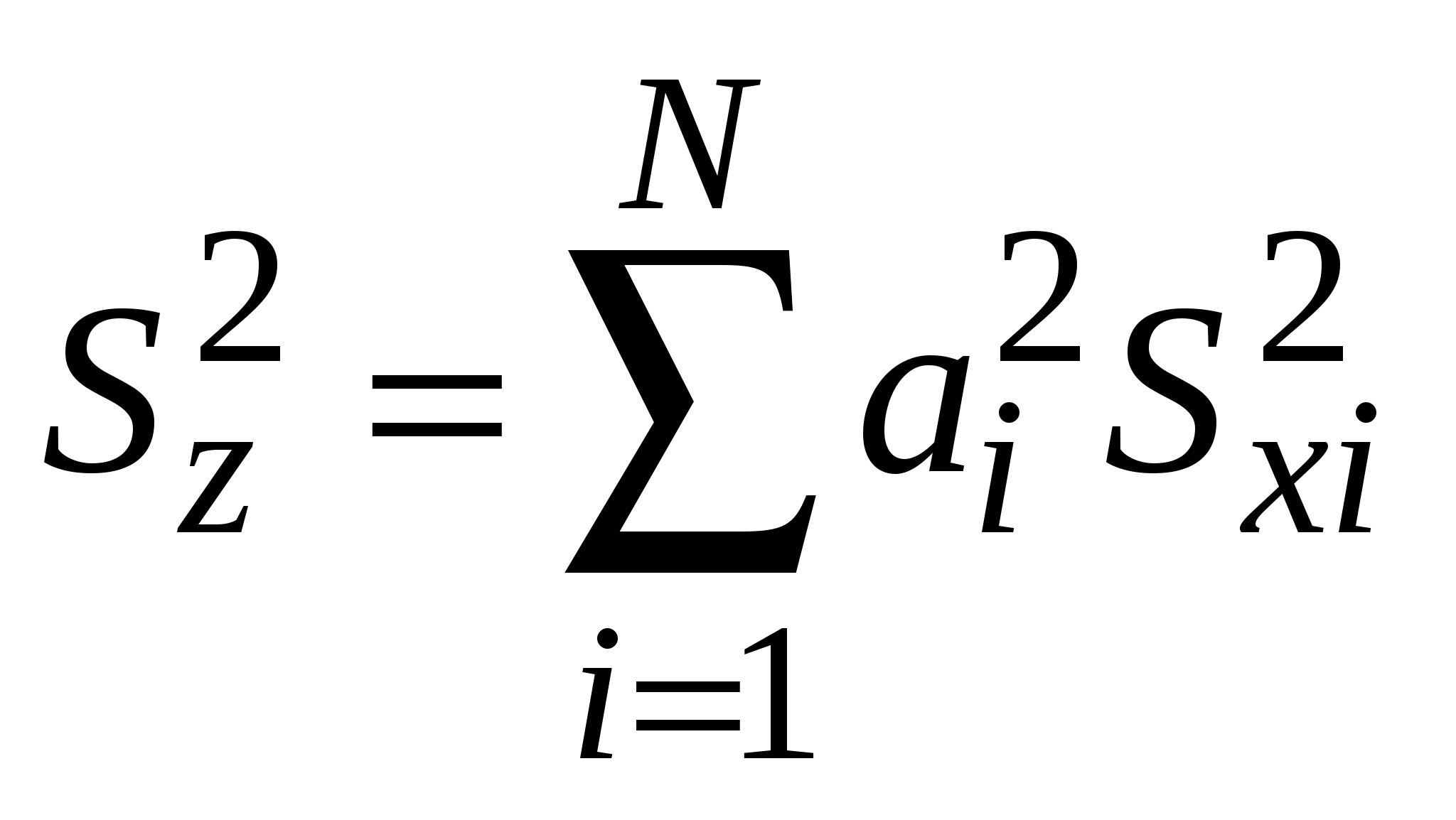

(2.7.1)

Для нахождения погрешности результата измерения представляет интерес не СКО результата отдельного наблюдения , а СКО сред­него значения .

Параметры и взаимосвязаны между собой. Эту, связь можно найти, если учесть, что среднее значение есть сумма N незави­симых случайных величин, дисперсии которых одинаковы

.

Тогда, ис­пользуя формулу (2.7.1), в которой а_i = 1/N, с учетом получим для дисперсии параметра :



Отсюда следует, что СКО

. (2.7.2)

2.8. Выявление грубых погрешностей

Среди результатов наблюдений в выборке значений измеряемой личины могут оказаться такие, которые сильно отличаются от ос­тальных: это либо промахи, либо результаты, содержащие грубые по­грешности.

Промахи (описки и т.п.) устраняют из таблицы наблюдений, не прибегая к каким-либо процедурам проверки, исходя лишь из здраво­го смысла. Для выявления результатов, содержащих грубые погрешно­сти, существуют различные статистические метода (критерии), в ос­нове которых, как правило, лежит предположение о том, что резуль­таты наблюдений принадлежат генеральной совокупности, элементы которой распределены по нормальному закону.

1.Рассмотрим сначала критерий, позволяющий по относительному расстоянию между крайним и ближайшим к нему предэкстремальным элементом упорядоченной выборки (x₁=x_minx₂… x_N = x_max) заключить, содержит ли крайний элемент выборки гру­бую погрешность или нет. Критерий основывается на анализе отношения , где величина R = x_max – x_min – размах выборки. Если u_i > u_P,N при i=1 или i=N–1, где u_P,N – коэф­фициент, зависящий от доверительной вероятности Р и числа наблю­дений N в выборке (см. приложение), то x_minили x_max представ­ляет собой элемент выборки, содержащий грубую погрешность, и дол­жен быть удален из таблицы результатов наблюдений.

Если x_N= x_max или x₁ = x_min не содержит грубой погрешности, то проверку на наличие в выборке элементов, содержащих грубую по­грешность прекращают. В противном случае проверку повторяют, сопоставляя элемент x_N–1 с x_N–2 и, если нужно, x₂ с x₃ и т.д.

Этот же критерий можно использовать для проверки выборки на связность, сопоставляя соседние элементы упорядоченной выборки друг с другом, то есть, проверяя условия u_i > u_P,N при i=2…N–2. В случае, если выборка не является связной, эксперимент нужно повторить.

2. Другой критерий основывается на анализе отклонения экстре­мального результата наблюдения x₁ от среднего значения x. Так, если v = |x₁ – x|/S_X > v_P,N , где Sx – СКО результата наблюдения, v_P,N – коэффициенты, приведенные в приложении, то считается, что x₁ содержит грубую погрешность и его необходимо исключить из выборки.