ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА. СанктПетербургский государственный электротехнический университет Н. П. Серебрянникова б. Е. Соботковский в. В. Морозов

• Название: СанктПетербургский государственный электротехнический университет Н. П. Серебрянникова б. Е. Соботковский в. В. Морозов
• Анкор: ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА.doc
• Дата: 02.12.2017
• Размер: 1.09 Mb.
• Имя файла: ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА.doc
• Тип: Документы; #10600
• Категория: Физика
• страница: 14 из 14

3.3. Алгоритм обработки данных косвенных измерений выборочным методом

Косвенные измерения

Измерения называются косвенными, если их результат вычисляется по формулам, в которые подставляются результаты прямых измерений. Пусть нам необходимо определить значение функции F(x,y,z) от непосредственно измеренных величин x, y, z. Функция F предполагается дифференцируемой по всем переменным; кроме того, предполагается, что на интервалах, куда попадают значения x,y,z, функция F не имеет нулей частных производных. Обозначим F_i=F(x_i,y_i,z_i).

1. Выборочный метод (метод выборки)

Применяется для совместных наблюдений, т. е. в серии из N независимых опытов для каждого i величины x_i, y_i, z_i измеряются в одном опыте (при этом (x_i, i = 1..N), (y_i, i = 1..N) и (z_i, i = 1..N) выборками быть не обязаны!), причём в каждом из опытов всей серии условия для величины F одни и те же. В этом случае значения (F_i, i = 1..N) составляют выборку, по которой рассчитываются величины 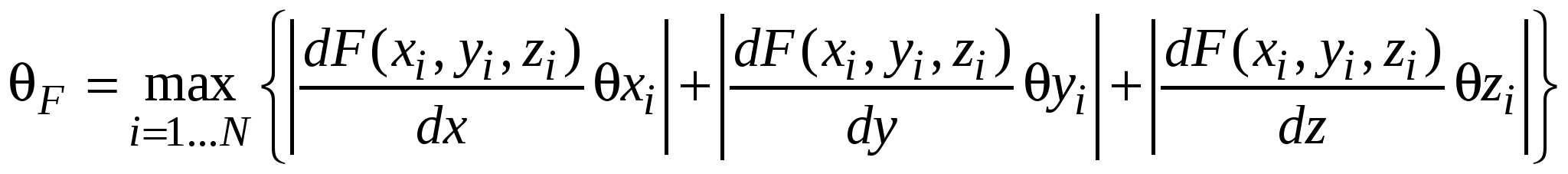и F. Приборная погрешность θ_Fрассчитывается по формуле



(предполагается, что приборные погрешности измеряемых величин могут быть разными в разных опытах) или, если F имеет удобный для логарифмирования вид, по эквивалентной формуле

.

Полная погрешность  = F + θ_F

xi									x=
yi									y=
Fi
F↑i									= , R=F↑1-F↑N=
UFi=(Fi+1-Fi)/R									P= , N= UP,N=
Fi= Fi –									Fi=0
Fi)2									Fi)2=
Fi									θF =max Fi= =

, ,

 = F + θ_F,


Приложение
Значения коэффициентов Стьюдента t_P,N в зависимости от числа наблюдений N при доверительной вероятности Р = 95%:

N	2	3	4	5	6	7	8	9	10	100
tP,N	12.7	4.3	3.2	2.8	2.6	2.5	2.4	2.3	2.3	2.0

Коэффициенты _P,N для расчета доверительной погрешности по размаху выборки x = _P,NR для числа наблюдений N доверитель­ной вероятности Р = 95%:

N	3	4	5	6	7	8	9	10	11	12
P,N	1.30	0.72	0.51	0.40	0.33	0.29	0.25	0.23	0.21	0.19

Коэффициенты u_P,N для проверки результатов наблюдений на наличие грубых погрешностей в зависимости от объема выборки N для доверительной вероятности Р = 95%:

N	3	4	5	7	10	15	20	30	100
uP,N	0.94	0.76	0.64	0.51	0.41	0.34	0.30	0.26	0.20

Коэффициенты 7р N для проверки элементов выборки на наличие грубых погрешностей в зависимости от объёма выборки N при довери­тельной вероятности Р = 95%:

N	3	4	5	6	7	8	9	10	11	12
vP,N	1.15	1.46	1.67	1.82	1.94	2.03	2.11	2.18	2.23	2.29

Производные элементарных функций:

Функция	Производная	Функция	Производная
xn	nxn-1	tg x	1 / cos2 x
eax	aeax	ctg x	-1 / sin2 x
ax	ax ln a	( u + v )’	u’ + v’
ln x	1 / x	( uv )’	u’v + uv’
sin x	cos x	( u / v )’	( u’v – uv’ ) / v2
cos x	– sin x	f = f ( u ( x ) )	f ’x = f ’u u’x