ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА. СанктПетербургский государственный электротехнический университет Н. П. Серебрянникова б. Е. Соботковский в. В. Морозов
 Скачать 1.09 Mb. Скачать 1.09 Mb.
|
2.6. Выборочные дисперсия и среднеквадратичное отклонениеДля расчета случайной доверительной погрешности результата измерений Таким наилучшим приближением или оценкой стандартного отклонения  (2.6.1) (2.6.1)называемая выборочным среднеквадратичным отклонением (СКО x) результата наблюдения от среднего. Квадрат СКО При большом числе наблюдений N – 1 N, и величина Параметр 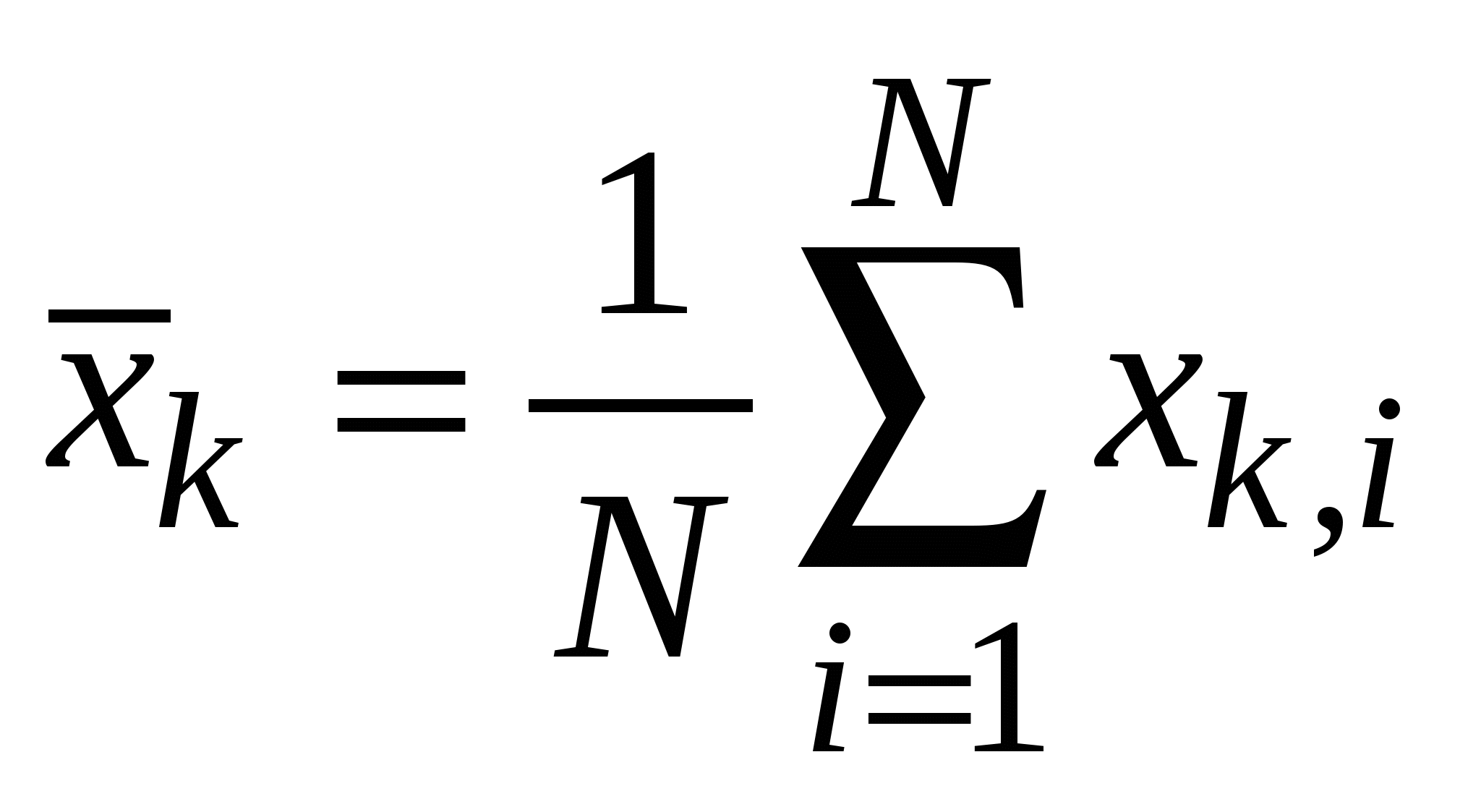 , , 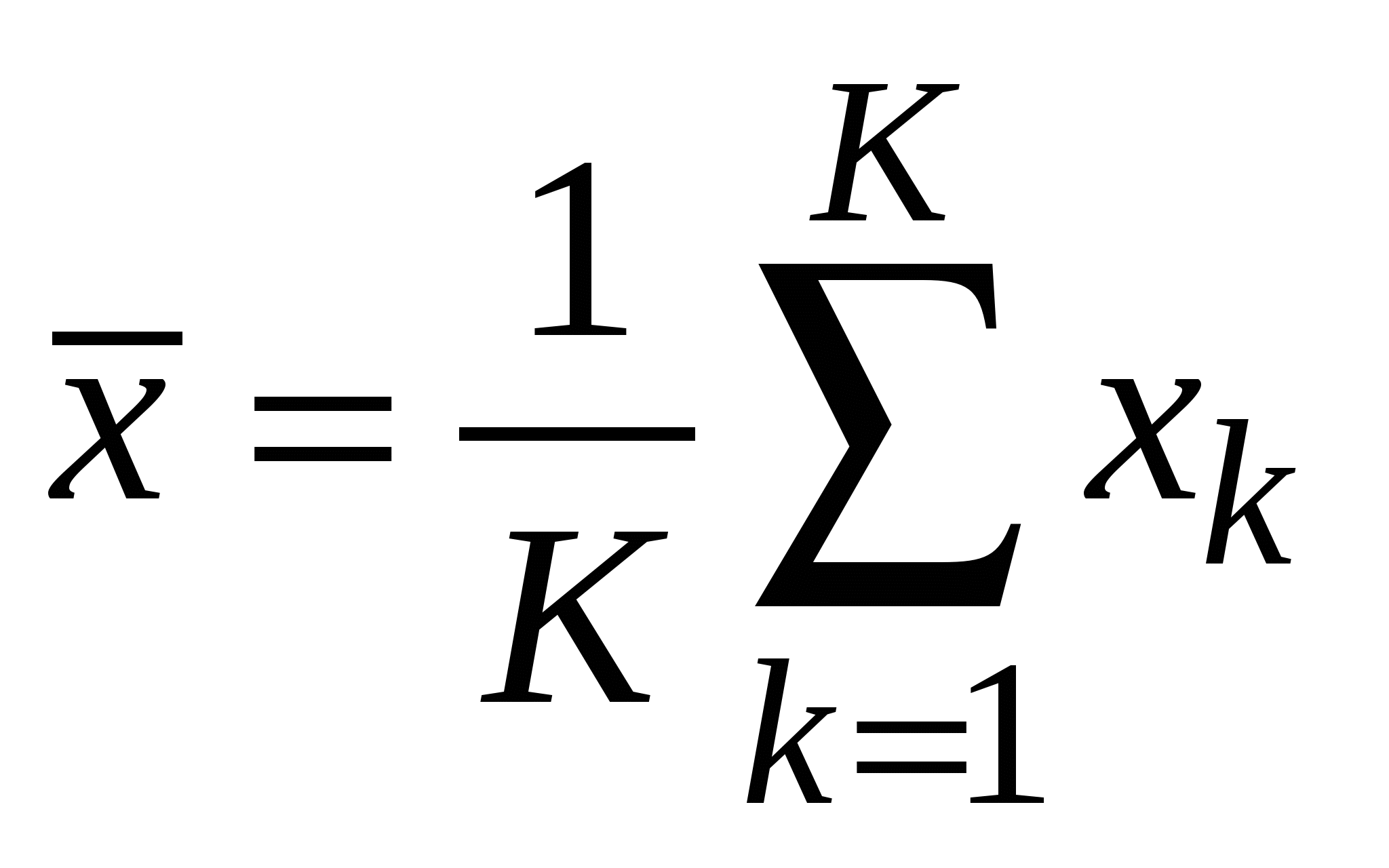 , тогда , тогда 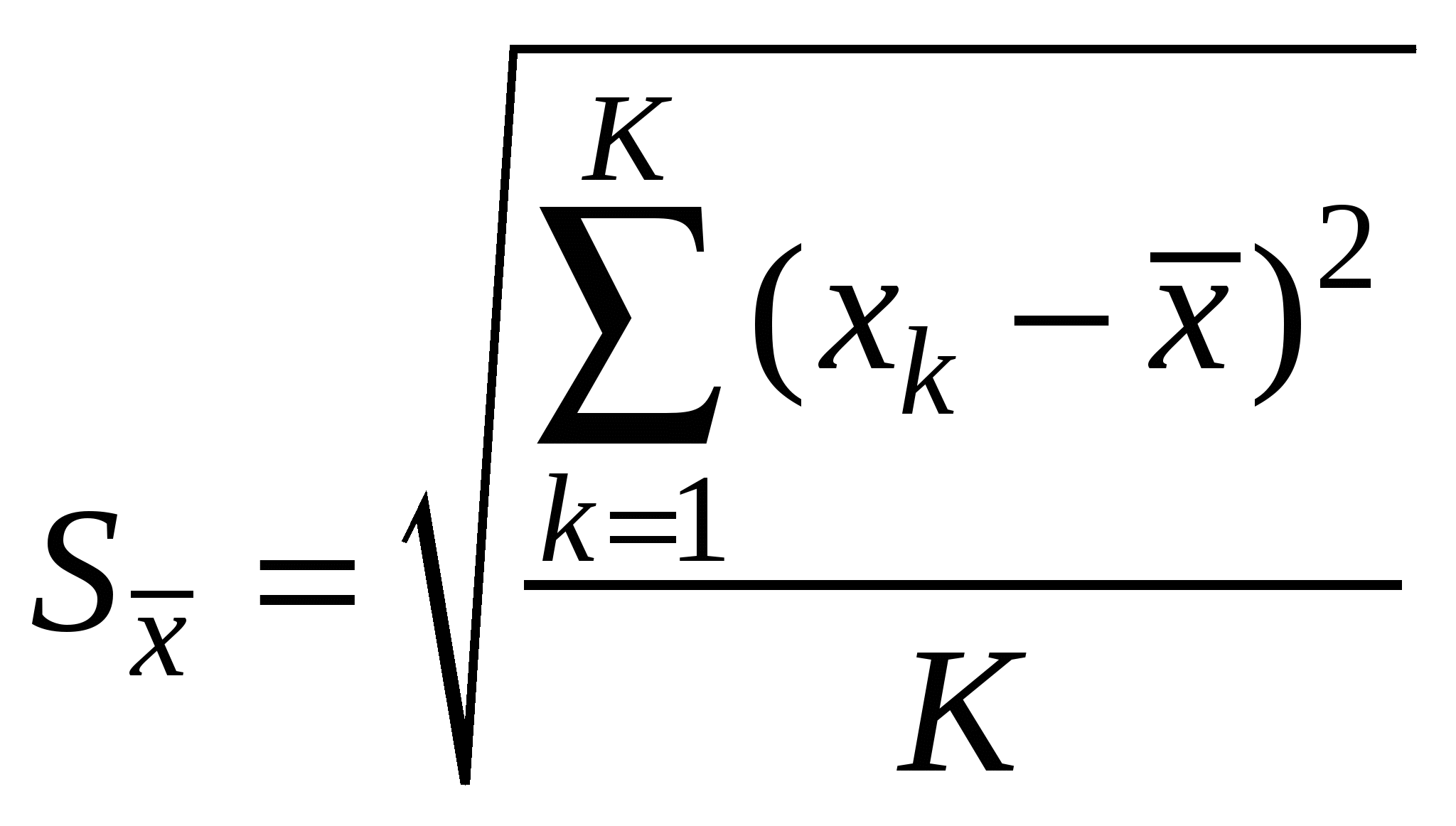 . . Можно показать, что если 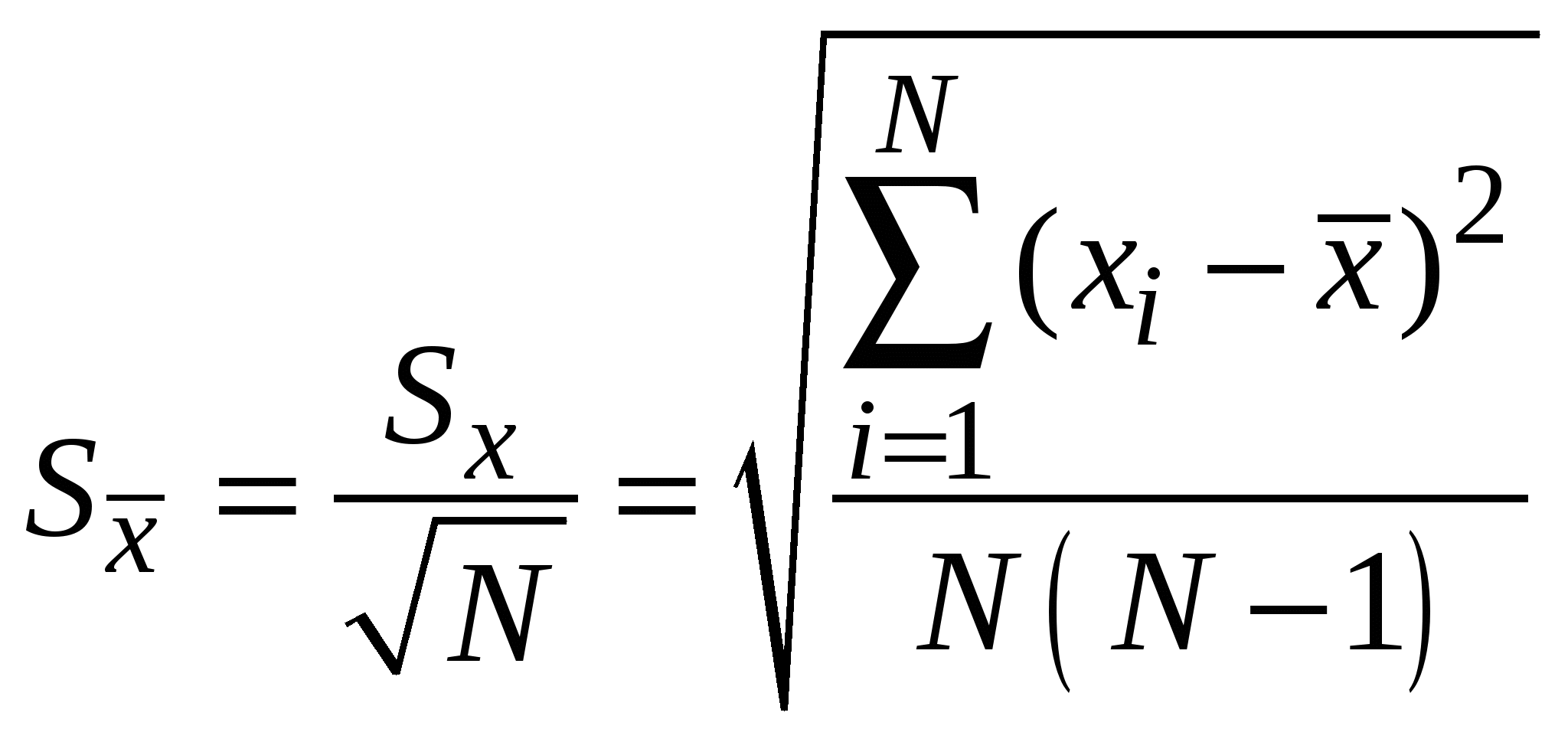 . .Если СКО где Для оценки случайной доверительной погрешности результата измерения её расчет можно производить по размаху выборки: x = P,NR, где R = xmax – xmin – размах выборки. Значения коэффициентов tP,N и P,N для данных значений доверительной вероятности (по договоренности берут значение Р = 95%) и числа N наблюдений в выборке приведены в приложении. Окончательный результат измерения записывают в виде Необходимо отметить, что при расчетах доверительной погрешности по Стьюденту результаты наблюдений должны принадлежать генеральной совокупности, распределенной по нормальному закону, что может быть проверено с помощью специальных статистических критериев. Для выполнимости этой процедуры выборка должна быть достаточно представительной (от 50 наблюдений и больше). Однако при малых объёмах выборок (N << 15), что имеет место в работах лабораторного физического практикума, проверка выборок на принадлежность нормальному распределению не производится. Как уже упоминалось в §2.4, нормальному закону подчиняются физические величины, случайность которых обусловлена действием множества независимых (или слабо зависимых) малых аддитивных факторов, результат воздействия каждого из которых мал по сравнению с их суммарным воздействием. Сюда не подходят, в частности: 1) статистика радиоактивного распада и релаксации возбуждённых состояний атомов; 2) статистика очередей в теории массового обслуживания, например, время ожидания освобождения занятого телефона. |
