ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА. СанктПетербургский государственный электротехнический университет Н. П. Серебрянникова б. Е. Соботковский в. В. Морозов

• Название: СанктПетербургский государственный электротехнический университет Н. П. Серебрянникова б. Е. Соботковский в. В. Морозов
• Анкор: ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА.doc
• Дата: 02.12.2017
• Размер: 1.09 Mb.
• Имя файла: ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА.doc
• Тип: Документы; #10600
• Категория: Физика
• страница: 9 из 14

2.11. Сложение случайной и приборной погрешностей. Полная погрешность измерения.

Пусть результаты наблюдений наряду со случайной содержат и систематическую приборную погрешность , которую можно считать по­стоянной в течение времени проведения измерения, так как характе­ристики прибора за это время не успевают заметно измениться. Наблюдаемые в опыте результаты наблюдений будут при этом равны x_i = x_i + . Наличие постоянной погрешности, вносимой прибором в результаты наблюдений, приводит к смещению выборочного среднего

.

Но ее наличие совершенно не влияет на случайную погрешность результата измерения 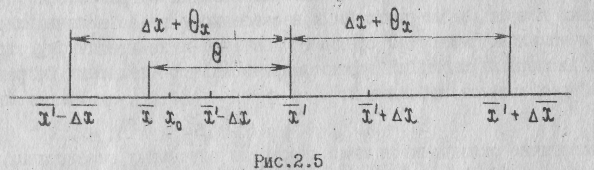, или Dx = b_P,NR, так как разности , через которые рассчитываются СКО , а также размах выборки не зависят от . Смещение среднего и доверительного интервала может привести к тому, что истинное значение x₀ из­меряемой величины окажется за пределами найденного доверительною интервала , как это показано на рис. 2.5.



Чтобы этого не произошло, надо сместить центр доверительного интервала к истинному среднему , которое является приближением кx₀. Однако ввиду неизвестности величины и знака этого сделать нельзя. Поэтому на практике параметр оценивают верхней границей возможных значений погрешностей прибора и из-за неизвестности знака истинное среднее записывают как . Тогда результат измерения можно записать в виде

,

где назовём полной погрешностью результата измерения. Новый доверительный интервал обязательно накроет истинное значение x₀, так как _x  || (рис.2.5). Отметим, что доверительная вероятность, соответствующая найденному таким образом доверительному интервалу, будет несколько превышать доверительную вероятность, используемую для нахождения случайной составляющей погрешности измерения.

В связи с этим итоговая запись результата измерения будет иметь вид

с вероятностью ,

где P₀ – вероятность определения случайной составляющей погрешности измерения.

Маловероятно, что в данном эксперименте приборная погрешность примет своё максимальное значение _x, поэтому границы нового доверительном интервала определены с запасом. Учитывая это, ГОСТ 16263-76 рекомендует определять границы доверительного интервала по формуле x = k(x + _x), где k зависит от доверитель­ной вероятности и числа наблюдений в выборке (для Р = 95% 0.7  k  0.8). Это правило основа­но на предположении, что в интервале (-_x, _x) все возможные зна­чения приборной погрешности равновероятны, т.е. приборная погреш­ность распределена равномерно. Отметим, что случайный характер приборной погрешности проявляется не в конкретном эксперименте, а в партии серийных приборов. При этом ниоткуда априори не следует, что распределение значений приборных погрешностей подчиняется равномерному закону. Оно может быть гауссовским или любым другим, а также изменяться в процессе старения приборов. При этом правила сложения приборной и случайной погрешностей также будут иными.

Установление закона распределения приборных погрешностей является процедурой очень трудоемкой и дорогой, а зачастую просто бессмысленной, так как любой результат измерения может содержать не выявленные систематические погрешности. Учитывая это, мы будем оценивать границы доверительного интервала максимальным значением . При этом мы следуем общему статистическому правилу: границы доверительного интервала лучше завысить, чем необоснованно занизить. В противном случае истинное значение x₀ может оказаться за пределами найденного доверительного интервала.