ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА. СанктПетербургский государственный электротехнический университет Н. П. Серебрянникова б. Е. Соботковский в. В. Морозов

• Название: СанктПетербургский государственный электротехнический университет Н. П. Серебрянникова б. Е. Соботковский в. В. Морозов
• Анкор: ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА.doc
• Дата: 02.12.2017
• Размер: 1.09 Mb.
• Имя файла: ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА.doc
• Тип: Документы; #10600
• Категория: Физика
• страница: 11 из 14

3. Погрешности косвенных измерений

Пусть некоторая величина f зависит от прямо измеряемых вели­чин X,У,Z,..., причём вид этой зависимости f = f(x,у,z...) изве­стен. Ввиду того, что величины x,y,z... измеряются с определенны­ми погрешностями, величина f также обладает погрешностью, которую необходимо определить. Существует два метода определения погреш­ности величины f: метод переноса погрешностей и выборочный метод.

3.1. Метод переноса погрешностей

Этот метод применяется в том случае, когда измеренные прямо величины x,y, z ..., являющиеся аргументами функции f, образуют выборки {x},{у},{z}....

Отклонения результатов отдельных наблюдений x_i, y_i, z_i… от соответствующих истинных значений x₀, у₀, z₀,... включают в себя как случайные, так и систематические составляющие. Это обстоя­тельство отмечается штрихами. Благодаря этому измеренные значе­ния аргументов обладают как случайными x, y, z..., так и систематическими приборными _(x), _(y), _(z), .... погрешнос­тями, а погрешность функции f также состоит из двух компонент: случайной f и систематической _f . Величина f определяется случайными погрешностями аргументов, а _f – систематическими при­борными.

Пусть в опыте получены выборки значений аргументов функции объема N. Тогда
i-ое значение функции f_i=f(x_i, y_i, z_i), вычисленное при смещенных значениях ее аргументов
x_i = x_i+ _(x),y_i = y_i + _(y),… можно представить в виде

где , … – смещенные средние значения аргументов функции, – случайные отклонения аргументов от их средних значений, не зависящие от постоянных приборных погрешностей _(x), _(y), _(z).

Разложим функцию f_i в окрестности точки 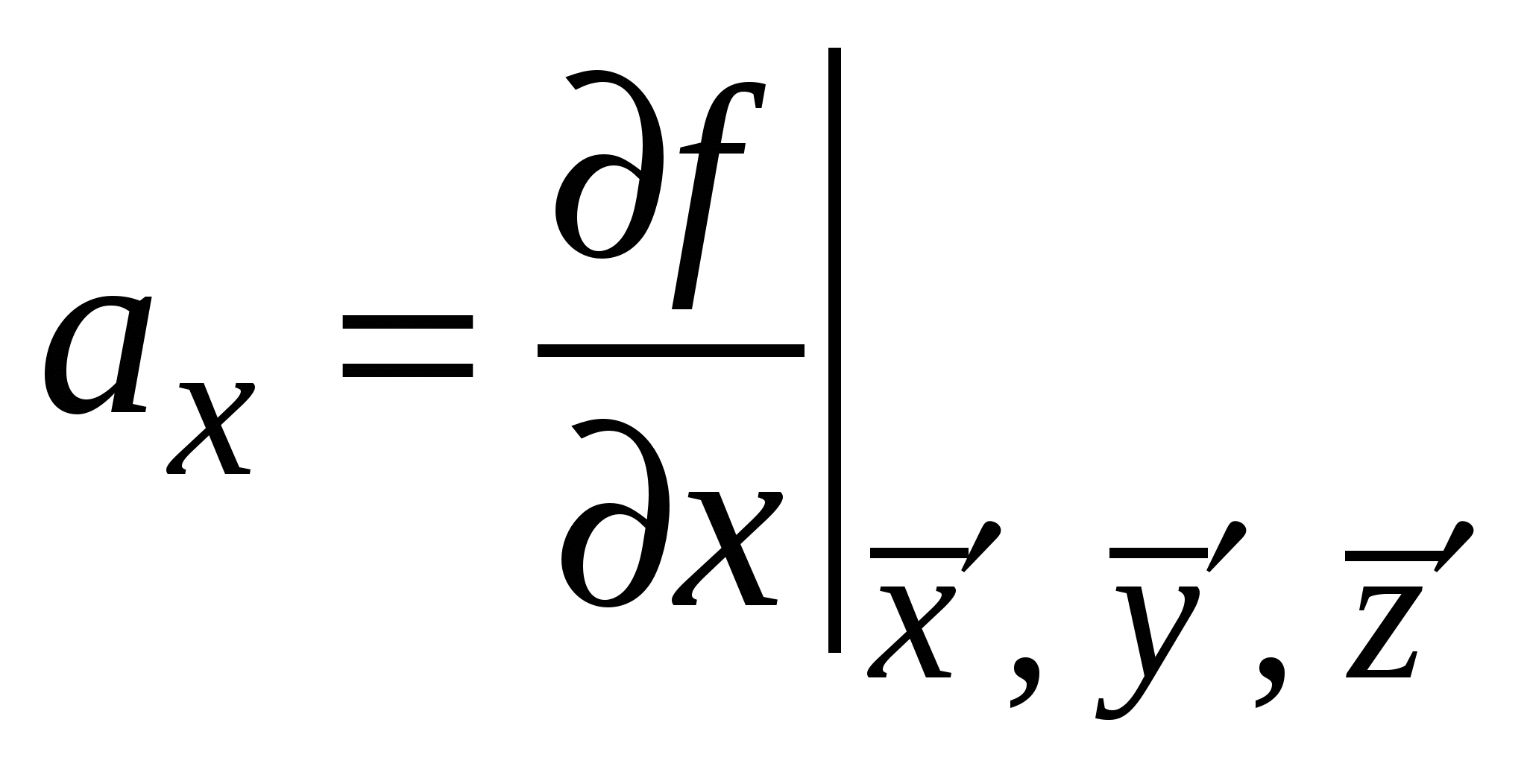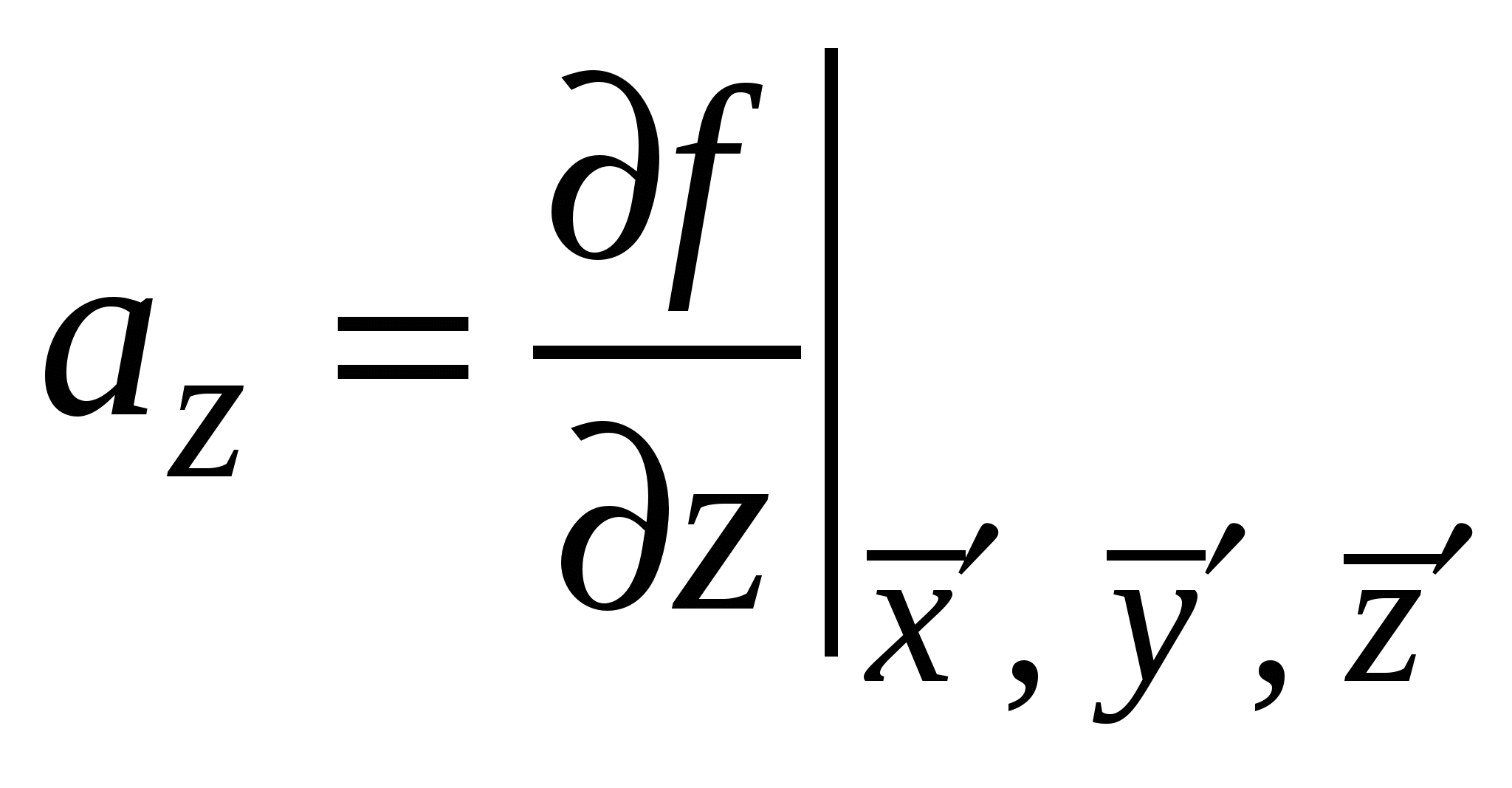в ряд Тейлора

(3.1.1)

где – среднее значение функции, вычисленное при смещенных значениях ее аргументов, – ее случайное приращение, , , …– частные производные функции, вычисленные в точке .

Рассмотрим вычисление случайной погрешности функции. Для этого вычислим дисперсию ее среднего значения. С учетом (3.1.1) получим



или



Если аргументы функции случайны и независимы, то суммы вида равны нулю. Тогда

(3.1.2)

где – дисперсии средних значений аргументов функции. Умножив обе части (3.1.2) на квадрат коэффициента Стьюдента , где N – объем выборок, по которым рассчитываются и , получим для случайной погрешности функции

,

где , , – частные случайные погрешности функции.

Смещенное среднее значение функции в (3.1.1), используя разложение в ряд Тейлора, можно выразить через ее истинное среднее

(3.1.3)

где – истинное среднее значение функции, – приборная погрешность функции. Из (3.1.3) следует, что истинное среднее значение функции, принимаемое за результат измерения, будет равно

, (3.1.4)

где ни величина, ни знак постоянных приборных погрешностей _(x), _(y), _(z) аргументов функции, а значит и , неизвестны. Приборные погрешности _(x), _(y), _(z) представляют собой независимые случайные величины. Поэтому, как и в случае случайной погрешности, для приборной составляющей погрешности функции получим

,

откуда для верхней границы приборной погрешности функции получим



где представляют собой верхние границы частных приборных погрешностей функции, а _x  |_(x)|, _y  |_(y)|, _z  |_(z)| – верхние границы аргументов функции. Коэффициенты имеют смысл весовых множителей, показывающих с каким весом случайные или приборные погрешности аргументов функции входят соответственно в случайную и приборную погрешности функции.

Оцениваемый параметр в (3.1.4) ввиду неизвестности его величины и знака лежит в пределах . С учетом этого истинное среднее значение функции

.

Результат косвенного измерения с учетом его случайной погрешности следует записать в виде



где назовем полной погрешностью функции.

Отметим следующие правила сложения погрешностей

1. 
   Случайные частные погрешности аргументов функции складываются квадратично .
   
2. 
   Верхние границы частных приборных погрешностей аргументов функции складываются квадратично .
   
3. 
   Случайная и приборная погрешности функции складываются (объединяются) в полную погрешность функции линейно .
   

Замечание. Если приборные погрешности аргументов функции не являются случайными и независимыми, например, приборная погрешность одного аргумента порождает приборную погрешность другого аргумента, то их необходимо складывать по модулю линейно .

Однако такая ситуация встречается на практике довольно редко. Она, например, может возникнуть в случае влияния работы одного прибора на показания другого, то есть наводке. В большинстве же случаев значения аргументов функции измеряются разными приборами, взаимозависимость распределения приборных погрешностей которых ниоткуда не следует. Поэтому верхние границы частных приборных погрешностей аргументов функции мы будем складывать квадратично, определяя тем самым максимальное значение верхней границы приборной погрешности функции.

Эти формулы используют в том случае, когда функция Ф удобна для логарифмирования, т.е. представляет собой произведете нескольких выражений. Операция логарифмирования как известно, превращает произведение выражений в сумму логарифмов этих выражений, а про­изводная сумма вычисляется значительно проще, чем производная произведения. Например, ln(axⁿ/(y^mtgx)) =ln a+ nlnx – mlnу- lntgx.

Окончательный результат записывается в виде

Ф = Ф’ ± Ф (3.12)

Численные значения Ф, Ф’ и Ф округляются по тем же прави­лам, которые сформулированы для прямо измеряемых величин.