ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА. СанктПетербургский государственный электротехнический университет Н. П. Серебрянникова б. Е. Соботковский в. В. Морозов
 Скачать 1.09 Mb.
|
3.2. Выборочный методВыборочный метод расчета погрешностей применяется в тех случаях, когда значения каждой из совместно измеренных величин  ,  ,  ... по отдельности не образуют выборок, но значения функции  образуют выборку, то есть величина f является некоторой физической константой, такой как ускорение свободного падения, вязкость жидкости, сопротивление проводника и т.п. Штрих у аргументов означает, что они содержат неизвестные постоянные приборные погрешности:  ,  ,  .Обработав полученную выборку значений функции с помощью стандартных приемов анализа данных прямых измерений, можно найти ее смещенное среднее значение и СКО среднего значения (либо размах выборки 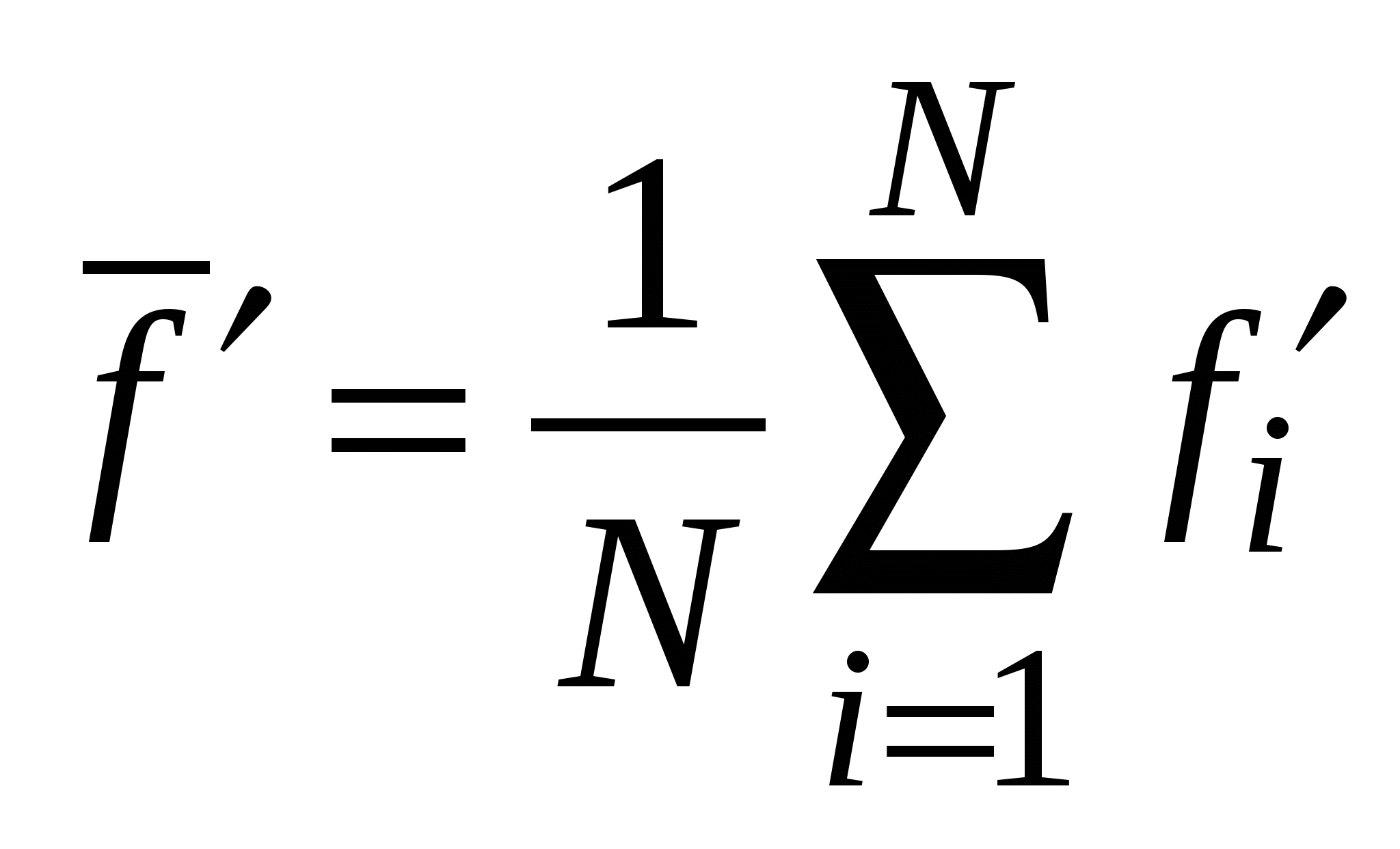 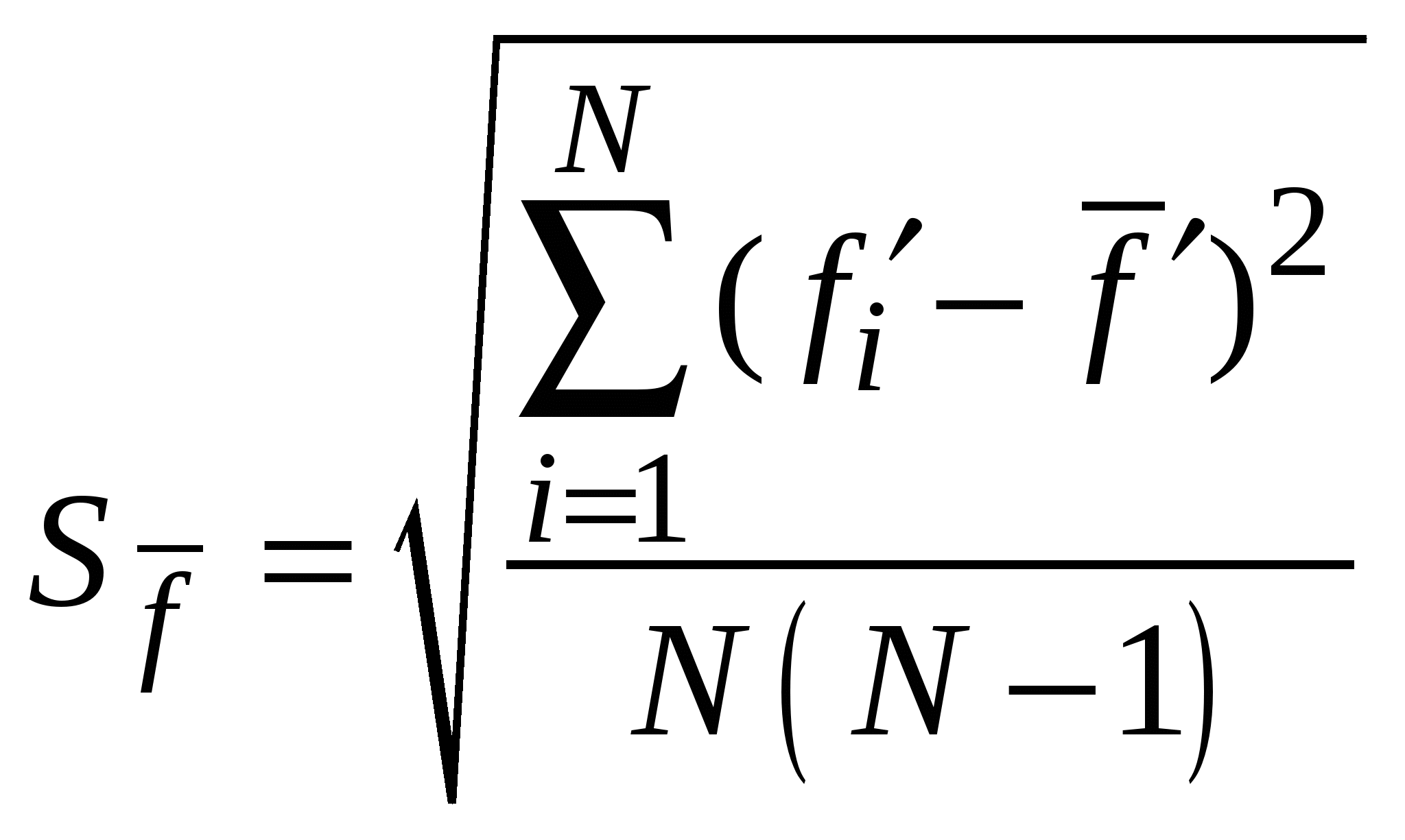)  ,  , (3.2.1) а затем вычислить ее случайную погрешность  , либо  .Для определения приборной погрешности функции разложим i-ое смещенное значение функции  в ряд Тейлора в окрестности точки  , коо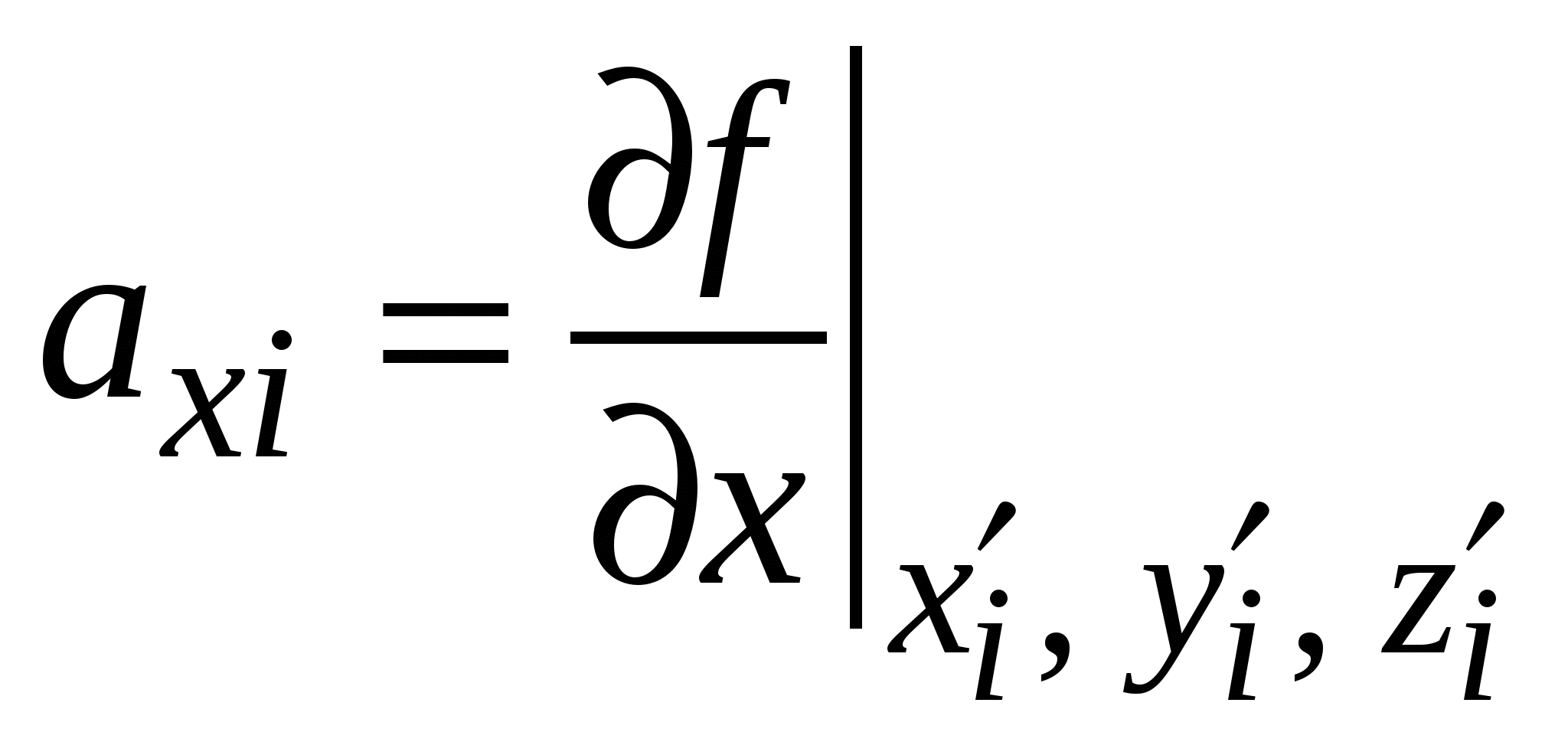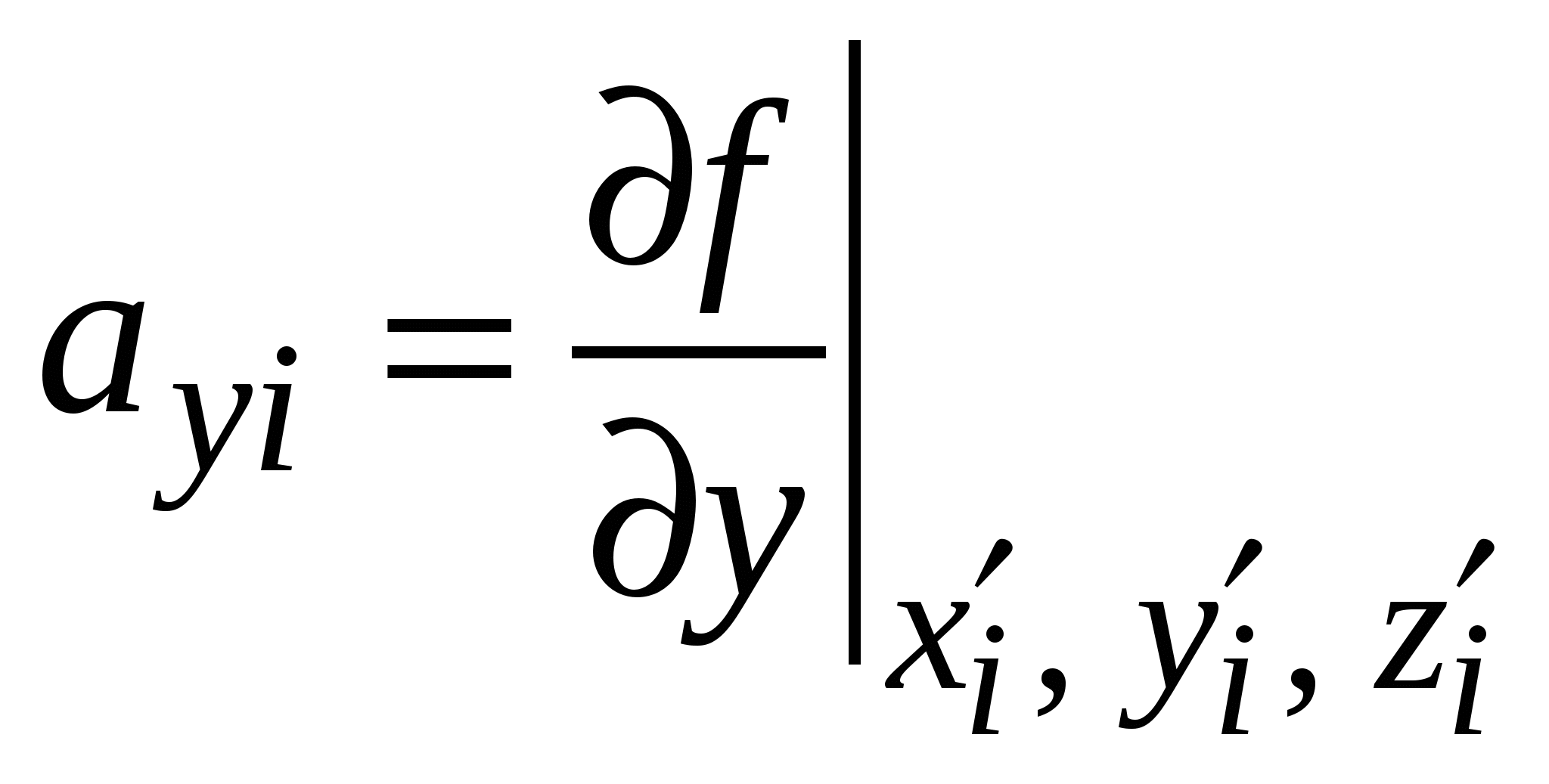рдинаты которой не зависят от приборных погрешностей:  (3.2.2)где  ,  ,  ,  .Ввиду малости приращений 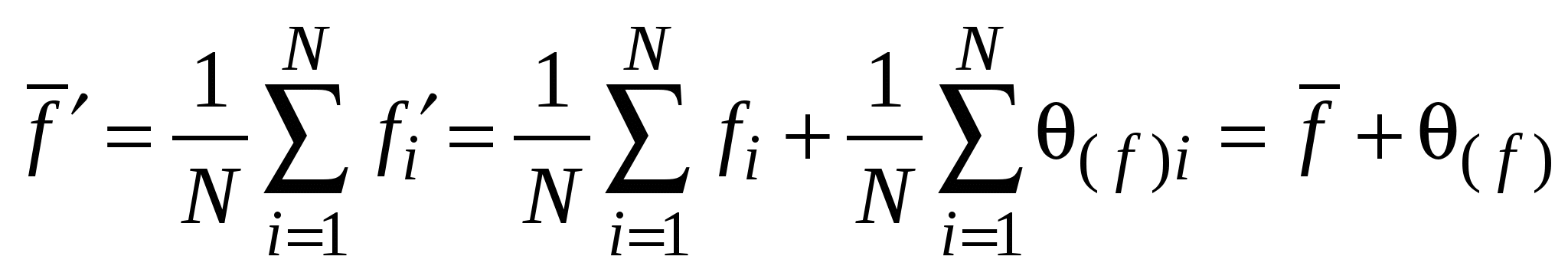 значения производных в точке можно считать совпадающими с их значениями в экспериментальной точке  . Смещенное среднее значение функции с учетом (2) будет равно (3.2.3)где  – приборная погрешность функции,  – частные приборные погрешности аргументов функции.Согласно (3) истинное среднее значение функции будет равно 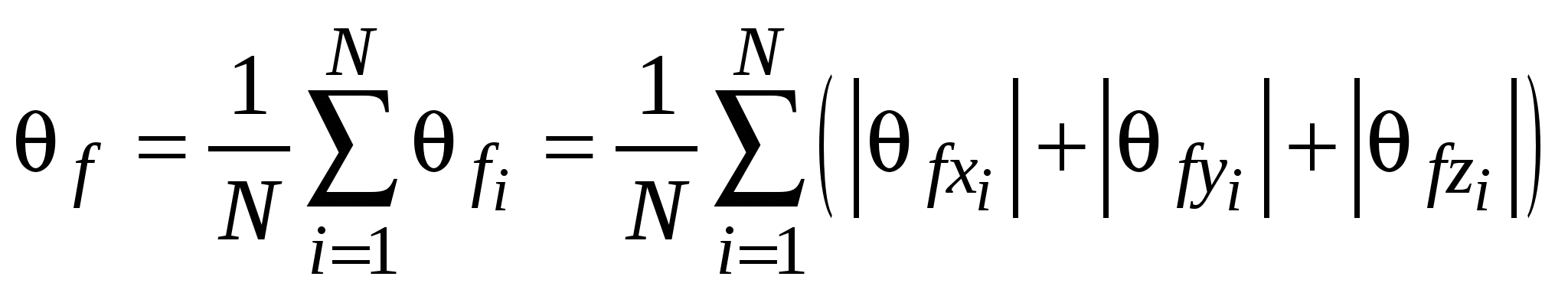 , где ввиду неизвестности величин и знаков приборных погрешностей  ,  ,  , приборная погрешность функции  также неизвестна. Поэтому заменим приборную погрешность функции ее верхней границей  . Тогда где  – верхние границы частных приборных погрешностей аргументов, вычисленные в точке .Выражение для верхней границы приборной погрешности функции функции можно также записать в виде, удобном в ряде приложений,  где  ,  ,  .Истинное среднее функции можно записать как  . Тогда результат косвенного измерения с учетом его случайной погрешности можно записать в виде ,где  – полная погрешность функции. При практических расчетах штрихи у аргументов функции и самой функции опускают. Выборочный метод допустимо использовать и в том случае, когда значения аргументов функции образуют выборки. Тем не менее, не рекомендуется применение выборочного метода к нахождению результата косвенного измерения в тех случаях, когда возможно применение метода переноса погрешностей в связи с тем, что в выборочном методе случайная погрешность функции зависит от приборных погрешностей ее аргументов, что приводит к неоправданному дополнительному увеличению погрешности функции. Действительно, случайная погрешность функции в выборочном методе рассчитывается через разности вида  в которых, ввиду большого диапазона изменения значений аргументов  и  . Заметим в заключение, что в том случае, когда функция f есть физическая константа, значение которой находится через наборы совместно измеренных значений аргументов функции выборочным методом, ее значение всегда можно найти методом наименьших квадратов (МНК), который будет рассмотрен далее. |