Антикризсное управление. Сборник задач по дисциплине антикризисное управление предприятием

• Название: Сборник задач по дисциплине антикризисное управление предприятием
• Дата: 11.11.2021
• Размер: 1.29 Mb.
• Имя файла: Антикризсное управление.doc
• Тип: Сборник задач; #269788
• страница: 16 из 24

Задача 19

Электромеханический завод в качестве конверсионной продукции разработал и организовал выпуск миксеров. Продажа миксеров была налажена в n = 6 сибирских городах: Томске, Юрге, Красноярске, Новосибирске, Кемерове и Омске. Перед началом массовых продаж во всех этих городах была проведена рекламная кампания, затраты на каждую рекламу по городам и соответствующие обороты по сбыту представлены в табл. 4.5

Таблица 4.5. Затраты на рекламу по городам

Город	Затраты на рекламу х, тыс. руб.	Оборот по продаже миксеров у, тыс. руб.
Юрга	10	140
Красноярск	20	190
Омск	20	250
Новосибирск	40	220
Кемерово	60	300
Томск	50	320

В целом в городах с большими затратами на рекламу, как правило, были и большие по размерам продажи товара. Как правило, но не везде. Можно ли в таких условиях рекомендовать заводу идти на дальнейшее увеличение затрат на рекламу? Или это сопряжено с большим риском, пустой тратой денег?

Решение. Чтобы ответить на поставленный вопрос, надо оценить тесноту связи между затратами х и результатом у. Это можно сделать с помощью коэффициента корреляции вида r_ху :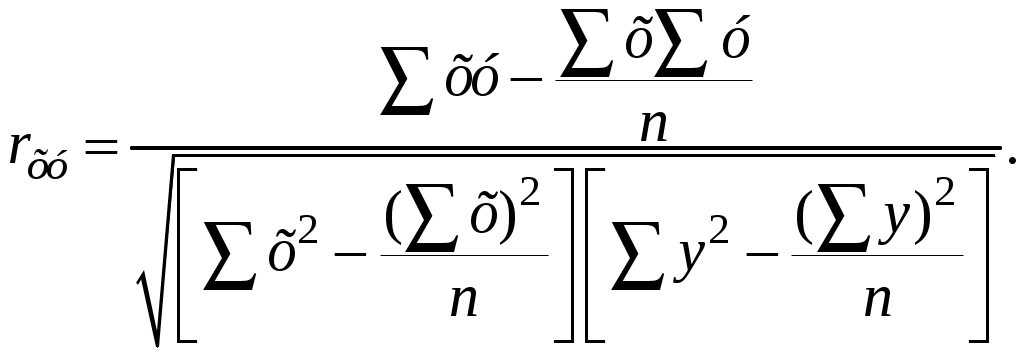



Для его исследования находим величины:

х = 200; у = 1420; ху = 53000; х² = 8600; у² = 35900.

После их подстановки в вышеприведенную формулу получим r_ху = 0,82.

Необходимо установить, насколько значимо отличается этот коэффициент от нуля. Для этого необходимо рассчитать ошибку коэффициента корреляции по формуле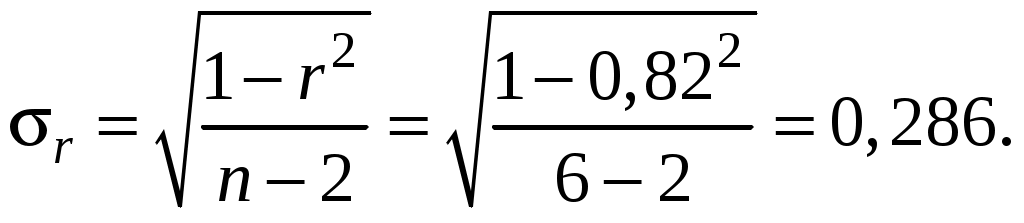



Затем с помощью рассчитанной ошибки находим значение критерия Стьюдента для разности между нулем и r_ху: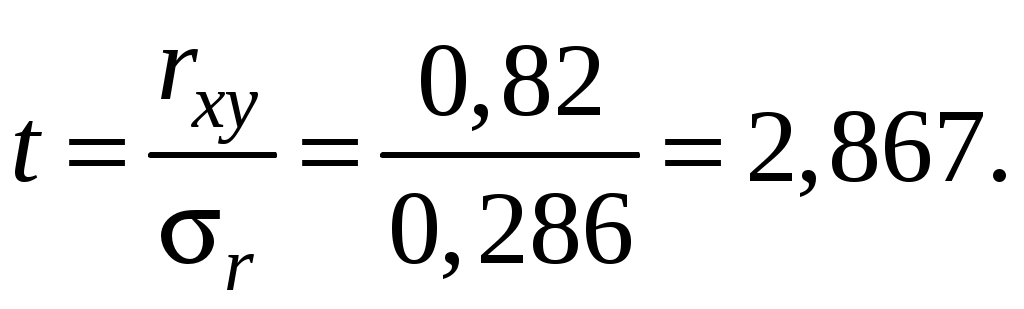



По таблицам функции распределения Стьюдента

S₄(2,8) = 0,976; S₄(2,9) = 0,978.

Следовательно, вероятность того, что коэффициент корреляции значим, равна приблизительно 0,977. Отсюда вероятность альтернативной гипотезы (для нас – это вероятность потерять деньги попусту) равна приблизительно 0,023, или 2,3%. Следовательно, надо пойти на увеличение затрат на рекламу.

9. Финансовый анализ и прогнозирование продаж в антикризисном управлении

Современное управление организациями базируется на качественно разработанных планах деятельности. В них должны быть показаны:

- цели работы в краткосрочной и долгосрочной перспективе;

- пути достижения поставленных целей;

- будущий, наиболее вероятный ход событий в работе;

- варианты будущих, наиболее целесообразных и желательных управленческих решений;

- желательные и нежелательные последствия.

Все это может быть получено по результатам прогнозирования.

Прогноз – это предвидение, выраженное в числовой форме, с указанием предположительных сроков возникновения событий. Чтобы прогноз был достоверным, необходимо использовать специальные модели и методы, например, метод выявления тенденции динамического ряда чисел или метод сглаживания ряда.

По результатам прогнозирования могут готовиться бизнес-планы, инвестиционные или инновационные планы.

Бизнес-план – это специальный инструмент управления, позволяющий запланировать, обосновать выгодность, показать гарантии и очертить круг проблем в каком-либо предпринимательском деле.

Инвестиции – капитал, который предполагается вложить в какое-либо дело.

Инновация – это нововведение (метод работы, технология изготовления или новый товар), позволяющее повысить эффективность работы организации.

Бизнес-планы, инвестиционные и инновационные планы должны быть технически и экономически обоснованы и базироваться на достоверных прогнозах развития событий, измеренных с помощью специально выбранных для этих целей показателей.

Перед осуществлением прогноза необходимо знать, как изменялся исследуемый показатель в прошлом. Исходными данными, таким образом, будет числовой ряд. В качестве чисел могут выступать: объемы продаж (ед.), курсы валют, затраты (руб.), прибыль, рентабельность работы, проценты инфляции и безработицы и т.д. Зная в прошлом изменение этих показателей, с помощью специальных методов можно будет «увидеть» наиболее вероятное их поведение в будущем. Прогнозирование может быть краткосрочным и долгосрочным.

Краткосрочное прогнозирование обычно осуществляется на один период времени вперед. В качестве периода времени может быть день, неделя, месяц, квартал, полугодие, год. Например, предприятие, торгующее скоропортящимися продуктами, заинтересовано ежедневно (или еженедельно) продавать максимум того, что можно продать. Анализируя прошлый спрос, можно осуществить прогноз на следующий период времени и сделать оптимальный по объему заказ поставщикам продукта. Дефицит, равно как и перегрузка склада с последующей порчей не купленного вовремя продукта, ведут к убыткам в работе. Объем заказа должен быть сбалансирован (без дефицита и не слишком большой) и обоснован краткосрочным прогнозом.

Другой пример. Предприятие, торгующее в больших объемах и большом ассортименте, заинтересовано в том, чтобы на складе был только тот товар и в таких объемах, который пользуется спросом. Пролеживание ненужного товара ведет к убыткам в работе, так как он занимает место другого, пользующегося спросом товара. В этой ситуации предвидение очередного спроса на весь ассортимент ведет к соответствующим заказам к увеличению товарооборота и ежедневной выручки.

Если производитель и розничный торговец выступают в одном лице, то краткосрочный прогноз спроса обусловливает также и будущий план производства товара. Соответственно для процесса производства планируются необходимые компоненты: сырье, материалы, комплектующие. Знание очередного спроса (на неделю, месяц, квартал, полугодие или год вперед) ведет к соответствующим заказам необходимых для производства средств.

Таким образом, будущий спрос влияет на всю последующую обстановку, его знание приведет к выигрышу производителя и продавца. Как же получить это знание? Оказывается можно. Осуществить краткосрочный прогноз спроса на очередной период времени можно с помощью специальных процедур.

Один из примеров таких процедур – процедуры сглаживания. Они преследуют одну цель: по данному изменяющемуся числовому ряду построить другой числовой ряд, сохраняющий его динамику, но имеющий значительно меньшее колебание своих членов и показывающий тенденцию их изменения.

Например, известно, что прошлые объемы продаж (в тыс. шт.) за 12 месяцев были следующими:

2, 10, 4, 8, 6, 14, 8, 18, 10, 24, 12, 30.

Можно вычислить средние для пар близлежащих величин и построить новый ряд, состоящий уже из 11 членов:

(2 + 10)/2 = 6;

(10 + 4)/2 = 7;

(4 + 8)/2 = 6;

(8 + 6)/2 = 7;

(6 +14)/2 = 10;

(14 + 8)/2=11;

(8 + 18)/2 = 13;

(18 + 10)/2 = 14;

(10 + 24)/2 = 17;

(24 + 12)/2 = 18;

(12 + 30)/2 = 21.

Построив графически зависимости объемов продаж во времени для исходного и вычисленного усредненного ряда, можно увидеть недостатки метода. Они очевидны: во-первых, при сглаживании ряд укорачивается, а прогнозирование требует продолжения ряда; во-вторых, все члены ряда учитываются при усреднении с одинаковыми весами, а при прогнозировании последние члены ряда должны иметь больший вес, чем ранние. Вес члена ряда – это уровень его значимости во времени. Очевидно, что более поздние члены ряда значимее для анализа и выводов, чем ранние. Показанный метод усреднения ряда имеет ограниченное применение. Им целесообразнее пользоваться не в краткосрочном, а в долгосрочном прогнозировании, когда необходимо выявить только тенденцию изменения величин.

Показанные недостатки устраняются при использовании другого метода выравнивания ряда, – метода экспоненциального сглаживания. Это наиболее эффективный способ разработки краткосрочного прогноза спроса на товары, продающиеся в большом количестве и ассортименте.

Пример краткосрочного прогнозирования

Рассмотрим пример расчета экспоненциальной средней для 10 периодов времени (столбец 1 табл. 1.1). Каждый период может, например, представлять месяц (4 недели) или другой интервал, соответствующий допущениям о времени реализации (продажам) товара. Фактический спрос в течение этих периодов (в единицах измерения отдельных видов товаров) показан в столбце 2.

Таблица 1.1  Данные для прогнозирования

Коэффициент сглаживания а = 0.2 (В скобках показаны номера столбцов)

Период вре­мени	Фактиче­ский спрос на конец пе­риода, усл. ед.	Взвешенный фактический спрос (2) х 02	Взвешенный старый про­гноз (5) х 08	Прогноз на будущий пе­риод (3) + (4)	Ошибка прогноза
1	2	3	4	5	6
Предыдущий 1	80	16	56	70 72	–10
2	90	18	58	76	–18
3	110	22	61	83	–34
4	95	19	66	85	–12
5	105	21	68	89	–30
6	120	24	71	95	–10
7	105	21	76	97	–20
8	130	26	78	104	–33
9	125	25	83	108	–21
10	135	27	86	113	–27
Итого	1095	219	703	922	215
Среднее	ПО	22	70	92	22

Предположим, что период 1 только что завершен с фактическим спросом на продажу (объемом продаж) 80 ед. Теперь необходимо спрогнозировать спрос на следующий период.

Текущий спрос имеет определенное отношение к предсказанию будущего, при этом он связан и с прошлым. В частности, в период, непосредственно предшествующий только что завершившемуся, прогнозная оценка составила 70 ед. (см. столбец 5 табл. 1.1). Разница, как видно, составляет 10 ед.

Сглаживая известный числовой ряд продаж товара ломаной кривой, мы можем приближаться к динамике фактических продаж, обеспечивая резкие скачки величин (если фактические продажи имеют явно выраженные резкие скачки), или, наоборот, обеспечивать большую плавность перехода от одной величины к другой. Уровень сглаживания измеряется через специальный коэффициента.

Зададим для данного примера коэффициент сглаживания а = 0,2. Соответственно Р = 1 – а характеризует значимость старого прогноза.

Прогноз на будущий период будет равен:

Новый прогноз = а*фактический спрос + Р*старый прогноз.

Произведем расчет для нашего примера.

На конец периода 1 фактические продажи равны 80 усл. ед., а старый прогноз был 70 усл. ед. (см. табл. 1.1). Следовательно, значение прогноза на будущий второй период равно:

0.2 х 80 + 0.8 х 70 = 72 усл. ед.

Так как предшествующий старый прогноз был 70 усл. ед., а фактические продажи были 80 усл. ед., то ошибка прогноза в первом периоде равна минус 10 (см. столбец 6 табл. 1.1).

На конец периода 2 фактические продажи равны 90 усл. ед., а старый прогноз составил 72 усл. ед. Следовательно, значение нового прогноза на будущий третий период равно:

0.2 х 90 + 0.8 х 72 = 76 усл. ед.

Соответственно, ошибка прогноза во втором периоде составляет:

72 – 90 = – 18 усл. ед.

Аналогично вычисляются значения прогнозов и для других периодов. Вся информация сводится в табл. 1.1

Данные таблицы представлены графически на рис. 1.1.

Р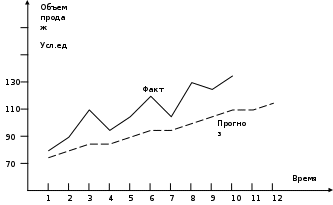
ис. 1.1  Фактические и прогнозные продажи при а = 0.2
Этот график показывает, что сделанный прогноз является неточным: явно видно, что фактические продажи намного больше, чем предполагалось.

Как же оценить или измерить достоверность прогноза? Оказывается, можно. Для измерения ошибки прогнозирования вводится показатель – среднее абсолютное отклонение (САО). Оно вычисляется как сумма всех ошибок прогнозов по периодам, деленная на количество периодов. При этом ошибки прогнозов для каждого из периодов берутся без учета знаков. Действительно, нам безразлично, имеет ли ошибка знак «+» или «–».

Например, для а = 0.2 суммируются все ошибки столбца 6 табл. 1.1. В результате получим значение 215. Разделим 215 на количество периодов. Получим округленное САО равное 22.

Очевидно, чем меньше САО, тем точнее прогноз. Зададим теперь вопрос: не даст ли нам новый коэффициент сглаживания лучший прогноз? Чтобы ответить на него, пересчитаем табл. 1.1 для другого коэффициента сглаживания, например, а = 0.4. В результате получатся новые значения прогнозных оценок и новое САО (табл. 1.2). Видно, что прогноз улучшился, САО стало равно 14.

Таблица 1.2  Данные для прогнозирования

Коэффициент сглаживания а = 0.4

1	2	3	4	5	6
				(70)
1	80	32	42	74	–10
2	90	36	44	80	–16
3	110	44	48	92	–30
4	95	38	55	93	–3
5	105	42	56	98	–22
6	120	48	59	107	–22
7	105	42	64	106	+2
8	130	52	64	116	–24
9	125	50	70	120	–9
10	135	54	72	126	–15
Итого	1095	438	574	1012	143
Среднее	110	44	57	101	14

Увеличим еще коэффициент сглаживания, сделаем его а = 0.6. Peзультаты улучшатся, САО станет равно 13 (табл. 1.3).

Таблица 1.3  Данные для прогнозирования

Коэффициент сглаживания а = 0.6

1	2	3	4	5	6
				(70)
1	80	48	28	76	–10
2	90	54	30	84	–14
3	110	66	34	100	–26
4	95	57	40	97	+5
5	105	63	39	102	–8
6	120	72	41	113	–18
7	105	63	45	108	+8
8	130	78	43	121	–22
9	125	75	48	123	–4
10	135	81	49	130	–12
Итого	1095	657	397	1054	127
Среднее	ПО	66	40	105	13

При а = 0.8 результаты сглаживания и прогнозирования будут наилучшими, а САО минимальным – 12 (табл. 1.4).

Таблица 1.4  Данные для прогнозирования

Коэффициент сглаживания а = 0.8

1	2	3	4	5	6
				(70)
1	80	64	14	78	–10
2	90	72	16	88	–12
3	110	88	17	105	–22
4	95	76	21	97	+ 10
5	105	84	19	103	–8
6	120	96	21	117	–17
7	105	84	23	110	+ 12
8	130	104	21	112	–23
9	125	100	25	112	0
10	135	108	25	113	–10
Итого	1095	876	202	1078	124
Среднее	110	88	20	108	12

Результаты прогнозирования с а = 0, 8 показаны на рис. 1.2.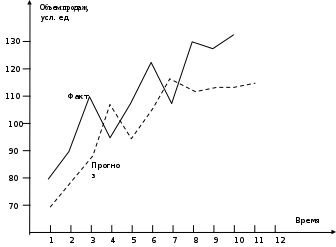


Рис. 1.2  Фактические и прогнозные продажи при а = 0.8

По сравнению с рис. 1.1 этот вариант прогнозирования является оптимальным для рассматриваемых десяти периодов времени. В случае продолжения слежения за рядом (после десятого периода) для оптимального прогнозирования может возникнуть необходимость выбора другого значения а, при котором САО будет минимальным.

На практике все приведенные в таблицах расчеты по сглаживанию проводит ЭВМ. То, что мы проделали вручную, заполняя таблицы, делает машина. После каждого периода времени она анализирует фактический ряд данных, рассчитывает все САО для коэффициентов а от 0.1 до 1 (с шагом 01), находит оптимальный коэффициент сглаживания для этого ряда (чтобы САО было минимальное) и сама делает прогноз на следующий период. Метод проб и ошибок в данной процедуре не допустим.

Опыт краткосрочного прогнозирования показал, что для спроса с резкими подъемами и спадами оптимальный сглаживающий коэффициент будет высоким (от 0.5 до 0.9), а для относительно плавных рядов коэффициент от 0.1 до 0.2 может оказаться наилучшим.

Пример долгосрочного прогнозирования

Если краткосрочное (по неделям, месяцам, кварталам) прогнозирование помогало предвидеть одно следующее за рядом событие, при этом мы пытались смотреть на «один шаг» вперед, то при долгосрочном прогнозировании можно увидеть общую тенденцию (тренд или «поведение») процесса на много шагов вперед. В этом состоит отличие этих методов.

Долгосрочное прогнозирование является полезным инструментом стратегического планирования в менеджменте. Осуществляя достоверный прогноз продаж в будущем, можно заранее запланировать и подготовить необходимые материальные ресурсы, производственное оборудование, склады, каналы поставок и сбыта произведенной продукции.

Рассмотрим пример. Новый товар продавался фирмой последние семь лет, и ежегодный объем продаж увеличился со 1000 до 9000 единиц за этот период. На первый взгляд, рассматривая график продаж на рис. 1.3, можно оптимистично предсказать объем в 11000 ед. на следующий год и 13500 ед. на следующий за ним год. Такой прогноз основан на первом впечатлении, но на самом деле тенденция изменения продаж менее оптимистична. Докажем это.

В первую очередь мы должны найти общую тенденцию (тренд) изменения объема продаж. Она может быть линейно увеличивающейся, линейно уменьшающейся или не изменяющейся, постоянной. Необходимо построить эту линию.

Методика построения.

1. Заносим все известные объемы продаж за семь лет в табл. 1.5 (столбцы 1 и 2); в сумме они составляют 35 тыс единиц.

2. В столбце 3 указываем, на сколько удален каждый рассматриваемый год от центрального четвертого года. Очевидно, что третий год удален от четвертого на минус 1, второй год на минус 2, первый год – на минус 3. Соответственно, пятый год удален от четвертого на плюс 1, шестой год – на плюс 2, а последний седьмой – на плюс 3.

3. Умножаем данные продаж столбца 2 на величину удаления годов от центрального (столбец 3). Полученные результаты заносим в столбец 4. Например, в первом году значение продаж 1, величина удаления первого года от центрального равна минус 3; перемножая эти данные, получим значение минус 3 и т.д.

4. Возведем отклонения годов от центрального в квадраты и занесем полученные значения в столбец 5.

5. Вычислим с учетом знаков сумму всех величин столбцов 4 и 5, в результате получим 26 и 28.

6. Разделим сумму четвертого столбца на сумму пятого, получим:

26 / 28 = 0.929.

Округленно будем считать, что данное отношение равно 1. Это отношение показывает уровень наклона линии. Если это отношение положительно (как в данном примере), то и наклон линии положительный, она идет по восходящей слева направо. Если отношение отрицательно, то линия идет по нисходящей.

7. Нарисуем эту линию на графике. Для этого возьмем объемы продаж в четвертом центральном году (5 тыс. ед.):

5x1 = 5 тыс. ед.

Получили первую точку линии. Отметим ее на графике (рис. 1.3).

Далее, будем от центрального четвертого года вправо каждый раз прибавлять к рассчитанным объемам продаж величину наклона, а от центрального четвертого года влево отнимать от рассчитанных объемов продаж величину наклона. В случае, если отношение наклона отрицательно, то необходимо, наоборот, от центрального года вправо отнимать величину наклона, а влево – прибавлять ее.

Для данного примера получим следующие объемы продаж:

- для пятого года: 5+1 = 6 тыс. ед.;

- для шестого: 6+1=7 тыс. ед.;

- для седьмого: 7+1 = 8 тыс. ед;

- для третьего: 5–1=4 тыс. ед;

- для второго: 4–1 = 3 тыс. ед;

- для первого года: 3–1=2 тыс. ед.

Отметим эти точки на графике и соединим их. Получилась наклонная линия, которая показывает общую тенденцию динамики продаж. Она называется трендом.

Продлевая ее за пределы семилетнего периода, получим долгосрочный прогноз объемов продаж:

- для восьмого года: 8+1=9 тыс. ед.;

- для девятого года: 9 + 1 = 10 тыс. ед.;

- для десятого года: 10+1 = 11 тыс. ед.

Необходимо заметить, что точность (достоверность) такого прогноза зависит от двух очень важных факторов: сохранения условий работы, сложившихся за прошлые года (в данном примере семь лет), и от величины рассматриваемой базы прогнозирования. Очевидно, что чем больше количество исследуемых величин (база прогнозирования), тем точнее прогноз.

Контрольные задачи