Антикризсное управление. Сборник задач по дисциплине антикризисное управление предприятием

• Название: Сборник задач по дисциплине антикризисное управление предприятием
• Дата: 11.11.2021
• Размер: 1.29 Mb.
• Имя файла: Антикризсное управление.doc
• Тип: Сборник задач; #269788
• страница: 13 из 24

8. Принятие управленческих решений в антикризисном менеджменте на основе статистических гипотез

Кризисные явления на инновационном предприятии могут обостриться из-за снижения выручки от инновационных проектов, из-за ошибочных управленческих решений, которые привели к чрезмерным затратам.

В ряде случаев это обусловлено тем, что приходится принимать управленческие решения на основе тех или иных предположений из-за отсутствия достаточно полной и достоверной информации. Чтобы избежать потерь, надо при первой возможности проверять истинность предположений. Этого можно достичь с помощью приемов проверки статистических гипотез, которые носят универсальный характер, так как в виде статистической гипотезы можно подать почти любое предположение из области бизнеса и экономики. Проверки гипотез позволяют по относительно небольшим выборкам, требующим незначительных затрат труда и средств, предупреждать потери от вложения средств в бесполезные мероприятия.

Приемы проверки заключаются в исследовании следующих гипотез:

– гипотезы о выборочных средних: генеральная дисперсия известна;

– гипотезы на основе выборочной средней: генеральная дисперсия неизвестна;

– гипотезы на основе выборочной доли;

– гипотезы о двух генеральных дисперсиях;

– гипотезы о форме распределения;

– гипотезы о связи между двумя переменными.

При проверке гипотез различают нулевую и конкурирующую (альтернативную) гипотезы. Для проверки первой существуют специальные таблицы. Судьба же второй решается на основании результатов проверки нулевой: если принимается нулевая, то отклоняется конкурирующая.

Техника проверки гипотез сводится к расчету фактических значений специальных критериев и сравнению их с табличными значениями для определения уровня значимости. По общему правилу нулевая гипотеза отклоняется в пользу конкурирующей тогда, когда К_факт>К_табл для Q, где К – общий символ любого критерия, Q – заданный уровень значимости проверки, который является одним из входов в таблице значений соответствующих критериев.

При решении многих прикладных задач из области экономики вполне достаточным считается 5-процентный уровень значимости проверки, он гарантирует от потерь при принятии рискованных решений.

Рассмотрим некоторые приемы проверки гипотез на следующих примерах.

Задача 14

Центр профессиональной переподготовки при ТУСУРе (университет, обучающий проектированию наукоемкой продукции) проводит платные курсы повышения квалификации по четырем специальностям. Продолжительность курсов два месяца; в год осуществляется четыре набора. На протяжении последних трех лет (12 наборов) среднее общее количество слушателей в каждом наборе М было 20 человек со стандартным отклонением , равным 3. С целью расширения набора принимается решение добавить еще две специальности. Последующие два набора (n= 2) показали, что среднее число слушателей выросло до m_ср = 23 человека. Необходимо определить, обусловлен ли этот рост введением новых специальностей или определяется случайным разбросом набора, не претерпевшего изменений. Если выяснится, что расширение набора произошло за счет инновации (введения новых специальностей), то центр тогда приступит к разработке и выпуску учебных пособий по этим специальностям, начнется освоение дистанционного образования.

Решение. Можно предполагать, что распределение слушателей по наборам подчиняется нормальному распределению, так как количество слушателей зависит от многих обстоятельств (цена, покупательная способность населения, наличие нескольких альтернативных курсов, программа курсов, их продолжительность и качество, рейтинг вуза и т.д.).

Нулевая гипотеза Н₀ состоит в том, что выборочная средняя m_ср согласуется с нормальной генеральной совокупностью со средней М, то есть увеличение слушателей не зависит от наличия двух новых специальностей, а произошло просто их перераспределение по шести специальностям.

Альтернативная гипотеза Н₁ состоит в том, что выборка по последним двум наборам взята не из нормального распределения со средней, равной 20 человек. Следовательно, рост слушателей до 23 человек был обусловлен введением двух дополнительных специальностей.

Проверим нулевую гипотезу при 5-процентном уровне значимости, используя распределение с одной границей (рис. 4.5).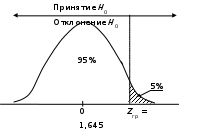



Рис. 4.5. Граничное значение для уровня значимости 5%

Используя стандартное нормальное Z-преобразование для р = 0,95, из таблиц интеграла вероятностей находим Z_гр = 1,645.

Рассчитаем проверочную статистику Z_пр: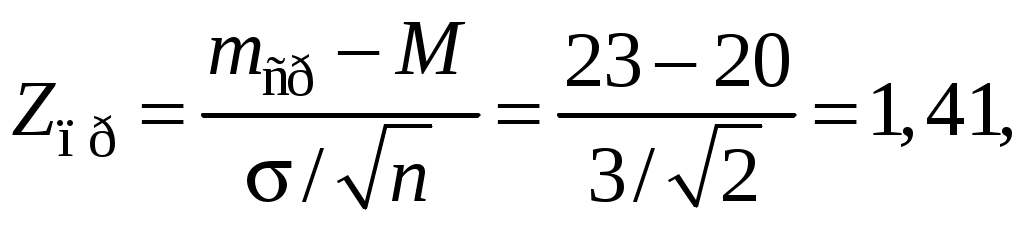



где n – количество последующих наборов, равное 2.

Так как Z_пр < Z_гр, делаем вывод о принятии нулевой гипотезы и отклонении первой Н₁, то есть увеличение числа слушателей объясняется простым разбросом случайной величины – набора слушателей генеральной совокупности. Следовательно, нет необходимости производить больших затрат на выпуск пособий по новым специальностям. Если бы набор увеличился до 25 человек за последующие два набора, уже можно было бы решать вопрос в пользу альтернативной (первой) гипотезы, или если бы набор в 23 человека был бы средним не за два, а за четыре последующих набора, также можно было бы рискнуть в пользу первой гипотезы. Учитывая последнее, имеет смысл понаблюдать за величиной набора еще полгода и затем уже принять окончательное решение.